深入理解計算機系統第三版家庭作業答案-第二章
2.55-2.57答案:
show_bytes 原始碼:
#include<stdio.h> typedef unsigned char* byte_pointer; void show_bytes(byte_pointer ch, int len){ printf("show bytes:"); for (int i = 0; i < len; i++) printf ("%.2x ", ch[i]); printf("\n"); } void show_short(short x) { show_bytes((byte_pointer) &x,sizeof(short )); } void show_long(long x) { show_bytes((byte_pointer) &x,sizeof(long )); } void show_double(double x) { show_bytes((byte_pointer) &x,sizeof(double )); } int main() { int x = 1; short y = 32767; long z = 32767; double d = 3.14; printf("linux:\nshow number: %d %d %ld %f\n",x,y,z,d); show_bytes((byte_pointer) &x,sizeof(int )); show_short(y); show_long(z); show_double(d); return 0; }
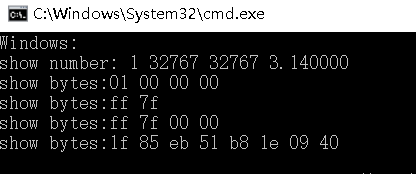
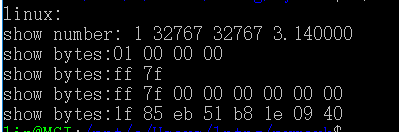
執行結果:
沒有sum,windows10和linuxubuntu上執行結果都是小端位元組序。
2.58
小端位元組序下int x=1位元組序為01 00 00 00
大端位元組序下int x=1位元組序為00 00 00 01
將其強制轉換為char*型別返回第一個位元組即可判斷是小端還是大端
程式碼如下:
typedef unsigned char* byte_pointer;
int is_little_endian()
{
int x = 1;
return *((byte_pointer) &x);
}
注意資料型別都是轉換為unsigned char* 而不是char*,這兩個是會導致不同的輸出結果。
2.59
int a = 0x89ABCDEF;
int b = 0x76543210;
printf("%02x\n",(a&0xFF)|(b&0xFFFFFF00));你也可以用不同的演算法,我知道int是32位4位元組故使用0xFFFFFF00,不知道下可以用~0xff來表示結果一樣。
2.60
unsigned replace_byte(unsigned x,int i,unsigned char b)
{
i=i*8;
return (x&~(0xFF<<i)|(b<<i));
}2.61
程式碼如下:
#include<stdio.h> int YESORNO(int x) { return ( (!x) | (!(~x)) | (!(0xff&(~(x&0xff)))) | (!(x>>((sizeof(int)-1)<<3))) ); } int main() { int x; for(;;) { scanf("%x",&x); printf("%d\n",YESORNO(x)); } return 0; }
!x判斷全為0情況
!(~x)判斷全為1情況
(!(x>>((sizeof(int)-1)<<3)))判斷最高位元組位全為0情況,sizeof(int)32機子為4,x實際右移24位也就是將最高位元組位移到最低位元組位
(!(0xff&(~(x&0xff))))
先將x和0xff相與消除其他位的影響,取反後再相與,如果沒有相與的話假設情況為0x000000ff那麼取反後值為0x0xffffff00,多出來的幾位ffffff將影響判斷,故應該和0xff相與僅保留最低位元組位,我們是判斷最低位元組為全1的情況。
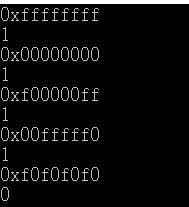
執行結果:
2.62
int_shifts_are_arithmetic()
{
int x=-1;
return (x>>1)==-1;
}特殊情況-1位元組序為0xffffffff 算術右移填充符號位1故值不變;邏輯右移填充0數值改變不為-1。
2.63
原始碼:
#include<stdio.h>
unsigned srl(unsigned x,int k)
{
unsigned xsra = (int) x >> k;
return (xsra&(~(-1<<(8*sizeof(int)-k))));
}
int sra(int x,int k)
{
int xsrl = (unsigned) x >> k;
int flag=(xsrl&(1<<(8*sizeof(int)-k-1)));
if(flag)//填充1
return (xsrl|(-1<<(8*sizeof(int)-k)));
else
return xsrl;
}
int main()
{
int x1,k;
for(;;)
{
scanf("%x %d",&x1,&k);
unsigned x2=unsigned(x1);
printf("邏輯右移:%02x>>%d -->%02x\n",x2,k,srl(x2,k));
printf("算術右移:%02x>>%d -->%02x\n",x1,k,sra(x1,k));
}
return 0;
}執行結果:
2.64
x的32位bit中奇數位為1時候返回1,否則返回0原始碼:
int any_odd_one(unsigned x)
{
return x & 0x55555555;
}2.65
x的32位bit包含奇數個1時候返回1否則返回0,原始碼:
int odd_ones(unsigned x)
{
int count=0;
for(int i=0;i<sizeof(unsigned)*8;i++)
if ((x>>i)&0x1)
count++;
return count;
}看到最多包含12個算術運算覺得上面程式碼不符合,只能通過每位異或得到結果。
程式碼如下:
int any_ones(unsigned x){
x ^= (x >> 16);
x ^= (x >> 8);
x ^= (x >> 4);
x ^= (x >> 2);
x ^= (x >> 1);
return !(x&1);
} 2.66
說白了就是通過只保留最左邊的那個1得到的數字,事例 0xff00-->0x8000,由上題思路和提示得到類似思路,將x最左邊的1開始的後面的全部位變為1,如0x0100-->0x01ff,然後將其右移一位再和x異或來清除原始碼:
int leftmost_one(unsigned x)
{
x |= (x >> 1);
x |= (x >> 2);
x |= (x >> 4);
x |= (x >> 8);
x |= (x >> 16);
return x^(x>>1);
}2.67
A問題出在1<<32
B只要排除大於32位情況就可以,既然不能移動32那麼移動31次就好了,我們把1自己先左移一位變成2不就好了,改成2<<31即可這種方法返回結果是正確但是同樣會警告忽略即可。
C加一個判斷16位情況即可,程式碼:
int bad_int_size_is_32()
{
int before_msb = 0x2 << 15;
int set_msb = before_msb << 15;
int beyond_msb = set_msb<<1;
return before_msb && set_msb && !beyond_msb;
}以上程式碼在至少32位機器不會警告,但是16位機器會警告。
2.68
函式功能:輸入n,輸出位元位最右邊為n個1的數字,原始碼:
int lower_ones_mask(int n)
{
return (0x1<<n)-1;
}2.69
實現迴圈左移,程式碼:
int rotate_left(unsigned x,int n)
{
unsigned y=x>>(32-n);
x = x << n;
return (x|y);
}2.70
函式功能,輸入x,n,判斷x是否可以用n位位元數來表示,說白就是,前w-n+1位必須全是1或全是0,加的是n位位元數的符號位,原始碼:
int fits_bits(int x,int n)
{
x=x>>(n-1);
return !x || !(~x);
}2.71
書上翻譯太垃圾了,看了半天才知道要幹嘛,首先有一個unsigned型別的數記為word 它由四位元組組成,要求我們寫個函式實現提取指定的單個位元組出來,比如word為0x12345678,那麼bytenum為0(0-3)時取出來0x78,然後,記得還沒完,那位前任之所以被解僱就是因為沒有然後,要將提取出來的數字轉為有符號數,程式碼如下:
int xbyte(unsigned word ,int bytenum)
{
int y=word<<((3-bytenum)<<3);//將要提取的位元組移到最高位
bytenum=sizeof(int)<<3;
return y>>bytenum;//用有符號數的算術右移來實現,無符號轉有符號
}2.72
A:int轉換為unsigned型別所以很小的時候比如int=-1會被轉換為Umax,所以還是會判斷成功
B 程式碼如下:
if(maxbytes >= sizeof(val) && maxbytes > 0)2.73
實現飽和加法,正溢位返回Tmax,負溢位返回Tmin,分別取x,y,sum的符號位填充到head_,接著判斷head_x和head_y全為1而head_sum為0時候是負溢位,head_x和head_y全為0且head_sum全為1時候是正溢位,其餘情況不溢位,故程式碼如下:
int saturating_add(int x,int y)
{
int Tmax=0x7fffffff;
int Tmin=0x80000000;
int sum=x+y;
int head_x=x>>31;
int head_y=y>>31;
int head_sum=sum>>31;
int flag_tmin=head_x&head_y&(~head_sum);
int flag_tmax=(~head_x)&(~head_y)&head_sum;
int flag_sum=~(falg_tmin|flag_tmax);
return sum&(flag_sum) | Tmax&(flag_tmax) | Tmin&(flag_tmin);
}2.74
程式碼如下:
int tsub_ok(int x,int y)
{
int sub=x-y;
if( (x>=0 && y<0 && sub<x) || (x<0 && y>=0 && sub>y) )
return 0;
else return 1;
}2.75
要做這題必須走一遍乘法運算過程才好理解,假設w=4時候計算過程如圖:
程式碼如下:
int add_out(unsigned x, unsigned y)
{
return x + y >= x;
}
unsigned unsigned_high_prod(unsigned x, unsigned y)
{
int w = sizeof(int)<<3;
unsigned high = 0;
unsigned sum = (y&0x1)?x:0;
for(int i=1; i<w; i++)
{
if( (y>>i) & 0x1 )
{
high += x>>(w-i);
if(!add_out(sum, x<<i)) high++;
sum += (x<<i);
}
}
return high;
}2.76
calloc函式程式碼:(可以自己在庫函式找原始碼)
void *calloc(size_t nmemb ,size_t size)
{
unsigned long nsize=nmemb*size;
char *s;
if(nmemb==0 || size==0 || nsize>0xffff) return NULL;
else
{
s=malloc(nsize);
memset(s,0,(unsigned)nsize);
return s;
}
}2.77
A:x*17=x<<4+x;
B:x*(-7)=x*(1-8)=x-x<<3;
C:x*60=x*(64-4)=x<<6-x<<2;
D:x*(-112)=x*(16-126)=x<<4-x<<7;
2.78
正確的舍入方式應該是向零舍入,要求x/(2^k),知道x為正數時候就是向零取整,但是x為負數時候就是向下取整不合理,故使用下面表示式:
(x<0 ? x+(1<<k)-1 : x) >> k;即可求得正確答案
2.79
求3*x/4;原式子可化為(x<<1+x)>>2,可以轉換為x>>2+x>>1+低二位進位?1:0,比如x為0001bit位,那麼要判斷,01(x原來的低二位)和10(x左移一位後的低二位)是否有進位,如果有再加1;程式碼如下:
int mul3div4(int x) // 3*x/4
{
int cf=(((x<<1) & 0x3)+(x & 0x3)) >> 2;
return (x>>2)+(x>>1)+cf;
}2.80
以題目意思應該是求3/(4x),而不是3/4*x那樣跟上題一樣還有什麼意思,思路差不多,當x為正數時候不考慮,當x為負數的時候,為了向上舍入,需要偏量4x-1,故程式碼如下:
x<0?(3+4*x-1)/(4*x):3/(4*x)2.81
A:(~0)<<k
B:((1<<k)-1)<<j
2.82
A:但x為Tmin時候,-x也為Tmin故等式兩邊不想等
B:數學推到如下:
17*y+15x=16(x+y)+y-x=(x+y)<<4+y-x;C:同A,x為0x80000000時候會導致錯誤
D:無符號和有符號位級操作一樣
E:先右移不存在溢位,然後再左移回來可知道只可能由於低二位的丟失造成數值變小故小於等於原值
2.83
A:題意:比如y=(01)那麼Y=1,k=2,我們要求的是0.010101...值為多少,設為x,提示知道,x*2^k=Y+x-->x=Y/(2^k-1),
B由A公式便可計算得到.
2.84
ux<=uy ^ (sy | sx)
六種情況:
ux<=uy 為1時候,有三種
1.sx=0,sy=0,則返回1,因為都是正數
2.sx=0,sy=1,則返回0,因為y為負數,x為正數,必然是x>y;
3.sx=1,sy=1,則返回0,因為xy都為負數,絕對值小的反而大;
ux<=uy為0時候,有三種:
1.sx=0,sy=0,則返回0
2.sx=1,sy=0,則返回1,因為x為正數,y為負數,必然x<y
3.sx=1,sy=1,則返回1,因為,xy都是負數,那麼絕對值數值大的x反而小.
2.85
A:7.0 --> 111.0--> 1.11 -->E=2,M=1.11 ,f=0.11,V=7.0 e=2+2^k-1
B:最大奇整數:m=1.1111...1,E=n,f=0.111...1,V=M*2^n
C:最小規格化數的倒數,最小規格化數是V=2^(-2^(k-1)+2),則1/V=2^(2^(k-1)-2),,則E=2^(k-1)-2,M=1,f=0.00;
參考課本p82
2.86
最小正非規格化數 0 | 0,,,0 | 0 | 0....01 非規格化E=1-bias=2-2^14,m=2^(-63),V=m*2^E 具體10進位制自己按計算器可得
最小正規化數 0 | 0....1| 1 | 000..00 E=e-bias=2-2^14,m=1
最大規格化 0 | 111..0| 1 | 11...11 E=2^14-1 m=1.111..11
2.87
描述 hex M E V D
-0 0x8000 0 -15
最小的>2的值 0x4001 1025/1024 1 1025*2^(-9) 2.00195315(手機計算器得到)
512 0x6000 1 9
最大非規格數 0x03ff 1023/1024 -14 1023*2^(-24) 0.000060975516
負無窮大 0xfc00
0x3BB0 0x7376 955/512 13 955*2^(4) 15280
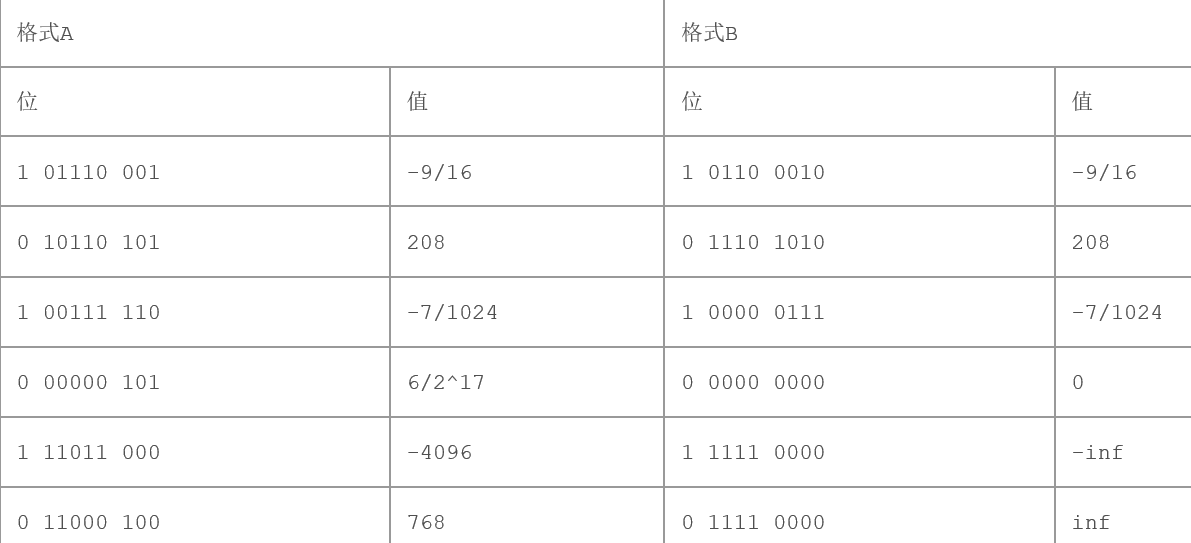
2.88
2.89
A 錯,因為Float表示證書低於double,Tmax float就表示不了,而double可以
B錯誤,因為x-y溢位時候,double不會溢位
C正確,都是正數不存在舍入問題,故可以用加法結合律
D乘法可能導致溢位問題,,比如,dx與dy相乘造成溢位,與dy和dz相乘造成的溢位不同,就會得到不同的結果.
E錯誤,其中一個為0,另一個不為0時候
2.90
frac是低23位表示,exp是高9位表示,參考課本p82 圖2-36
if (x<-149)
{
exp =0;
frac=0;
}
else if (x<-126)
{
exp =0;
frac=1<<(x+149);
}
else if (x<128)
{
exp =x+127;
frac=0;
}
else
{
exp =255;
frac=0;
}2.91
A11.0010 0100 0011 1111 0110 11
B根據提示對照公式x=Y/(2^k-1),得到k=3,Y=001 22/7=3+1/7
故表示為11.001001001...
C第九位
2.92
float_bits float_negate(float_bits f)
{
if( (f&0x7fffff) && ((f>>23) & 0xff) == 0xff )
return f;
else
return f^0x8000000000;
}2.93
float_bits float_absval(float_bits f)
{
if( (f&0x7fffff) && ((f>>23) & 0xff) == 0xff) )
return f;
else
return f&0x7fffffffff;
}2.94
float_bits float_twice(float_bits f)
{
unsigned sign=f>>31;
unsigned exp=(f>>23) & 0xff;
unsigned frac=f&0x7fffff;
if( exp == 0xff )
return f;
else if(exp==0)//非規格
return (sign<<31) | (frac<<1);
else if(exp<254)//規格
return (sign<<31) | ((exp+1)<<23) | (frac);
else//無窮大
return (sign<<31) | (0xff<<23);
}2.95
偶數舍入,判斷最後兩位,01,00 10舍掉,11則加一位.
float_bits float_half(float_bits f)
{
unsigned sign=f>>31;
unsigned exp=(f>>23) & 0xff;
unsigned frac=f&0x7fffff;
if( exp == 0xff )
return f;
else if(exp==0)//非規格
return (sign<<31) | ((frac>>1)+(1 & (frac&3==3)));
else if(exp==1)//規格
return (sign<<31) | ((exp-1)<<23) | ( (frac>>1)&0x400000);
else
return (sign<<31) | ((exp-1)<<23) | frac;
}2.96
int float_f2i(float_bits f)
{
unsigned sign=f>>31;
unsigned exp=(f>>23) & 0xff;
unsigned frac=f&0x7fffff;
if( exp=0xff )
return 0x80000000;
else if(exp<127)//小於1的
return 0;
else if(exp>149)
frac = (0x800000^frac)<<(exp-149);
else
frac = (0x800000^frac)>>(149-exp);
return sign? -frac :frac;
}2.97
float_bits float_i2f(int i)
{
if(i==0) return 0;
unsigned x=i>0? i:-i;
unsigned exp=127;
unsigned sign =i&0x80000000;
unsigned frac=0;
int k;
unsigned mask;
for(k=0;k<32;k++)
if(x>>k==1) break;
exp+=k;
if(k<=23)
frac=x<<(23-k);
else{
frac = x>>(k-23);
mask=(0xffffffff>>(55-k));
if( (x&mask) == 1<<(k-24) )
frac += ( (x>>(k-23)) & 1);//為一半時候 進位取為要保留位最低位值;
else if( (x&mask) > 1<<(k-24))
frac++;
if(frac==(1<<24)) exp++;
}
return sign | (exp<<23) | (frac&0x7fffff);
}參考課本p86,關於強制轉換原則,int轉float不會溢位.
相關推薦
深入理解計算機系統第三版家庭作業答案-第二章
2.55-2.57答案:show_bytes 原始碼:#include<stdio.h> typedef unsigned char* byte_pointer; void show_bytes(byte_pointer ch, int len){ prin
[第五章] 深入理解計算機系統第三版 家庭作業參考答案
5.13 A. 畫圖: 關鍵路徑為第三幅圖加粗部分 B. 下界為浮點加法的延遲界限,CPE 為 3.00 C. 整數加法的延遲界限,CPE 為 1.00 D. 關鍵路徑上只有浮點加法 5.14 v
[第八章] 深入理解計算機系統第三版 家庭作業參考答案
8.9 程序對 併發麼? AB × AC √ AD √ BC √ BD √ CD √ 8.10 A. fork B. longjmp execve C. setjmp 8.11 4次,畫畫程序圖就行了 8.12 8次
[第三章] 深入理解計算機系統第三版 家庭作業參考答案
人非聖賢孰能無過,歡迎大家提問與糾錯 3.58 long decode2(long x, long y, long z) { y -= z; x *= y; return ((y << 63) >> 63) ^ x; } 3.5
[第六章] 深入理解計算機系統第三版 家庭作業參考答案
6.22 磁軌數 d 與 r - x * r 成正比 設 d = k(r - x * r) = kr(1 - x) 總容量 c = 2πxk(r^2)(1 - x) = 2πk(r^2)(x - x^2) 上式實際上是關於 x 的二次式,其對稱軸為 1/2,即當
《深入理解計算機系統第三版》第三章家庭作業參考答案
簡述 最近看docker和k8s的底層實現原理,嚴重感覺自己對底層的知識瞭解不足,於是開始業餘時間深入看一些底層書籍,就找了本據說是理解整個計算機體系的入門書-《深入理解計算機系統》.直接買的最新的第三版,從第三章開始看的,第二章接下來有心情再看(看了幾眼全是
深入理解計算機系統 第三版 第三章 家庭作業 答案
3.58long decode2(long x,long y,long z) { int ret; y=y-z; x=x*y; ret=y; ret<<=63; ret>>=63; return ret^x; }算術左移63再右移6
<深入理解計算機系統(第三版)》第一章
第一章 計算機系統漫遊 計算機系統是由硬體和系統軟體組成的,它們共同工作來執行應用程式. 1.1 資訊就是位+上下文 源程式實際上就是由一個值0和1組成的位(bit)序列,8個位被組織成一組,稱為位元組.每個位元組表示程式中某個文字字元. 大部分現代系統都是有ASCII標準表示文字字元,只由ASCII字
深入理解計算機系統 第三章大略和第五章大略
$0 一個 編譯 存儲器 系統 32位 做了 ++i 擴展 這2章總結的很少,主要是覺得沒那麽重要。 1.2個操作數的指令,第二個操作數通常是目的操作數:movb a b,move a to b,而add a b,b+=a,指令分為指令類,如mov類:movb,movw,m
深入理解計算機系統 第三章 程式的機器級表示 part1
如題所示,這一章講解了程式在機器中是怎樣表示的,主要講組合語言與機器語言。 學習什麼,為什麼學,以及學了之後有什麼用 我們不用學習如何建立機器級的程式碼,但是我們要能夠閱讀和理解機器級的程式碼。 雖然現代的優化編譯器能夠很有效的將高階程式碼翻譯成機器級的程式碼,但是,為了
深入理解計算機系統 第三章 程式的機器級表示 part2
這周由於時間和精力有限,只讀一小節:3.4.4 壓入和彈出棧資料 棧是一種特殊的資料結構,遵循“後進先出”的原則,可以用陣列實現,總是從陣列的一端插入和刪除元素,這一端被稱為棧頂。 棧有兩個常用指令: push:把資料壓入棧中 pop:刪除資
深入理解計算機系統 第三章 程式的機器級表示 part3
這周看了劉老師提供的相關視訊,以及書中對應的章節“3.7 過程” 這一節分為執行時棧、轉移控制、資料傳送、棧上的區域性儲存、暫存器中的區域性儲存空間和遞迴過程這 6 個小節 其中前 3 小節看懂了一部分內容,後面兩個還沒來得及看,下週看完補上
深入理解計算機系統 ——第三章 程式的機器級表示
### 這一章主要是介紹高階語言,例如C語言編寫的程式,經過編譯後轉換為彙編程式。以往在程式設計師對機器進行操作主要都是使用匯編語言。筆者在大學做微控制器開發的時候,老師制訂的實驗,明確要求使用匯編語言。 組合語言的使用和掌握能夠很好地幫助程式設
《深入理解計算機系統》(原書第三版)家庭作業第三章(3.63)解答
原題目: **3.63 虛擬碼分析:x rdi ;n rsi n=n-0x3c(60); if(n>5){-->4005c3 } else{ goto:*(8n+0x4006f8)
深入理解計算機系統第十二章學習筆記
應用級併發應用情況:訪問慢速I/O裝置;與人互動;通過推遲工作以降低延遲;服務多個網路客戶端;在多核機器上進行併發計算。 三種基本構造併發程式的方法:程序、I/O多路複用、執行緒 1、基於程序的併發程式設計 例如構建一個併發伺服器: 假設有1個伺服器和2個客戶端,伺服器正在監聽lis
深入理解計算機系統 第六章 儲存器層次結構
為什麼要學習儲存器的層次結構? 如果我們理解了系統是如何將資料在儲存器層次結構中上上下下移動的,那麼我們就可以編寫自己的應用程式,使得它們的資料項儲存在層次結構較高的地方,在那裡 CPU 能更快地訪問到它們。 區域性性原理 計算機程式傾向於引用臨近於其他最近引用過的資料項
深入理解計算機系統——第六章
有一個 圖片 組成 技術分享 data- 計算機 系統 大量 src 存儲器 磁盤 磁盤可以存儲大量的數據,但是速度慢 磁盤由盤片組成,每個盤片有兩面,上面覆蓋著磁性記錄材料,盤片中央有一個可以旋轉的主軸 深入理解計算機系統——第六章
深入理解計算機系統--第七章課後作業
對於問題一,輸出結果如下圖所示: 兩個都是弱定義值,所以連結器隨機選擇一個,而這時在c2.c中,g的值為37(強定義),故c1.c的g為37,呼叫函式f,g變為38 當執行第二條語句時,結果如圖: 多次定義變數g,程式在連結的時候報錯!!! 對
深入理解計算機系統----第九章虛擬記憶體
原文連結 https://www.jianshu.com/p/e1b82b230917 虛擬儲存器又叫做虛擬記憶體,我們現在的作業系統普遍都支援了虛擬記憶體,這樣做是因為我們同時執行著太多的程式了,就目前我電腦的狀態來看,我既要開啟瀏覽器,又要聽歌,可能同時還登陸的有QQ,如果不使用虛擬記
深入理解計算機系統----第八章異常控制流
原文連結 https://www.jianshu.com/p/c8a6c4154219 目 錄 每次從一條指令過渡到另外一條指令的過程稱為控制轉移,這樣的一個控制轉移序列叫做控制流,如果每條指令都是相鄰的,這樣的過渡就是平滑序列。如果一條指令與另外一條指令不相鄰,這樣突發性