本部落格中概率圖模型（Probabilistic Graphical Model）系列筆記以 Stanford 教授 Daphne Koller 的公開課 Probabilistic Graphical Model 為主線，結合資料（每篇博文腳註都附有連結）加以補充. 博文的章節編號與課程視訊編號一致，詳情見 PGM（概率圖模型）Coursera: 課程資源分享和簡介.
　　筆記持續更新，為便於對照課程查閱，博文中章節編號和名稱與課程視訊的編號和名稱一致.

1. Welcome

　　生活中很多工需要人活自動系統推理完，即利用合適的資訊去獲取結論。例如， 醫生需要了解患者的資訊一一症狀、化驗結果、個性特徵——並對可能的疾病和採用的治療方案做出結論。概率圖模型屬於機器學習一種，能夠使計算機系統完成上述型別的任務。

2. Overview and Introduction

2.1 動機

2.1.1 陳述性表示 ( Declarative Representa tion )

 　　面對一個問題，我們通常會先用陳述性表示（Declarative Representation）形式化**這個問題，從而極大地方便了對問題的求解。

• 使得我們可以通過構建模型描述客觀世界中的複雜問題，並對其進行推理。

  　　同一的型別問題可以採用通用形式的模型框架，不同的模型又有通用的演算法求解。這使得我們在求解問題時可以靈活選擇將問題歸為哪一類問題，從而建立相應的模型；同時我們可以選擇不同的演算法，在準確性和計算成本之間作權衡

  （trade-offs bewteen accuracy and computational cost）。

• 一個關鍵特性是模型和推理的分離。

  　　陳述性表示本身有清晰的語義(stands for itself)，並與求解演算法分離1。由此，我們可以設計用於不同模型的通用演算法，適用於不同領域。反之， 我們可以改進針對一個特別應用領域的模型，選擇不同的椎理演算法。這使得模型的建立和求解可以分開：根據專業知識來抽象出模型，再基於資料來求解模型引數。

2.1.２ 系統的不確定性 ( Uncertainty )

　　概率圖模型討論涉及不確定性的複雜系統。這是由於比如

• 人們對世界認知的片面性（Partial knowledge of state of the world）
• 觀測資料常帶有“噪聲”（Noisy Observations）
• 我們模型的不全面性（Phenomena not coverd by our model）
• 事件固有的隨機型（Inherent stochasticity）

 　　故課程將涵蓋很多概率論相關知識.

2.1.３ 概率論 ( Probability Theory )

　　Probability Theory 是我們處理不確定性的方法基礎 (theoritical basis of dealing with the uncertainty)，它為我們考慮多個可能的結果及其可能性提供了一種形式框架。

• 對不確定性的表述（Declarative representation with clear semantics）
• 有效力的推理方式（Powerful reasoning patterns）
• 體系化的學習演算法（Established learning methods）

2.2 結構化概率圖模型

2.2.1 複雜系統的聯合分佈

　　概率圖模型是基於複雜系統（complex systems）的建模，它將為題抽象為對一組隨機變數 X1,...,Xn 求聯合分佈 P(X1,...,Xn) 的問題。

2.2.2 有向圖和無向圖

　　概率圖模型分為兩種基本型別：

• 有向圖：貝葉斯網（BNs, Beyas Networks）
• 無向圖：馬爾可夫網（MNs, Markov Networks）

2.2.3 對偶雙重視角

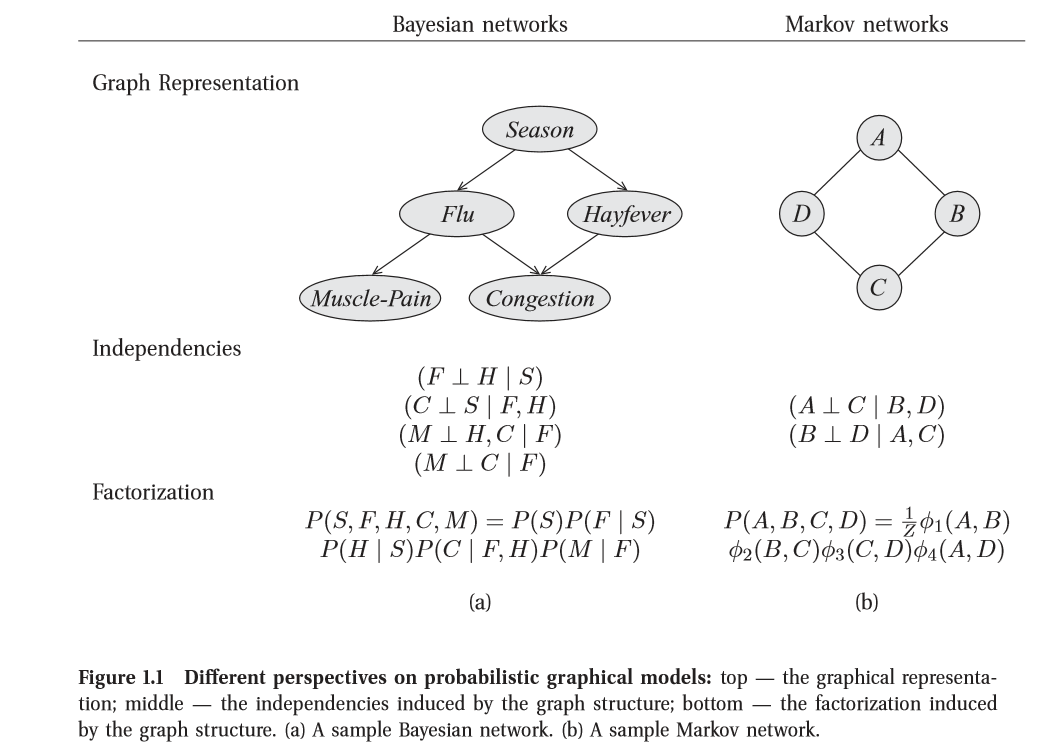
　　概率圖模型把基於圖的表示方法作為高維空間上緊湊編碼複雜分佈的基礎。在下圖中，節點與問題中的變數對應，而邊與兩節點變數之間的直接概率相互對應。
　　對於每個圖模型，無論有向（左圖）或無向（右圖），我們都有對偶雙重視角來說明一個圖的結構。如圖中2的獨立關係（Independence）和因子分解（Factorization）。

• 獨立關係（Independence）

 　　圖是在分佈中蘊含的獨立關係集合的一個緊湊表示：對於一組變數 X,Y,X 而言，這些關係成為“給定 Z 時，變數 X 和 Y 獨立，記作 X⊥Y|Z”;

• 因子分解（Factorization）

 　　圖定義了緊湊表示高緯分佈的一種框架：與其對圖中所有變數可能取值的概率進行編碼， 不如將分佈“分解”為些更小的因子，使每一個因子定義在更小的概率空間上。然後，我們可以將總體的聯合分佈定義為這些因子的乘積。

　　結果是這兩種視角一一圖作為獨立關係集合的表示與圖作為分解分佈的框架一一在深層意義上是等價的。準確地說， 正是分佈的獨立特性才使得分佈能夠緊湊地以因子分解的形式表示。反之，分佈的一個特別的因子分解確保了某些獨立關係的成立。

2.2.4 模型優點

• 將高緯空間的問題用緊湊而有啟發性的結構呈現（Intuitive & compact data structure）；
• 用通用演算法進行高效的推理（Efficient reasoning using general-prupose）；
• 將複雜的問題稀疏引數化（Sparse parameterization）
  
  • 將問題視覺化（feasible eliciation）
  • 從資料中學習（learning from data）

2.2.5 求解過程概述

　　對於概率圖模型的求解要做以下三件事情：

• 1) 表達（Representation）

  • 無向圖和有向圖（direct and undirect）
  • 動態時序（temporal）模型和靜態 plate 模型

• 2) 推斷（Inference）

  • 精確推斷和模糊推斷（尋求計算效率和計算精度的平衡）
  • 在不確定性狀態下進行決策（decision making）

• 3) 學習（Learning）

  • 自動學習引數和結構（parameters and structure）
  • 有完全資料情形和非完全資料情形

2.3 概率圖模型應用

3. Distribution

3.1 貝葉斯法則

　　首先我們需要明確貝葉斯法則（Bayes’ Rule）3。

　　接下來我們將討論三種分佈的概念：聯合分佈、邊緣分佈和條件分佈。

3.2 聯合分佈

　　很多情況下，我們對於幾個變數同時的取值有關問題感興趣，例如我們需要知道事件“ lntellegence = high 且Grade＝ A”的概率。分析這樣的事件，則需要考慮兩個隨機變數的聯合分佈（joint distribution）。下圖為聯合分佈的一個例子。

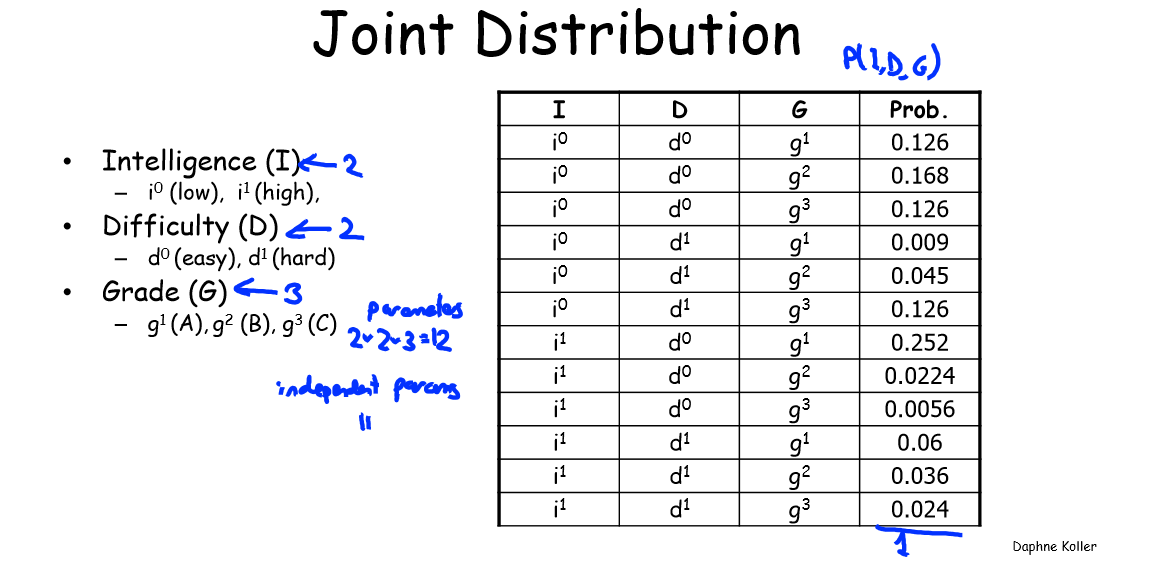
　　上圖表示了隨機變數 I,D,G 的一個聯合分佈，其中包含3個變數，分別是：I（學生智力，有0和1兩個取值）、D（試卷難度，有0和1兩個取值）、G（成績等級，有1、2、3三個取值）。故而這三個離散的隨機變數共有 2×2×3=12 種聯合分佈狀態。
　　上表中我們可以讀出系統取值為這 12 個聯合分佈狀態中任一個的概率，例如：P(I=0,D=0,G=1)=0.126.

3.3 條件分佈

　　 當對於一組隨機變數，考慮其中某些變數取值特定值時，其餘變數的分佈是一種條件分佈問題。可以看到，條件分佈率就是在邊緣分佈率的基礎上都加上“另一個隨機變數取定某值”這個條件。簡單來說，對於二緯離散隨機變數有
　　 P(X=xi|Y=yj)=P(X=xi,Y=yj)P(Y=yj)
　　 為在 Y=yj 條件下 X 的條件分佈率. （其中 i 為固定的），也稱作該聯合分佈在 Y 上的條件分佈。
　　
　　 回到 3.2 中例子來看，下圖中表是概率的聯合分佈，表中隨便去掉所有包含某個值的行，就能對分佈表進行縮減。例如可以去掉所有 G 不為 1 的行，這樣就只剩下了 1、4、7、10 行，這樣他們的概率之和就不為 1 了，所以需要重新標準化（Renormalization），從而推得原聯合分佈在 G 上的條件分佈4。如圖為推導過程。

　　剔除無關取值（G 不為 1 的行）

　　標準化得到的值

　　即得到之前的聯合分佈在變數 Grade（g）上的條件分佈為上圖右邊的表格。
　　
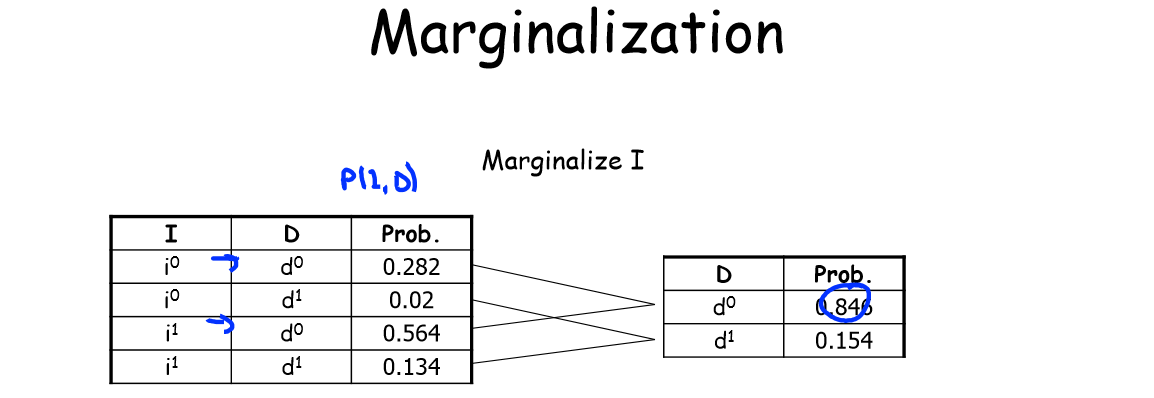
　　反之也可以把所有含有某個值得行相加，這就是接下來要講的邊緣化（Marginalization）。由此可得3.2 中聯合分佈在變數 Ｄ 上的邊緣分佈如下圖右表。

3.4 邊緣分佈

　　一旦定義了隨機變數，我們就可以在能夠用 X 描述的事件上考慮分佈。這個分佈通常稱為隨機變數 X 的邊緣分佈（marginal distribution) ,記為 P(X) . 這時單獨只考慮 X 的取值，與其它隨機變數取什麼值的概率無關了。
　　
　　例如，3.2 中聯合分佈例子裡，I 的邊緣分佈為：
　　P(I=0)=0.126+0.168+0.126+0.009+0.045+0.126.
　　P(I=1)=0.252+0.0224+0.0056+0.06+0.036+0.024.

3.5 一個例子區分三種分佈

　　為了避免混淆三種分佈的定義，這裡舉一個最簡單的例子。設 X,Y 的聯合分佈如下

　　即兩者的邊緣分佈為

　　在 Y=y<