第一題：

煤球數目

有一堆煤球，堆成三角稜錐形。具體：
第一層放1個，
第二層3個（排列成三角形），
第三層6個（排列成三角形），
第四層10個（排列成三角形），
....
如果一共有100層，共有多少個煤球？

請填表示煤球總數目的數字。
注意：你提交的應該是一個整數，不要填寫任何多餘的內容或說明性文字

找規律的題，注意1+2+3+4這樣每層的由來

#include<cstdio>
#include<iostream>
using namespace std;
int main(){
	int a,b;
	int sum=0;
	int num=0;
	for(int i=1;i<=100;i++){
		num=num+i;//1+2+3+4這樣的規律 
		sum=sum+num;
	}
	cout<<sum;
}
 

第二題：


生日蠟燭

某君從某年開始每年都舉辦一次生日party，並且每次都要吹熄與年齡相同根數的蠟燭。

現在算起來，他一共吹熄了236根蠟燭。

請問，他從多少歲開始過生日party的？

請填寫他開始過生日party的年齡數。
注意：你提交的應該是一個整數，不要填寫任何多餘的內容或說明性文字。

直接暴力，先for第一次出生的日子，再for一個結束的日子，最裡面計算開始到結束經歷的總天數

#include<cstdio>
#include<iostream>
using namespace std;
int main(){
	int flag=0;
	for(int i=0;i<236&&(flag==0);i++){
		for(int j=i;j<236&&(flag==0);j++){
			int sum=0;
			for(int k=i;k<=j;k++)
			sum=sum+k;
			if(sum==236)
			cout<<i;
		}
	} 
}
 

湊算式

       B      DEF
A + — + -——— = 10
       C       GHI

（如果顯示有問題，可以參見【圖1.jpg】）

這個算式中A~I代表1~9的數字，不同的字母代表不同的數字。

比如：
6+8/3+952/714 就是一種解法，
5+3/1+972/486 是另一種解法。

這個算式一共有多少種解法？

注意：你提交應該是個整數，不要填寫任何多餘的內容或說明性文字。

next_permutation的應用，如果沒有它，則需要寫一個製造1-9全排列的函式

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
int main(){
	int sum=0;
	double b[10]={1,2,3,4,5,6,7,8,9};
	do{
		if(10==b[0]+b[1]/b[2]+(b[3]*100+b[4]*10+b[5])/(b[6]*100+b[7]*10+b[8]))
		sum++;
	}while(next_permutation(b,b+9));
	cout<<sum;
}
 

第六題：

方格填數

如下的10個格子

（如果顯示有問題，也可以參看【圖1.jpg】）

填入0~9的數字。要求：連續的兩個數字不能相鄰。
（左右、上下、對角都算相鄰）

一共有多少種可能的填數方案？

請填寫表示方案數目的整數。
注意：你提交的應該是一個整數，不要填寫任何多餘的內容或說明性文字。

標記即可，深搜加標記，對每個位置用陣列來表示

#include <stdio.h>
#include<math.h>
#include<iostream>
using namespace std;
int a[11],vis[11];
int count;
void dfs(int x)
{
	if(x>10)//所有方格填數完畢 
	{
		if(abs(a[1]-a[2])>1 && abs(a[1]-a[4])>1 && abs(a[1]-a[5])>1 && abs(a[1]-a[6])>1 &&
		   abs(a[2]-a[3])>1 && abs(a[2]-a[5])>1 && abs(a[2]-a[6])>1 && abs(a[2]-a[7])>1 &&
		   abs(a[3]-a[6])>1 && abs(a[3]-a[7])>1 &&
		   abs(a[4]-a[5])>1 && abs(a[4]-a[8])>1 && abs(a[4]-a[9])>1 &&
		   abs(a[5]-a[6])>1 && abs(a[5]-a[8])>1 && abs(a[5]-a[9])>1 && abs(a[5]-a[10])>1 &&
		   abs(a[6]-a[7])>1 && abs(a[6]-a[9])>1 && abs(a[6]-a[10])>1 &&
		   abs(a[7]-a[10])>1 &&
		   abs(a[8]-a[9])>1 &&
		   abs(a[9]-a[10])>1)
			{
				//輸出每種情況 
//				for(int i=1;i<=10;i++)
//					printf("%d ",a[i]);
//				printf("\n");
				count++;
			}
	}
	for(int i=0;i<=9;i++)
		if(vis[i]==0)
		{
			vis[i]=1;//將用過的數標記 
			a[x]=i;//填數 
			dfs(x+1);//對下一個方格繼續填數 
			vis[i]=0;//清除標記 
		}
}
int main()
{
	count=0;
	dfs(1);
	cout<<count;
	return 0;
}

7.

剪郵票

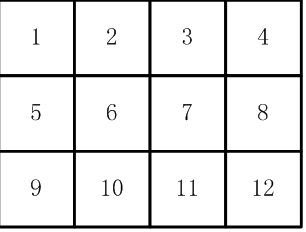
如【圖1.jpg】, 有12張連在一起的12生肖的郵票。

現在你要從中剪下5張來，要求必須是連著的。

（僅僅連線一個角不算相連）

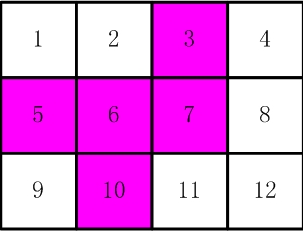
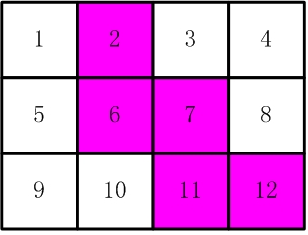
比如，【圖2.jpg】，【圖3.jpg】中，粉紅色所示部分就是合格的剪取。

請你計算，一共有多少種不同的剪取方法。

請填寫表示方案數目的整數。

注意：你提交的應該是一個整數，不要填寫任何多餘的內容或說明性文字。

//列舉5個點，然後dfs判斷聯通性 
#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
int cnt,dir[5]={-4,1,-1,4},a,b,c,d,e,vis[20];
void dfs(int i){
    if(cnt<5)
        for(int j=0;j<4;j++)
        {
            if((i==4||i==8)&&dir[j]==1) continue;//這個一開始忘了 
            if((i==5||i==9)&&dir[j]==-1) continue;
            int t=i+dir[j];
            if(cnt<5&&t>0&&t<13&&!vis[t]&&(t==b||t==c||t==d||t==e))
        {
            vis[t]=1;
            cnt++;
            dfs(t);
        }
        }
}
int main(){
    int ans=0;
    for(a=1;a<=12-4;a++)
    for(b=a+1;b<=12-3;b++)
    for(c=b+1;c<=12-2;c++)
    for(d=c+1;d<=12-1;d++)
    for(e=d+1;e<=12;e++)
    {
        memset(vis,0,sizeof(vis));
        cnt=1;
        dfs(a);
        if(cnt==5) ans++;
    }
    cout<<ans;
}

8.

四平方和

四平方和定理，又稱為拉格朗日定理：

每個正整數都可以表示為至多4個正整數的平方和。

如果把0包括進去，就正好可以表示為4個數的平方和。

比如：

5 = 0^2 + 0^2 + 1^2 + 2^2

7 = 1^2 + 1^2 + 1^2 + 2^2

（^符號表示乘方的意思）

對於一個給定的正整數，可能存在多種平方和的表示法。

要求你對4個數排序：

0 <= a <= b <= c <= d

並對所有的可能表示法按 a,b,c,d 為聯合主鍵升序排列，最後輸出第一個表示法

程式輸入為一個正整數N (N<5000000)

要求輸出4個非負整數，按從小到大排序，中間用空格分開

例如，輸入：

5

則程式應該輸出：

0 0 1 2

再例如，輸入：

12

則程式應該輸出：

0 2 2 2

再例如，輸入：

773535

則程式應該輸出：

1 1 267 838

資源約定：

峰值記憶體消耗 < 256M

CPU消耗  < 3000ms

#include<cstdio>
#include<iostream>
#include<cmath>
using namespace std;
int main(){
	double max,n,d;
	int flag=0;
	cin>>max;
	n=sqrt(max);
	int a,b,c;
	for(a=0;a<n;a++){
		for(b=0;b<n;b++){
			for(c=0;c<n;c++){
				d=sqrt(max-a*a-b*b-c*c);
				if(d==(int)d){//一定這兩個是相等的，取整和未取整的數是相等的
					flag=1;
				}
				if(flag==1)
				break;
			}
			if(flag==1)
			break;
		}
		if(flag==1)
		break;
	}
	cout<<a<<" "<<b<<" "<<c<<" "<<d<<endl;
}

這些就是目前我能解決的題啦，革命尚未成功，同志仍需努力