強連通分支

如果兩個頂點可以相互通達，則稱兩個頂點強連通(strongly connected)。如果有向圖G的每兩個頂點都強連通，稱G是一個強連通圖。非強連通圖有向圖的極大強連通子圖，稱為強連通分量(strongly connected components)。

Tarjan演算法

Tarjan演算法是用來求有向圖的強連通分量的。求有向圖的強連通分量的Tarjan演算法是以其發明者Robert Tarjan命名的。Robert Tarjan還發明瞭求雙連通分量的Tarjan演算法。

流程

對有向圖先任取一個節點，只要這個節點沒被遍歷過，則從其開始進行深度優先遍歷。這裡記錄兩個陣列，dfn[i] and low[i]

還有low[i]，這個就比較難理解了，其實這個記錄的是，當前這個節點i最遠能到之前哪個節點， 例如在圖裡面有一個環：1->2->3->4->1那麼low[4] = dfu[1]，但是假如還包括一條變4->2，那麼指向誰呢？ 答：指向小的那個！ 也就是找最大的強連通分支。

例子

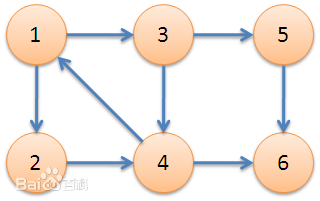
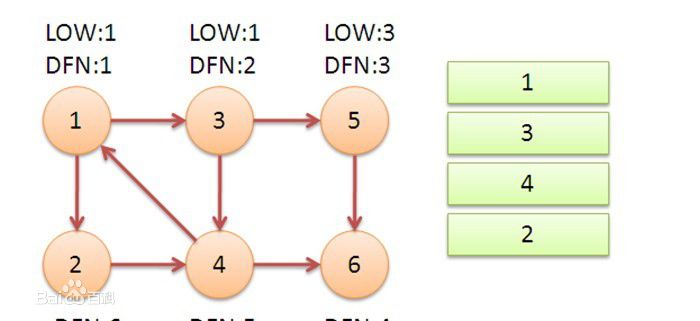
首先我們看這個圖，先用肉眼找一下強連通分支，分別是：{1,2,3,4}, {5}, {6}

那麼對圖開始遍歷，對於深度遍歷，首先從1開始，一直遍歷到6.
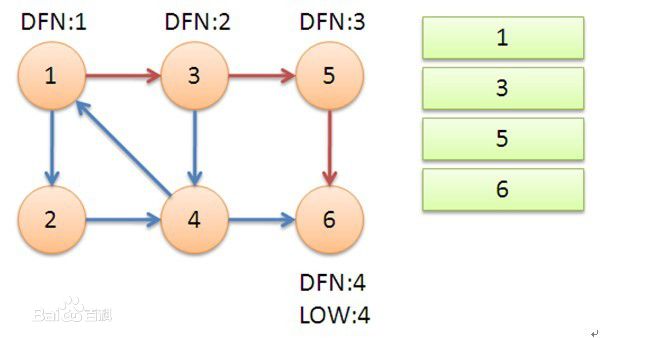
發現6到頭了，然後比較當前節點是不是一個強連通的分支的根( dfu[i] == low[i] 就是)，發現是的，彈棧知道剛好6彈出棧。所彈出棧的所有節點，就是第一個子強連通圖：{6}

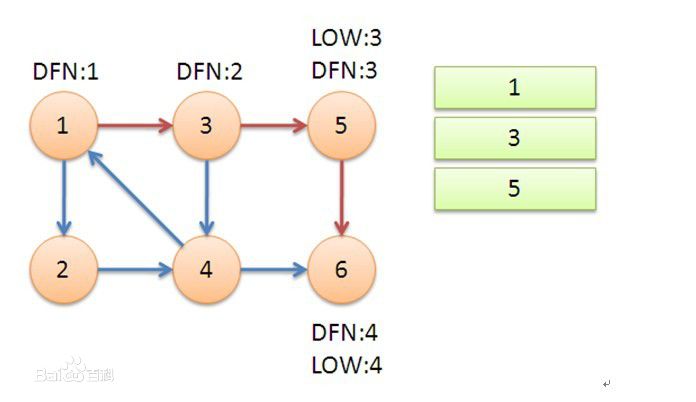
對於5 我們得到low[5] = min(low[5], low[6])，這樣發現，5也是一個根，則彈棧得到：{5}，然後彈棧到3，得到low[3] = min(low[3], low[5]) = 2

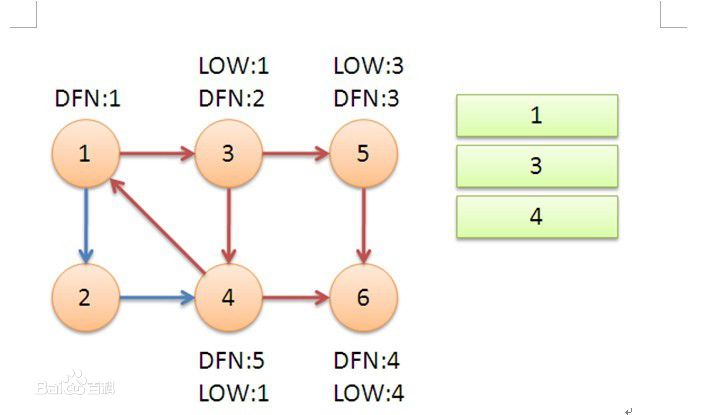
然後3號節點走到4號節點，繼續走到1號節點，發現1號已經在棧裡面了，說明找到一個強連通分支了，那麼讓low[4] = min( low[4], dfn[1] )

再然後遍歷節點2，遍歷到4的時候發現，也已經遍歷過了，但是4在棧裡面，那麼low[2] = min(low[2], dfn[4]) = 5

然後深度遍歷完了，回退到1號節點，發現dfn[1] == low[1]就開始彈棧，得到第三個強連通分支：{1, 2, 3, 4}

程式碼

#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <stack>


using namespace std;

#ifndef MAXNODE
#define MAXNODE 20005
#endif

int flag[MAXNODE] = {0}; //判斷圖中的點是否在棧內
int dfn[MAXNODE] = {0}; //dfu陣列
int low[MAXNODE] = {0}; //low陣列
int tpArr[MAXNODE] = {0}; //存放節點屬於第幾組聯通圖
int tpNum = 0; //對強連通分支設定ID
int _index = 0; //dfs遍歷的ID

vector<int> graph[MAXNODE]; //圖

stack<int> st; //棧

void tarjan(int n){
    st.push(n);
    flag[n] = 1;
    dfn[n] = ++_index;
    low[n] = _index;
    for (int i = 0; i < graph[n].size(); i++) {
        int cur = graph[n][i];
        if (dfn[cur] == 0) {
            tarjan(cur);
            low[n] = min(low[n], low[cur]);
        }else{
            if (flag[cur] == 1) {
                low[n] = min(low[n], dfn[cur]);
            }
        }
    }
    if (dfn[n] == low[n]) {
        tpNum++;
        do{
            n = st.top();
            st.pop();
            flag[n] = 0;
            tpArr[n] = tpNum;
        }while(dfn[n] != low[n]);
    }
}

測試新增圖的程式碼：

int main(){
    int N,T; //節點總數和邊數 節點ID從1開始
    cin>>N>>T;
    int s,e;
    for(int i = 0;i < T; i++){
        cin>>s>>e;
        graph[s].push_back(e);
    }
    for(int i = 1; i <= N; i++){
        if(dfn[i] == 0){
            tarjan(i);
        }
    }
    for(int i = 1; i <= N; i++){
        cout<<tpArr[i]<<' ';
    }
    return 0;
}

自己可以按照上面的圖輸入一下。

這個演算法可以解決2-sat問題