1. 蟻群演算法簡介


     蟻群演算法（Ant Clony Optimization， ACO）是一種群智慧演算法，它是由一群無智慧或有輕微智慧的個體（Agent）通過相互協作而表現出智慧行為，從而為求解複雜問題提供了一個新的可能性。蟻群演算法最早是由義大利學者Colorni A., Dorigo M. 等於1991年提出。經過20多年的發展，蟻群演算法在理論以及應用研究上已經得到巨大的進步。


      蟻群演算法是一種仿生學演算法，是由自然界中螞蟻覓食的行為而啟發的。在自然界中，螞蟻覓食過程中，蟻群總能夠按照尋找到一條從蟻巢和食物源的最優路徑。圖（1）顯示了這樣一個覓食的過程。


image


圖（1）螞蟻覓食


 


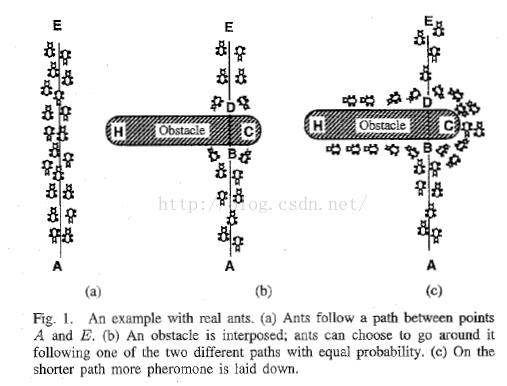
     在圖1（a）中，有一群螞蟻，假如A是蟻巢，E是食物源（反之亦然）。這群螞蟻將沿著蟻巢和食物源之間的直線路徑行駛。假如在A和E之間突然出現了一個障礙物（圖1（b）），那麼，在B點（或D點）的螞蟻將要做出決策，到底是向左行駛還是向右行駛？由於一開始路上沒有前面螞蟻留下的資訊素（pheromone），螞蟻朝著兩個方向行進的概率是相等的。但是當有螞蟻走過時，它將會在它行進的路上釋放出資訊素，並且這種資訊素會議一定的速率散發掉。資訊素是螞蟻之間交流的工具之一。它後面的螞蟻通過路上資訊素的濃度，做出決策，往左還是往右。很明顯，沿著短邊的的路徑上資訊素將會越來越濃（圖1（c）），從而吸引了越來越多的螞蟻沿著這條路徑行駛。


2. TSP問題描述


      蟻群演算法最早用來求解TSP問題，並且表現出了很大的優越性，因為它分散式特性，魯棒性強並且容易與其它演算法結合，但是同時也存在這收斂速度慢，容易陷入區域性最優（local optimal）等缺點。


      TSP問題（Travel Salesperson Problem，即旅行商問題或者稱為中國郵遞員問題），是一種，是一種NP-hard問題，此類問題用一般的演算法是很大得到最優解的，所以一般需要藉助一些啟發式演算法求解，例如遺傳演算法（GA），蟻群演算法（ACO），微粒群演算法（PSO）等等。


      TSP問題可以分為兩類，一類是對稱TSP問題（Symmetric TSP），另一類是非對稱問題（Asymmetric TSP）。所有的TSP問題都可以用一個圖（Graph）來描述：


令


V={c1,c2,…,ci,…,cn},i=1,2,…,nV={c1,c2,…,ci,…,cn},i=1,2,…,n是所有城市的集合. cici表示第i個城市， nn為城市的數目；


E={(r,s):r,s∈V}E={(r,s):r,s∈V}是所有城市之間連線的集合；


C={crs:r,s∈V}C={crs:r,s∈V}是所有城市之間連線的成本度量（一般為城市之間的距離）；


如果crs=csrcrs=csr, 那麼該TSP問題為對稱的，否則為非對稱的。


一個TSP問題可以表達為：


求解遍歷圖G=(V,E,C)G=(V,E,C)，所有的節點一次並且回到起始節點，使得連線這些節點的路徑成本最低。


3. 蟻群演算法原理


      假如蟻群中所有螞蟻的數量為m，所有城市之間的資訊素用矩陣pheromone表示，最短路徑為bestLength，最佳路徑為bestTour。每隻螞蟻都有自己的記憶體，記憶體中用一個禁忌表（Tabu）來儲存該螞蟻已經訪問過的城市，表示其在以後的搜尋中將不能訪問這些城市；還有用另外一個允許訪問的城市表（Allowed）來儲存它還可以訪問的城市；另外還用一個矩陣（Delta）來儲存它在一個迴圈（或者迭代）中給所經過的路徑釋放的資訊素；還有另外一些資料，例如一些控制引數(α，β，ρ，Q)(α，β，ρ，Q)，該螞蟻行走玩全程的總成本或距離（tourLength），等等。假定演算法總共執行MAX_GEN次，執行時間為t。


蟻群演算法計算過程如下：


（1）初始化


設t=0，初始化bestLength為一個非常大的數（正無窮），bestTour為空。初始化所有的螞蟻的Delt矩陣所有元素初始化為0，Tabu表清空，Allowed表中加入所有的城市節點。隨機選擇它們的起始位置（也可以人工指定）。在Tabu中加入起始節點，Allowed中去掉該起始節點。


（2）為每隻螞蟻選擇下一個節點。


為每隻螞蟻選擇下一個節點，該節點只能從Allowed中以某種概率（公式1）搜尋到，每搜到一個，就將該節點加入到Tabu中，並且從Allowed中刪除該節點。該過程重複n-1次，直到所有的城市都遍歷過一次。遍歷完所有節點後，將起始節點加入到Tabu中。此時Tabu表元素數量為n+1（n為城市數量），Allowed元素數量為0。接下來按照（公式2）計算每個螞蟻的Delta矩陣值。最後計算最佳路徑，比較每個螞蟻的路徑成本，然後和bestLength比較，若它的路徑成本比bestLength小，則將該值賦予bestLength，並且將其Tabu賦予BestTour。




（公式1）






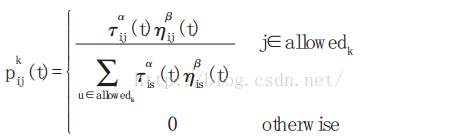
（公式2）


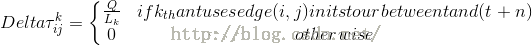
其中p(t)ijpij(t)表示選擇城市j的概率，kk表示第kk個螞蟻，τ(t)ijτij(t)表示城市i,ji,j在第tt時刻的資訊素濃度，ηijηij表示從城市i到城市j的可見度，


ηij=1dijηij=1dij，dijdij表示城市i,ji,j之間的成本（或距離）。由此可見dijdij越小，ηijηij越大，也就是從城市ii到jj的可見性就越大。ΔτkijΔτijk表示螞蟻kk在城市ii與jj之間留下的資訊素。


LkLk表示螞蟻kk經過一個迴圈（或迭代）鎖經過路徑的總成本（或距離），即tourLength.α,β,Qα,β,Q 均為控制引數。


（3）更新資訊素矩陣


令t=t+nt=t+nt，按照（公式3）更新資訊素矩陣phermone。


τij(t+n)=ρ⋅τij(t)+Δτijτij(t+n)=ρ⋅τij(t)+Δτij
（公式3）


τij(t+n)τij(t+n)為t+nt+n時刻城市ii與jj之間的資訊素濃度。ρρ為控制引數，DeltaijDeltaij為城市ii與jj之間資訊素經過一個迭代後的增量。並且有


Δτij=∑k=1mΔτkijΔτij=∑k=1mΔτijk
（公式4）


其中ΔτkijΔτijk由公式計算得到。


（4）檢查終止條件


如果達到最大代數MAX_GEN，演算法終止，轉到第（5）步；否則，重新初始化所有的螞蟻的Delt矩陣所有元素初始化為0，Tabu表清空，Allowed表中加入所有的城市節點。隨機選擇它們的起始位置（也可以人工指定）。在Tabu中加入起始節點，Allowed中去掉該起始節點，重複執行（2），（3）,(4)步。


（5）輸出最優值


4. Java實現


      在該java實現中我們選擇使用tsplib上的資料att48，這是一個對稱tsp問題，城市規模為48，其最優值為10628.其距離計算方法如圖（2）所示：




圖（2）att48距離計算方法


      實現中，使用了兩個java類，一個Ant類，一個ACO類。


具體實現程式碼如下（此程式碼借鑑了蟻群優化演算法的JAVA實現）：


Ant類：


  1: import java.util.Random;
  2: import java.util.Vector;
  3: 
  4: /**
  5:  * 
  6:  * @author BIAO YU
  7:  *
  8:  */
  9: public class Ant implements Cloneable {
 10: 
 11:   private Vector<Integer> tabu; //禁忌表
 12:   private Vector<Integer> allowedCities; //允許搜尋的城市
 13:   private float[][] delta; //資訊數變化矩陣
 14:   private int[][] distance; //距離矩陣
 15:   
 16:   private float alpha; 
 17:   private float beta;
 18:   
 19:   private int tourLength; //路徑長度
 20:   private int cityNum; //城市數量
 21:   
 22:   private int firstCity; //起始城市
 23:   private int currentCity; //當前城市
 24:   
 25:   public Ant(){
 26:     cityNum = 30;
 27:     tourLength = 0;
 28:     
 29:   }
 30:   
 31:   /**
 32:    * Constructor of Ant
 33:    * @param num 螞蟻數量
 34:    */
 35:   public Ant(int num){
 36:     cityNum = num;
 37:     tourLength = 0;
 38:     
 39:   }
 40:   
 41:   /**
 42:    * 初始化螞蟻，隨機選擇起始位置
 43:    * @param distance 距離矩陣
 44:    * @param a alpha
 45:    * @param b beta
 46:    */
 47:   public void init(int[][] distance, float a, float b){
 48:     alpha = a;
 49:     beta = b;
 50:     allowedCities = new Vector<Integer>();
 51:     tabu = new Vector<Integer>();
 52:     this.distance = distance;
 53:     delta = new float[cityNum][cityNum];
 54:     for (int i = 0; i < cityNum; i++) {
 55:       Integer integer = new Integer(i);
 56:       allowedCities.add(integer);
 57:       for (int j = 0; j < cityNum; j++) {
 58:         delta[i][j] = 0.f;
 59:       }
 60:     }
 61:     
 62:     Random random = new Random(System.currentTimeMillis());
 63:     firstCity = random.nextInt(cityNum);
 64:     for (Integer i:allowedCities) {
 65:       if (i.intValue() == firstCity) {
 66:         allowedCities.remove(i);
 67:         break;
 68:       }
 69:     }
 70:     
 71:     tabu.add(Integer.valueOf(firstCity));
 72:     currentCity = firstCity;
 73:   }
 74:   
 75:   /**
 76:    * 選擇下一個城市
 77:    * @param pheromone 資訊素矩陣
 78:    */
 79:   public void selectNextCity(float[][] pheromone){
 80:     float[] p = new float[cityNum];
 81:     float sum = 0.0f;
 82:     //計算分母部分
 83:     for (Integer i:allowedCities) {
 84:       sum += Math.pow(pheromone[currentCity][i.intValue()], alpha)*Math.pow(1.0/distance[currentCity][i.intValue()], beta);
 85:     }
 86:     //計算概率矩陣
 87:     for (int i = 0; i < cityNum; i++) {
 88:       boolean flag = false;
 89:       for (Integer j:allowedCities) {
 90:         
 91:         if (i == j.intValue()) {
 92:           p[i] = (float) (Math.pow(pheromone[currentCity][i], alpha)*Math.pow(1.0/distance[currentCity][i], beta))/sum;
 93:           flag = true;
 94:           break;
 95:         }
 96:       }
 97:       
 98:       if (flag == false) {
 99:         p[i] = 0.f;
100:       }
101:     }
102:     
103:     //輪盤賭選擇下一個城市
104:     Random random = new Random(System.currentTimeMillis());
105:     float sleectP = random.nextFloat();
106:     int selectCity = 0;
107:     float sum1 = 0.f;
108:     for (int i = 0; i < cityNum; i++) {
109:       sum1 += p[i];
110:       if (sum1 >= sleectP) {
111:         selectCity = i;
112:         break;
113:       }
114:     }
115:     
116:     //從允許選擇的城市中去除select city
117:     for (Integer i:allowedCities) {
118:       if (i.intValue() == selectCity) {
119:         allowedCities.remove(i);
120:         break;
121:       }
122:     }
123:     //在禁忌表中新增select city
124:     tabu.add(Integer.valueOf(selectCity));
125:     //將當前城市改為選擇的城市
126:     currentCity = selectCity;
127:     
128:   }
129:   
130:   /**
131:    * 計算路徑長度
132:    * @return 路徑長度
133:    */
134:   private int calculateTourLength(){
135:     int len = 0;
136:     for (int i = 0; i < cityNum; i++) {
137:       len += distance[this.tabu.get(i).intValue()][this.tabu.get(i+1).intValue()];
138:     }
139:     return len;
140:   }
141:   
142:   
143:   
144:   public Vector<Integer> getAllowedCities() {
145:     return allowedCities;
146:   }
147: 
148:   public void setAllowedCities(Vector<Integer> allowedCities) {
149:     this.allowedCities = allowedCities;
150:   }
151: 
152:   public int getTourLength() {
153:     tourLength = calculateTourLength();
154:     return tourLength;
155:   }
156:   public void setTourLength(int tourLength) {
157:     this.tourLength = tourLength;
158:   }
159:   public int getCityNum() {
160:     return cityNum;
161:   }
162:   public void setCityNum(int cityNum) {
163:     this.cityNum = cityNum;
164:   }
165: 
166:   public Vector<Integer> getTabu() {
167:     return tabu;
168:   }
169: 
170:   public void setTabu(Vector<Integer> tabu) {
171:     this.tabu = tabu;
172:   }
173: 
174:   public float[][] getDelta() {
175:     return delta;
176:   }
177: 
178:   public void setDelta(float[][] delta) {
179:     this.delta = delta;
180:   }
181: 
182:   public int getFirstCity() {
183:     return firstCity;
184:   }
185: 
186:   public void setFirstCity(int firstCity) {
187:     this.firstCity = firstCity;
188:   }
189:   
190: }
191: 
ACO類：


  1: import java.io.BufferedReader;
  2: import java.io.FileInputStream;
  3: import java.io.IOException;
  4: import java.io.InputStreamReader;
  5: 
  6: /**
  7:  * 
  8:  * @author BIAO YU
  9:  * 
 10:  *
 11:  */
 12: public class ACO {
 13: 
 14:   private Ant[] ants; //螞蟻
 15:   private int antNum; //螞蟻數量
 16:   private int cityNum; //城市數量
 17:   private int MAX_GEN; //執行代數
 18:   private float[][] pheromone; //資訊素矩陣
 19:   private int[][] distance; //距離矩陣
 20:   private int bestLength; //最佳長度
 21:   private int[] bestTour; //最佳路徑
 22:   
 23:   //三個引數
 24:   private float alpha; 
 25:   private float beta;
 26:   private float rho;
 27:   
 28:   
 29:   public ACO(){
 30:     
 31:   }
 32:   /** constructor of ACO
 33:    * @param n 城市數量
 34:    * @param m 螞蟻數量
 35:    * @param g 執行代數
 36:    * @param a alpha
 37:    * @param b beta
 38:    * @param r rho
 39:    * 
 40:   **/
 41:   public ACO(int n, int m, int g, float a, float b, float r) {
 42:     cityNum = n;
 43:     antNum = m;
 44:     ants = new Ant[antNum];
 45:     MAX_GEN = g;
 46:     alpha = a;
 47:     beta = b;
 48:     rho = r;
 49:     
 50:   }
 51:   
 52:   @SuppressWarnings("resource")
 53:   /**
 54:    * 初始化ACO演算法類
 55:    * @param filename 資料檔名，該檔案儲存所有城市節點座標資料
 56:    * @throws IOException
 57:    */
 58:   private void init(String filename) throws IOException{
 59:     //讀取資料  
 60:         int[] x;  
 61:         int[] y;  
 62:         String strbuff;  
 63:         BufferedReader data = new BufferedReader(new InputStreamReader(new FileInputStream(filename)));  
 64:         
 65:         distance = new int[cityNum][cityNum];  
 66:         x = new int[cityNum];  
 67:         y = new int[cityNum];  
 68:         for (int i = 0; i < cityNum; i++) {  
 69:             strbuff = data.readLine(); 
 70:             String[] strcol = strbuff.split("");  
 71:             x[i] = Integer.valueOf(strcol[1]);  
 72:             y[i] = Integer.valueOf(strcol[2]);  
 73:         }  
 74:         //計算距離矩陣 ，針對具體問題，距離計算方法也不一樣，此處用的是att48作為案例，它有48個城市，距離計算方法為偽歐氏距離，最優值為10628 
 75:         for (int i = 0; i < cityNum - 1; i++) {  
 76:             distance[i][i] = 0;  //對角線為0
 77:             for (int j = i + 1; j < cityNum; j++) {  
 78:               double rij = Math.sqrt(((x[i] - x[j]) * (x[i] - x[j])+ (y[i] - y[j]) * (y[i] - y[j]))/10.0);
 79:               int tij = (int) Math.round(rij);
 80:               if (tij < rij) {
 81:                 distance[i][j] = tij + 1;  
 82:                     distance[j][i] = distance[i][j];  
 83:         }else {
 84:           distance[i][j] = tij;  
 85:                     distance[j][i] = distance[i][j]; 
 86:         }
 87:             }  
 88:         }  
 89:         distance[cityNum - 1][cityNum - 1] = 0;  
 90:         
 91:         //初始化資訊素矩陣  
 92:         pheromone=new float[cityNum][cityNum];  
 93:         for(int i=0;i<cityNum;i++)  
 94:         {  
 95:             for(int j=0;j<cityNum;j++){  
 96:                 pheromone[i][j]=0.1f;  //初始化為0.1
 97:             }  
 98:         }  
 99:         bestLength=Integer.MAX_VALUE;  
100:         bestTour=new int[cityNum+1];  
101:         //隨機放置螞蟻  
102:         for(int i=0;i<antNum;i++){  
103:             ants[i]=new Ant(cityNum);  
104:             ants[i].init(distance, alpha, beta);  
105:         }  
106:   }
107:   
108:   public void solve(){
109:     
110:     for (int g = 0; g < MAX_GEN; g++) {
111:       for (int i = 0; i < antNum; i++) {
112:         for (int j = 1; j < cityNum; j++) {
113:           ants[i].selectNextCity(pheromone);
114:         }
115:         ants[i].getTabu().add(ants[i].getFirstCity());
116:         if (ants[i].getTourLength() < bestLength) {
117:           bestLength = ants[i].getTourLength();
118:           for (int k = 0; k < cityNum + 1; k++) {
119:             bestTour[k] = ants[i].getTabu().get(k).intValue();
120:           }
121:         }
122:         for (int j = 0; j < cityNum; j++) {
123:           ants[i].getDelta()[ants[i].getTabu().get(j).intValue()][ants[i].getTabu().get(j+1).intValue()] = (float) (1./ants[i].getTourLength());
124:           ants[i].getDelta()[ants[i].getTabu().get(j+1).intValue()][ants[i].getTabu().get(j).intValue()] = (float) (1./ants[i].getTourLength());
125:         }
126:       }
127:       
128:       //更新資訊素
129:       updatePheromone();
130:       
131:        //重新初始化螞蟻
132:           for(int i=0;i<antNum;i++){  
133:              
134:               ants[i].init(distance, alpha, beta);  
135:           }  
136:     }
137:     
138:     //列印最佳結果
139:     printOptimal();
140:   }
141:   
142:   //更新資訊素
143:   private void updatePheromone(){
144:     //資訊素揮發  
145:         for(int i=0;i<cityNum;i++)  
146:             for(int j=0;j<cityNum;j++)  
147:                 pheromone[i][j]=pheromone[i][j]*(1-rho);  
148:         //資訊素更新  
149:         for(int i=0;i<cityNum;i++){  
150:             for(int j=0;j<cityNum;j++){  
151:                 for (int k = 0; k < antNum; k++) {
152:           pheromone[i][j] += ants[k].getDelta()[i][j];
153:         } 
154:             }  
155:         }  
156:   }
157:   
158:   private void printOptimal(){
159:     System.out.println("The optimal length is: " + bestLength);
160:     System.out.println("The optimal tour is: ");
161:     for (int i = 0; i < cityNum + 1; i++) {
162:       System.out.println(bestTour[i]);
163:     }
164:   }
165:   
166:   public Ant[] getAnts() {
167:     return ants;
168:   }
169: 
170:   public void setAnts(Ant[] ants) {
171:     this.ants = ants;
172:   }
173: 
174:   public int getAntNum() {
175:     return antNum;
176:   }
177: 
178:   public void setAntNum(int m) {
179:     this.antNum = m;
180:   }
181: 
182:   public int getCityNum() {
183:     return cityNum;
184:   }
185: 
186:   public void setCityNum(int cityNum) {
187:     this.cityNum = cityNum;
188:   }
189: 
190:   public int getMAX_GEN() {
191:     return MAX_GEN;
192:   }
193: 
194:   public void setMAX_GEN(int mAX_GEN) {
195:     MAX_GEN = mAX_GEN;
196:   }
197: 
198:   public float[][] getPheromone() {
199:     return pheromone;
200:   }
201: 
202:   public void setPheromone(float[][] pheromone) {
203:     this.pheromone = pheromone;
204:   }
205: 
206:   public int[][] getDistance() {
207:     return distance;
208:   }
209: 
210:   public void setDistance(int[][] distance) {
211:     this.distance = distance;
212:   }
213: 
214:   public int getBestLength() {
215:     return bestLength;
216:   }
217: 
218:   public void setBestLength(int bestLength) {
219:     this.bestLength = bestLength;
220:   }
221: 
222:   public int[] getBestTour() {
223:     return bestTour;
224:   }
225: 
226:   public void setBestTour(int[] bestTour) {
227:     this.bestTour = bestTour;
228:   }
229: 
230:   public float getAlpha() {
231:     return alpha;
232:   }
233: 
234:   public void setAlpha(float alpha) {
235:     this.alpha = alpha;
236:   }
237: 
238:   public float getBeta() {
239:     return beta;
240:   }
241: 
242:   public void setBeta(float beta) {
243:     this.beta = beta;
244:   }
245: 
246:   public float getRho() {
247:     return rho;
248:   }
249: 
250:   public void setRho(float rho) {
251:     this.rho = rho;
252:   }
253: 
254: 
255:   /**
256:    * @param args
257:    * @throws IOException 
258:    */
259:   public static void main(String[] args) throws IOException {
260:     ACO aco = new ACO(48, 100, 1000, 1.f, 5.f, 0.5f);
261:     aco.init("c://data.txt");
262:     aco.solve();
263:   }
264: 
265: }
266: 
5. 總結


      蟻群演算法和其它的啟發式演算法一樣，在很多場合都得到了應用，並且取得了很好的結果。但是同樣存在著很多的缺點，例如收斂速度慢，容易陷入區域性最優，等等。對於這些問題，還需要進一步的研究和探索，另外蟻群演算法的數學機理至今還沒有得到科學的解釋，這也是當前研究的熱點和急需解決的問題之一。注：TSP資料檔案以及兩篇早期的關於蟻群演算法的文章包含在附件中，請點選此處