資料結構----完全二叉樹和滿二叉樹以及前序、中序、後序遍歷
一) 滿二叉樹和完全二叉樹
1.滿二叉樹定義:
又叫Full Binary Tree. 除最後一層無任何子節點外,每一層上的所有結點都有兩個子結點(最後一層上的無子結點的結點為葉子結點)。也可以這樣理解,除葉子結點外的所有結點均有兩個子結點。節點數達到最大值。所有葉子結點必須在同一層上。
如圖:
2.完全二叉樹定義:
完全二叉樹(Complete Binary Tree)
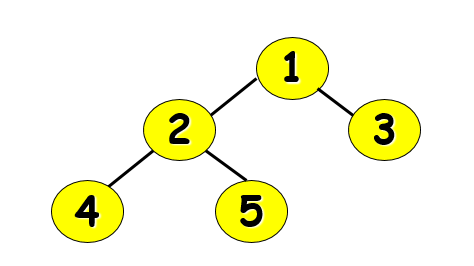
若設二叉樹的深度為h,除第 h 層外,其它各層 (1~h-1) 的結點數都達到最大個數,第 h 層所有的結點都連續集中在最左邊,這就是完全二叉樹。
這裡可以看到第2層所有的節點都集中在了最左邊!!!!!!
完全二叉樹是由滿二叉樹而引出來的。對於深度為K的,有n個結點的二叉樹,當且僅當其每一個結點都與深度為K的滿二叉樹中編號從1至n的結點一一對應時稱之為完全二叉樹。
注意:
一棵二叉樹至多隻有最下面的一層上的結點的度數可以小於2,並且最下層上的結點都集中在該層最左邊的若干位置上,則此二叉樹成為完全二叉樹。
二)前序、中序、後序遍歷
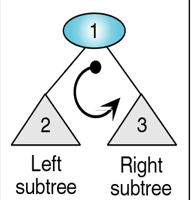
前序遍歷:
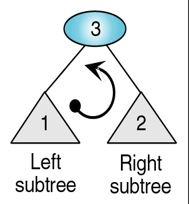
遍歷的順序是:根節點-左節點-右節點
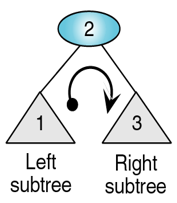
中序遍歷:
遍歷的順序是:左節點-根節點-右節點
後序遍歷:
遍歷的順序是:左節點-右節點-根節點
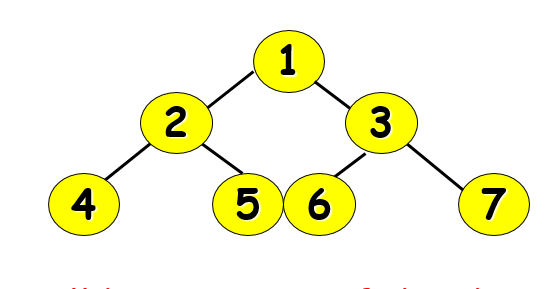
例子:
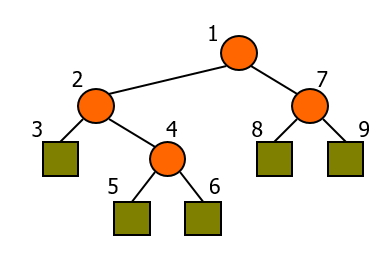
前序遍歷法:123456789(根左右)
中序遍歷法:325461879(左根右)
後序遍歷法:356428971(左右根)
補充兩個例子:
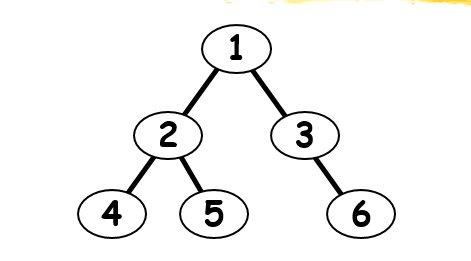
前序124536 (根左右)
中序425136(左根右)
後序452631(左右根)
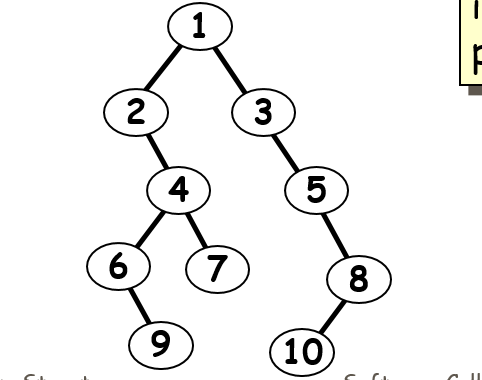
前序12469735810(根左右)
中序26947135108(左根右)
後序96742108531(左右根)
相關推薦
資料結構----完全二叉樹和滿二叉樹以及前序、中序、後序遍歷
一) 滿二叉樹和完全二叉樹 1.滿二叉樹定義: 又叫Full Binary Tree. 除最後一層無任何子節點外,每一層上的所有結點都有兩個子結點(最後一層上的無子結點的結點為葉子結點)。也可以這樣理解,除葉子結點外的所有結點均有兩個子結點。節點數達到最大值
完全二叉樹和滿二叉樹的區別+完全二叉樹求節點問題
今天覆習了下二叉樹的相關知識,發現很多都忘掉了,所以在此記錄下 滿二叉樹 如圖,顧名思義,滿二叉樹說白了其實就是除了最後一層,所有節點都有兩個孩子, 所以: 假設現在有一棵深度為N的滿二叉樹: 總結點數就是2^N-1(計算公式:
完全二叉樹和滿二叉樹的區別
堆的話一般都是用完全二叉樹來實現的,比如大堆和小堆。一個樹節點的度數就是這個樹節點有多少子節點,和樹的深度意義不同。 依據二叉樹的性質,完全二叉樹和滿二叉樹採用順序儲存比較合適 完全二叉樹是效率很高的資料結構,堆是一種完全二叉樹或者近似完全二叉樹,所以效率極高,像
判斷完全二叉樹和滿二叉樹
(一)判斷完全二叉樹 特點一: 只允許最後一層有空缺結點且空缺在右邊,即葉子結點只能在層次最大的兩層上出現; 特點二: 對任一結點,如果其右子樹的深度為j,則其左子樹的深度必為j或j+1 即度為1的點只有1個或0個 解題思路: 首先一棵空樹是完全二叉樹 利用佇
【資料結構】C語言最基礎練習:棧的初始化,壓棧,出棧,遍歷,清空
隨手練習一下,詳細程式碼解釋都在程式碼片裡請仔細看看 如果有什麼不對的地方,請在下方留言 先建立標頭檔案: #define _CRT_SECURE_NO_WARNINGS 1 #ifndef _TEST_H #define _TEST_H //棧的鏈式儲存結構;
二叉樹基本概念(滿二叉樹、完全二叉樹,滿二叉樹,二叉樹的遍歷)
1. 二叉樹 二叉樹是每個節點最多有兩個子樹的樹結構。它有五種基本形態:二叉樹可以是空集;根可以有空的左子樹或右子樹;或者左、右子樹皆為空。 性質1:二叉樹第i層上的結點數目最多為 2{i-1} (i≥1)。性質2:深度為k的二叉樹至多有2{k}-1個結點(k≥1)
【圖解資料結構】 一組動畫徹底理解二叉樹三種遍歷
二叉樹的遍歷是指從根結點出發,按照某種次序依次訪問二叉樹中所有結點,使得每個結點被訪問一次且僅被訪問一次。 在二叉樹的遍歷中存在三種較為常用的遍歷方式:前序遍歷、中序遍歷、後序遍歷。接下來我將嘗試著用三組動畫向讀者詳細的介紹這三種遍歷方式的邏輯思路,希望讓讀者看到任何的二叉樹都能在腦海中快速的勾勒出動畫。
[PTA] 資料結構與演算法題目集 6-12 二叉搜尋樹的操作集
唯一比較需要思考的刪除操作: 被刪除節點有三種情況: 1、葉節點,直接刪除 2、只有一個子節點,將子節點替換為該節點,刪除該節點。 3、有兩個子節點,從右分支中找到最小節點,將其值賦給被刪除節點的位置,接著刪除這個最小節點 // 函式Insert將X插入二叉搜尋樹BST並返
資料結構的Java實現(十)—— 二叉樹
目錄 樹 二叉樹 樹 樹(tree)是一種抽象資料型別(ADT),用來模擬具有樹狀結構性質的資料集合。它是由n(n>=0)個有限節點組成一個具有層次關係的集合。節點一般代表一些實體,在java中節點一般代表物件。連線節點的線稱為邊,一般從一個節點到另一個節點的唯
完全二叉樹,滿二叉樹,霍夫曼樹
霍夫曼樹:每個節點要嘛沒有子節點,要麼有兩個子節點 完全二叉樹:滿二叉樹的一部分或者全部。 滿二叉樹:每個父親都有2個葉子。 1 1 / \
基礎資料結構與演算法實現(2)—二叉搜尋樹BST
import java.util.LinkedList; import java.util.Queue; public class BST <E extends Comparable<E>> { private c
二叉樹,完全二叉樹,滿二叉樹,二叉排序樹,平衡二叉樹,紅黑樹,B數,B-樹,B+樹,B*樹(一)
二叉樹 二叉樹:二叉樹是每個節點最多有兩個子樹的樹結構; 是n(n>=0)個結點的有限集合,它或者是空樹(n=0),或者是由一個根結點及兩顆互不相交的、分別稱為左子樹和右子樹的二叉樹所組成。 完全二叉樹 完全二叉樹:除最後一層外,每一層上的結點數均達到最
二叉樹,完全二叉樹,滿二叉樹,二叉排序樹,平衡二叉樹,紅黑樹,B數,B-樹,B+樹,B*樹(二)
二叉樹,完全二叉樹,滿二叉樹,二叉排序樹,平衡二叉樹,紅黑樹,B數,B-樹,B+樹,B*樹(一): BST樹 即二叉搜尋樹: 1.所有非葉子結點至多擁有兩個兒子(Left和Right); 2.所有結點儲存一個關鍵字;
完美二叉樹, 完全二叉樹和完滿二叉樹
樹在資料結構中佔有非常重要的地位。本文從樹的基本概念入手,給出完美(Perfect)二叉樹,完全(Complete)二叉樹和完滿(Full)二叉樹的區別。如果學習過二叉樹,但是對這三種二叉樹並沒有深入的理解,或者完全被國產資料結構教科書所誤導(只聽說過滿二叉樹和完全二叉樹)的朋友不妨花點時間耐著性子將本文仔細
資料結構與演算法(C語言) | 二叉排序樹
二叉排序樹的定義—— 二叉排序樹 ( Binary Sort Tree) 或者為空;或者是具有如下特性的二叉樹: (1)若根的左子樹不空,則左子樹上所有結點的關鍵字均小於根結點的關鍵字; (2)若
完全二叉樹與滿二叉樹
去筆試了很多次,每次都有有關於二叉樹的題目,而且其中最多的是關於完全二叉樹,然而完全二叉樹在哥心中的形態一直很模糊,究其原因是我把完全二叉樹和滿二叉樹搞混了。其實滿二叉樹是完全二叉樹的特例,因為滿二叉樹已經滿了,而完全並不代表滿。所以形態你也應該想象出來了吧,滿指的是出了葉
二叉樹,完全二叉樹,滿二叉樹,平衡二叉樹的區別
度:指的是一個節點擁有子節點的個數。如二叉樹的節點的最大度為2。 深度:數的層數,根節點為第一層,依次類推。 葉子節點:度為0的節點,即沒有子節點的節點。 樹:樹中的每一個節點,可以有n(後續節點)個子節點,但是每個節點只有一個前驅節點。 二叉樹:除了葉子節點外,每個節點
完全二叉樹與滿二叉樹與霍夫曼樹
去筆試了很多次,每次都有有關於二叉樹的題目,而且其中最多的是關於完全二叉樹,然而完全二叉樹在哥心中的形態一直很模糊,究其原因是我把完全二叉樹和滿二叉樹搞混了。其實滿二叉樹是完全二叉樹的特例,因為滿二叉樹已經滿了,而完全並不代表滿。所以形態你也應該想象出來了吧,滿指的是出了
【資料結構】資料結構C語言的實現(簡單二叉樹)
簡單二叉樹 /* * 二叉樹 */ #include <stdio.h> #include <stdlib.h> #define TRUE 1 #define FAL
數據結構 第5章 樹的二叉樹 單元小結(2)遍歷二叉樹和線索二叉樹
進行 深度 bsp iteration oid 基礎 二叉樹 線索 push 概念: 遍歷二叉樹: 遍歷:指按某條搜索路線遍訪每個結點且不重復(又稱周遊)。 遍歷的用途:它是樹結構插入、刪除、修改、查找和排序運算的前提,是二叉樹一切運算的基礎和核心。 時間效率: O