2. 程式人生 > >LDA主題模型三連擊-入門/理論/程式碼

LDA主題模型三連擊-入門/理論/程式碼

阿新 • • 發佈：2019-01-19

本文將從三個方面介紹LDA主題模型——整體概況、數學推導、動手實現。
關於LDA的文章網上已經有很多了，大多都是從經典的《LDA 數學八卦》中引出來的，原創性不太多。
本文將用盡量少的公式，跳過不需要的證明，將最核心需要學習的部分與大家分享，展示出直觀的理解和基本的數學思想，避免數學八卦中過於詳細的推導。最後用python 進行實現。

概況

第一部分，包括以下四部分。

  • 為什麼需要
  • LDA是什麼
  • LDA的應用
  • LDA的使用

為什麼需要

挖掘隱含語義資訊。一個經典的例子是

“喬布斯離我們而去了。”
“蘋果價格會不會降？”

上面這兩個句子沒有共同出現的單詞，但這兩個句子是相似的，如果按傳統的方法判斷這兩個句子肯定不相似。
所以在判斷文件相關性的時候需要考慮到文件的語義，而語義挖掘的利器是主題模型，LDA就是其中一種比較有效的模型。

LDA是什麼

LDA主題模型，首先是在文字分類領域提出來的，它的本意是挖掘文字中的隱藏主題。它將文字看作是詞袋模型(文章中的詞之間沒有關聯)產生的過程看成 先選一堆主題，再在主題中選擇詞，以此構建了一篇文章。
d是文章
z1...zn是主題
w 是單詞
θmk是文件選擇主題的概率。
φkt是主題選擇詞的概率。
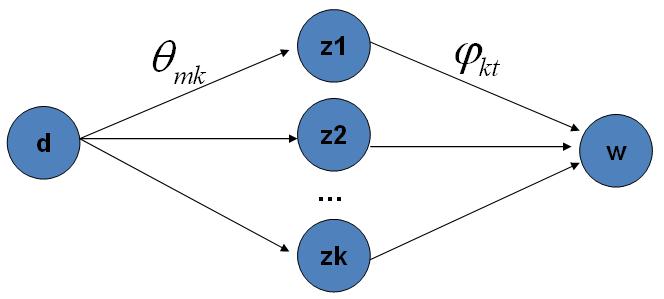
這裡寫圖片描述
這裡新手比較困惑的一點是選來選取，變數是什麼？
你可以這樣理解，先不要管狄利克雷分佈，明確是從topic分佈上選取topic，得到各topic的概率，然後再去另一個詞的分佈上選取剛才得到topic對應的詞。

這裡寫圖片描述

這裡寫圖片描述
注意：此時不用想這兩個分佈怎麼來的，只要把這個過程能想明白即可。LDA產生文件的過程。
選主題分佈->選主題

Created with Raphaël 2.1.0設定狄利克雷分佈引數α設定狄利克雷分佈引數α生成主題分佈生成主題分佈設定狄利克雷分佈引數β設定狄利克雷分佈引數β生成主題的詞分佈生成主題的詞分佈選取主題t選取主題t生成主題t的詞分佈生成主題t的詞分佈生成詞生成詞

LDA的應用

通過隱含語義找到關聯項。
相似文件發現；
推薦商品；將該商品歸屬的主題下其他商品推薦給使用者
主題評分；分析文件主題傾向，看哪個主題比重大

gensim應用

import jieba
import gensim
def load_stop_words(file_path):
    stop_words = []
    with
 
 open(file_path,encoding='utf8') as f:
        for word in f:
            stop_words.append(word.strip())
    return stop_words
def pre_process(data):
    # jieba 分詞
    cut_list = list(map(lambda x: '/'.join(jieba.cut(x,cut_all=True)).split('/'), data))
    # 載入停用詞 去除 "的 了 啊 "等
    stop_words = load_stop_words('stop_words.txt')
    final_word_list = []
    for cut in cut_list:
        # 去除掉空字元和停用詞
        final_word_list.append(list(filter(lambda x: x != '' and x not in stop_words, cut)))
    print(final_word_list)
    word_count_dict = gensim.corpora.Dictionary(final_word_list)
    # 轉成詞袋模型 每篇文章由詞字典中的序號構成
    bag_of_words_corpus = [word_count_dict.doc2bow(pdoc) for pdoc in final_word_list]
    print(bag_of_words_corpus)
    #返回 詞袋庫 詞典
    return bag_of_words_corpus, word_count_dict

def train_lda(bag_of_words_corpus, word_count_dict):
    # 生成lda model
    lda_model = gensim.models.LdaModel(bag_of_words_corpus, num_topics=10, id2word=word_count_dict)
    return lda_model

# 新聞地址 http://news.xinhuanet.com/world/2017-12/08/c_1122082791.htm

train_data = [u"中方對我們的建交國同臺灣開展正常經貿和民間往來不持異議，但堅決反對我們的建交國同臺灣發生任何形式的官方往來或簽署任何帶有主權意涵的協定或合作檔案",
     u"灣與菲律賓簽署了投資保障協定等７項合作檔案。菲律賓是臺灣推動“新南向”政策中首個和臺灣簽署投資保障協定的國家。",
     u"中方堅決反對建交國同臺灣發生任何形式的官方往來或簽署任何帶有主權意涵的協定或合作檔案，已就此向菲方提出交涉"]
processed_train_data = pre_process(train_data)

lda_model = train_lda(*processed_train_data)
lda_model.print_topics(10)

數學原理

通過上節內容，在工程上基本可以用起來了。但是大家都是有追求的，不僅滿足使用。這節簡單介紹背後的數學原理。只會將核心部分的數學知識拿出來，不會面面俱到（我覺得這部分理解就足夠了）
（詳盡內容推薦去看《數學八卦》）

LDA認為各個主題的概率和各個主題下單詞的概率不是固定不變的（比如通過設定3個主題的抽取概率為0.3 0.4 0.3 就一直這麼用），而是由先驗和樣本共同通過貝葉斯計算得到的一個分佈，同時還會依據不斷新增加的樣本進行調整。pLSA（LDA的前身） 看待分佈情況就是固定的，求完就求完了，而LDA看待分佈情況是 不斷依據先驗和樣本調整。

預備知識

下面我們來介紹一下貝葉斯公式
P(θ|X)=P(X|θ)P(θ)P(X)
其中
後驗概率 P(θ|X) 就是說在觀察到X個樣本情況下,θ的概率
先驗概率 P(θ) 人們歷史經驗，比如硬幣正反概率0.5 骰子每個面是1/6
似然函式 P(X|θ) 在θ下，觀察到X個樣本的概率

貝葉斯估計簡單來說
先驗分佈 + 資料的知識 = 後驗分佈（嚴格的數學推導請看數學八卦）

Beta(p|α,β)+Count(m1,m2)=Beta(p|α+m1,β+m2)

對於選主題，選單詞這個過程，LDA將其主題，單詞的分佈看作是兩個後驗概率來求解。因為這兩個過程每次的結果都和骰子類似，有多種情況，因此是一個多項式分佈對應抽樣分佈P(θ)，對於多項式為抽樣分佈來說，狄利克雷分佈是它的共軛分佈。

先驗分佈反映了某種先驗資訊，後驗分佈既反映了先驗分佈提供的資訊，又反映了樣本提供的資訊。若先驗分佈和抽樣分佈決定的後驗分佈與先驗分佈是同類型分佈，則稱先驗分佈為抽樣分佈的共軛分佈。當先驗分佈與抽樣分佈共軛時，後驗分佈與先驗分佈屬於同一種類型，這意味著先驗資訊和樣本資訊提供的資訊具有一定的同一性。
- Beta的共軛分佈是伯努利分佈；
- 多項式分佈的共軛分佈是狄利克雷分佈；
- 高斯分佈的共軛分佈是高斯分佈。

那麼狄利克雷分佈什麼樣子？
先介紹Γ函式和B函式

Γ(x)=∫∞0tx−1e−tdtB(m,n)=Γ(m)Γ(n)Γ(m+n)

狄利克雷分佈為下圖，其中α1...αn就是每個型別的偽先驗（按照歷史經驗和常識，比如骰子每個面都出現10次）
這裡寫圖片描述

抽取模型

介紹完了基礎的數學知識，現在來看下如何得到LDA模型。
因為LDA是詞袋模型，各個主題，各個詞之間並沒有關聯，因此我們對於M篇文章，K個主題，可以兩次抽取，第一次抽取M個 topics 生成概率，第二次獲取K個主題的詞生成概率

主題生成概率

z⃗ 是topic主題向量
α⃗ 是在訓練時指定的引數
根據貝葉斯引數估計，可以得到主題的分佈概率如下

p(z⃗ |α⃗ )=∏m=1Mp(z⃗ m|α⃗ )=∏m=1MΔ(n⃗ m+α⃗ )Δ(α⃗ )(∗)

詞生成概率

p(w⃗ |z⃗ ,β⃗ ) 是在指定的主題z和給定的引數

相關推薦

LDA主題模型三連擊-入門/理論/程式碼

本文將從三個方面介紹LDA主題模型——整體概況、數學推導、動手實現。 關於LDA的文章網上已經有很多了，大多都是從經典的《LDA 數學八卦》中引出來的，原創性不太多。 本文將用盡量少的公式，跳過不需要的證明，將最核心需要學習的部分與大家分享

LDA主題模型三連擊-入門/理論/代碼

矩陣 ota 函數 dom 主題模型 估計 chart news span 本文將從三個方面介紹LDA主題模型——整體概況、數學推導、動手實現。 關於LDA的文章網上已經有很多了，大多都是從經典的《LDA 數學八卦》中引出來的，原創性不太多。 本文將用盡量少的公式，跳過不

【入門程式設計題】--2.級數求和與三連擊問題

1.級數求和問題 已知：S_n= 1+1/2+1/3+…+1/nSn​=1+1/2+1/3+…+1/n。顯然對於任意一個整數KK，當nn足夠大的時候，S_nSn​大於KK。 現給出一個整數KK（1 \le k \le 151≤k≤15），要求計算出一個最小的nn；使得S_n>KSn​&

Cocos2D-X2.2.3學習筆記8(處理精靈單擊、雙擊和三連擊事件)

屏幕 () rtu cati 輸出 public exit 什麽是 avi 我們依據上一次介紹的觸屏事件和事件隊列等知識來實現觸屏的單擊，雙擊，三連擊事件。 下圖為我們實現的效果圖： 單擊精靈跳躍一個高度， 雙擊精靈跳躍的高度比單擊的高 三連擊精靈跳躍的跟高

用scikit-learn學習LDA主題模型

大小 href 房子 鏈接 size 目標 文本 訓練樣本 papers 　　　　在LDA模型原理篇我們總結了LDA主題模型的原理，這裏我們就從應用的角度來使用scikit-learn來學習LDA主題模型。除了scikit-learn, 還有spark MLlib和gen

Spark機器學習(8)：LDA主題模型算法

算法 ets 思想 dir 骰子 cati em算法 第一個 不同 1. LDA基礎知識 LDA（Latent Dirichlet Allocation）是一種主題模型。LDA一個三層貝葉斯概率模型，包含詞、主題和文檔三層結構。 LDA是一個生成模型，可以用來生成一篇文

LDA主題模型

.com img png src 技術 nbsp ima blog com LDA主題模型

洛谷 P1618 三連擊（升級版）

span main 比例 pre color clu 輸出 std mut 題目描述 將1，2，…，9共9個數分成三組，分別組成三個三位數，且使這三個三位數的比例是A:B:C，試求出所有滿足條件的三個三位數，若無解，輸出“No!!!”

luogu P1008 三連擊

第一個 break 判斷 RM 註意 輸入 std () tdi 題目背景 本題為提交答案題，您可以寫程序或手算在本機上算出答案後，直接提交答案文本，也可提交答案生成程序。 題目描述 將1，2，…，9共9個數分成三組，分別組成三個三位數，且使這三個三位數構成1：2：3的比例

三連擊...（升級版）

ring 簡便 clas tdi color ++ for end cst 綜合了一下題解的，比較簡便。 1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm>

osu!三連擊

set long bottom code note ... 兩個 沒有 個數 P1654 OSU! 題目背景 原 《產品排序》 參見P2577 題目描述 osu 是一款群眾喜聞樂見的休閑軟件。 我們可以把osu的規則簡化與改編成以下的樣子: 一共有n次操作，

P1008三連擊

++ 是的 pac inf 計數 return main name .com 題解： 解法一： 暴力模擬每個三位數，如果三位數每個數字拆出來扔進數組裏的各個個數都正好是1，就成了。 解法二： 一開始肯定嘗試暴力，但這道題妙就妙在固定的九個數。取一個少一個，那麽我們就可以在

模板三連擊：樹狀陣列+線段樹+主席樹

沒事兒幹，複習模板...... 1.樹狀陣列 本來不想寫這個的，但是反正就幾分鐘就打完了，所以就寫了，水AC數。 洛谷 P3374 [模板]樹狀陣列 1 1 #include<cstdio> 2 3 typedef long long ll;

P1008_三連擊（JAVA語言）

/*  * 題目描述 將1,2,⋯,9共9個數分成3組， 分別組成3個三位數，且使這3個三位數構成1:2:3的比例，試求出所有滿足條件的3個三位數。 輸入輸出格式 輸入格式： 木有輸入 輸出格式： 若干行，每行3個數字。按照每行第1個數字升序排列。  */ publi

洛谷P1618 三連擊（升級版）

題目描述 將1，2，…，9共9個數分成三組，分別組成三個三位數，且使這三個三位數的比例是A:B:C，試求出所有滿足條件的三個三位數，若無解，輸出“No!!!”。 輸入格式： 三個數，A B C。 輸出格式： 若干行，每行3個數字。按照每行第一個數字升序排列。 輸入樣例#1：

洛谷—三連擊

  題目描述: 將1,2, \cdots ,91,2,⋯,9共99個數分成33組，分別組成33個三位數，且使這33個三位數構成1:2:31:2:3的比例，試求出所有滿足條件的33個三位數。 AC_CODE: #include<bits/stdc++.h> usi

LDA 主題模型 通俗簡單講解

https://algobeans.com/2015/06/21/laymans-explanation-of-topic-modeling-with-lda-2/ http://blog.echen.me/2011/08/22/introduction-to-latent-dirich

洛谷新手村p1008三連擊

P1008 三連擊 題目背景 本題為提交答案題，您可以寫程式或手算在本機上算出答案後，直接提交答案文字，也可提交答案生成程式。 題目描述 將1,2, \cdots ,91,2,⋯,9共99個數分成33組，分別組成33個三位數，且使這33個三位數構成1:2:31:2:3的比例，試求出所

LDA主題模型發展歷程(1)

** 主題模型發展歷程 **首先從Unigram model談起，基於Unigram model加入貝葉斯先驗得到貝葉斯Unigram model,再基於SVD分解得到LSA模型，在LSA模型的基礎上加入概率化的解釋，就得到了PLSA,在PLSA的基礎上加入先驗化的

自然語言處理-LDA主題模型

一、LDA主題模型簡介 LDA(Latent Dirichlet Allocation)中文翻譯為：潛在狄利克雷分佈。LDA主題模型是一種文件生成模型，是一種非監督機器學習技術。它認為一篇文件是有多個主題的，而每個主題又對應著不同的詞。一篇文件的構造過程，首先是以一定的概率