人群中多看了一眼

阿新 • • 發佈：2019-01-20

資料結構設計

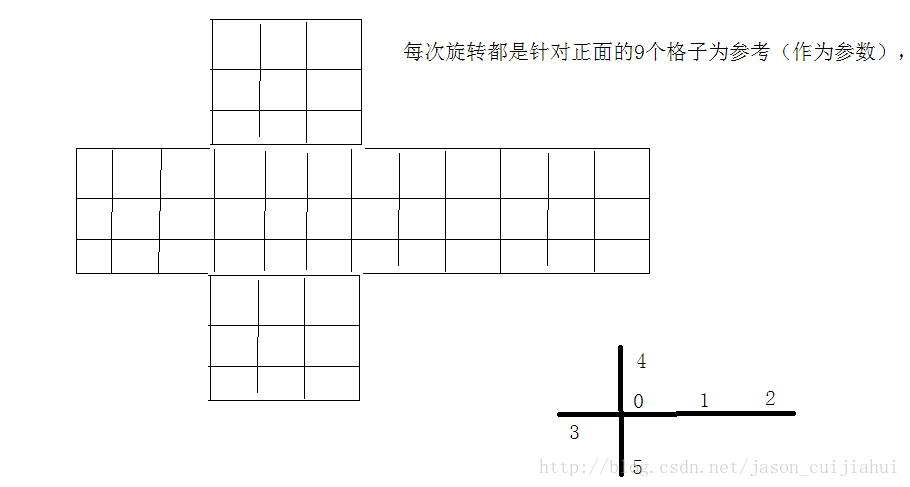
1.設計一個魔方（六面）的程式
思路：
把魔方從正面看展開成一個平面，如圖1所示。設計一個類，其中Spacexy[SPACE][LEN][LEN];中的SPACE為0~5表示六個面，每個數字代表哪一面見圖1.LEN為0~2，[LEN][LEN]表示某個面的3*3的9個格子。

類中的方法是根據展開的平面設計的，具體的某個面的某個格子由Spacexy[SPACE][LEN][LEN];定位。

注: [LEN][LEN] = [i][j] ；i, j按照矩陣的方式取
這裡寫圖片描述

實現：

#include<iostream>
using namespace std;

class 
 MagicCube{
    private:
        enum{LEN = 3, SPACE = 6};
        enum color{red, yellow, black, blue, green, purple};
        enum color Spacexy[SPACE][LEN][LEN];

    public:
        MagicCube();
        ~MagicCube(){ };
        void LeftRotate(int j);
        void UpRoate(int i);
        void PrintCube(); 
}; 

void 
 MagicCube::UpRoate(int j){
    color tmp[LEN];

    for(int i=0;i<LEN;i++)
        tmp[i] = Spacexy[0][i][j];

    // 0
    for(int i=0;i<LEN;i++)
        Spacexy[0][i][j] = Spacexy[5][i][j];

    // 5
    for(int i=0;i<LEN;i++)
        Spacexy[5]][i][j] = Spacexy[2][LEN-1-i][j];

    // 2
    for(int 
 i=0;i<LEN;i++)
        Spacexy[2][LEN-1-i][j] = Spacexy[4][i][j];

    // 4
    for(int i=0;i<LEN;i++)
        Spacexy[4][i][j] = tmp[i];

}

void MagicCube::LeftRotate(int i)
{
    color tmp[LEN];

    for(int j=0;j<LEN;j++)
        tmp[j] = Spacexy[0][i][j];

    // 0
    for(int j=0;j<LEN;j++)
        Spacexy[0][i][j] = Spacexy[1][i][j];

    // 1
    for(int j=0;j<LEN;j++)
        Spacexy[1][i][j] = Spacexy[2][i][j];

    // 2
    for(int j=0;j<LEN;j++)
        Spacexy[2][i][j] = Spacexy[3][i][j];

    // 3
    for(int j=0;i<LEN;j++)
        Spacexy[3][i][j] = tmp[j]; 
}

2.Serialize and Deserialize Binary Tree
題目：
Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.

Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.

For example, you may serialize the following tree

as “[1,2,3,null,null,4,5]”, just the same as how LeetCode OJ serializes a binary tree. You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.

實現：

// 我的版本比較蠢
#include <iostream>
#include <sstream>
#include <vector>
#include <queue>
#include <string>
using namespace std;

struct Node{
    int data;
    Node* left;
    Node* right;
};

string toString(const int& t) {
    ostringstream oss;
    oss<<t;
    return oss.str();
}

int toInt(const string& str) {
    istringstream iss(str);
    int num;
    iss >> num;
    return num;
}



string serialize(Node *root) {
    string result = "";
    if(root==NULL) return "";
    queue<Node*> record;
    record.push(root);
    while(!record.empty()) {
        Node* e = record.front();
        if(e==NULL) 
            result += "null,";
        else {
            result += toString(e->data)+",";
            record.push(e->left);
            record.push(e->right);
        }
        record.pop();
    }   
    return result;  
}

Node* CreateBinaryTree(vector<string> &a, int i, int n) {
    if(i>n-1 || a[i]=="null") return NULL;

    Node *p = new Node;
    p->data = toInt(a[i]);
    p->left = CreateBinaryTree(a, i*2+1, n);
    p->right = CreateBinaryTree(a, i*2+2, n);

    return p;
}

void SplitString(const string& s, vector<string>& v, const string& c)
{
    string::size_type pos1, pos2;
    pos2 = s.find(c);
    pos1 = 0;
    while(string::npos != pos2)
    {
        v.push_back(s.substr(pos1, pos2-pos1));

        pos1 = pos2 + c.size();
        pos2 = s.find(c, pos1);
    }
    if(pos1 != s.length())
        v.push_back(s.substr(pos1));
}

Node* deserialize(string data) {
    vector<string> sArr;    
    SplitString(data, sArr, ",");
    Node* root = CreateBinaryTree(sArr, 0, sArr.size());
    return root;    
}

int main() {
    Node *p1 = new Node;
    p1->data = 1;
    p1->left = NULL;
    p1->right = NULL;

    Node *p2 = new Node;
    p2->data = 2;
    p2->left = NULL;
    p2->right = NULL;

    p1->left = p2;

    string sResult = serialize(p1);
    cout<<serialize(p1)<<endl;
    deserialize(sResult);
    cout<<serialize(deserialize(serialize(p1)))<<endl;


    return 0;
}

// 別人的版本
class Codec {
public:
    // Encodes a tree to a single string.
    string serialize(TreeNode* root) {
        if (root == nullptr) return "#";
        return to_string(root->val)+","+serialize(root->left)+","+serialize(root->right);
    }

    // Decodes your encoded data to tree.
    TreeNode* deserialize(string data) {
        return mydeserialize(data);
    }
    TreeNode* mydeserialize(string& data) {
        if (data[0]=='#') {
            if(data.size() > 1) data = data.substr(2);
            return nullptr;
        } else {
            TreeNode* node = new TreeNode(helper(data));
            node->left = mydeserialize(data);
            node->right = mydeserialize(data);
            return node;
        }
    }
private:
    int helper(string& data) {
        int pos = data.find(',');
        int val = stoi(data.substr(0,pos));
        data = data.substr(pos+1);
        return val;
    }
};

大資料處理

1.多檔案頻率排序
題目：
有10個檔案，每個檔案1G，每個檔案的每一行存放的都是使用者的query，每個檔案的query都可能重複。要求按照query的頻度排序。
思路：
a) 方案1
1. 順序讀取10個檔案，按照hash(query)的結果將query寫入到另外10個檔案中。這樣新生成的檔案每個的大小大約也1G(假設hash函式是隨機的)。
2. 找一臺記憶體在2G左右的機器，依次對用hash_map(query, query_count)來統計每個query出現的次數。利用快速/堆/歸併排序按照出現次數進行排序。將排序好的query和對應的query_cout輸出到檔案中。這樣得到了10個排好序的檔案。
3. 對這10個檔案進行歸併排序(內排序與外排序相結合)。

b) 方案2：
一般query的總量是有限的，只是重複的次數比較多而已，可能對於所有的query，一次性就可以加入到記憶體了。這樣，我們就可以採用trie樹/hash_map等直接來統計每個query出現的次數，然後按出現次數做快速/堆/歸併排序就可以了。

c) 方案3：
與方案1類似，但在做完hash，分成多個檔案後，可以交給多個檔案來處理，採用分散式的架構來處理(比如MapReduce)，最後再進行合併。

演算法

樹結構

二叉樹

1.二叉樹層次遍歷
題目：
輸入一顆二元樹，從上往下按層列印樹的每個結點，同一層中按照從左往右的順序列印。

     8
    / \
   6   10
  / \  / \
 5   79   11

輸出：
8 6 10 5 7 9 11

思路：
用佇列，出隊列印，並壓入左右兒子。

實現：

struct Node{
    int data;
    Node* left;
    Node* right;
}
void levelPrint(Node* root){
    if(root==NULL) return;
    queue<Node*> record;
    record.push(root);
    while(!record.empty()){
        cout<<record.front()->data<<' ';
        if(record.front()->left!=NULL)
            record.push(record.front()->left);
        if(record.front()->right!=NULL)
            record.push(record.front()->right);
        record.pop();
    }
    cout<<endl;
}

2.映象二叉樹
題目：
請完成一個函式，輸入一個二叉樹，該函式輸出它的映象。

// 原二叉樹
     8
    / \
   6   10
  / \  / \
 5   79   11

// 映象二叉樹
     8
    / \
   10   6
  / \  / \
 11  97   5

二叉樹結點的定義如下：

struct BinaryTreeNode  
{  
    int data;  
    BinaryTreeNode *Left;  
    BinaryTreeNode *Right;  
};

思路：
遞迴思路：
把左子樹和右子樹變成映象子樹後，在把左右子樹的root相互交換。

迭代思路：
類似層次遍歷那種思路，不過用的是棧

實現：

// 遞迴實現
void Mirror(BinaryTreeNode *root){
    if(root==NULL) return;

    Mirror(root->Left);
    Mirror(root->Right);

    BinaryTreeNode *tmp = root->Left;
    root->Left = root->Right;
    root->Right = tmp;
}

// 迭代實現
// 這種相當於先序遍歷映象樹
void Mirror(BinaryTreeNode *root){
    stack<Node*> record;
    if(root!=NULL)
        record.push(root);
    while(!record.empty()){
        Node* tmproot = record.top();
        record.pop();

        if (tmproot->Left!=NULL)
            record.push(tmproot->Left);
        if (tmproot->Right!=NULL)
            record.push(tmproot->Right);

        Node* tmp = tmproot->Left;
        tmproot->Left = tmproot->Right;
        tmproot->Right = tmp;
    }
}

補充：
這個要寫個測試樣例。

3.求二叉樹中結點的最大距離
題目：
如果我們把二叉樹堪稱一個圖，父子結點之間的連線看成是雙向的。我們姑且定義“距離”為兩個結點之間的邊的個樹。求一棵二叉樹中相距最遠的兩個結點之間的邊的個樹。

思路：
可以用遞迴的思路去做，設父結點為F，左子樹為L，右子樹為R，則樹F相距最遠無非有這三種可能：

樹L相距最遠
樹R相距最遠
樹L到結點F的最長距離+1+樹R到結點F的最長距離

實現：

struct BinaryTreeNode  
{  
    int data;  
    BinaryTreeNode *Left;  
    BinaryTreeNode *Right;  
};

int TreeMaxLength(BinaryTreeNode *root, int &depth){
    int ld, rd;
    if(root==NULL){
        depth = 0;
        return 0;
    }
    lm = TreeMaxLength(root->Left, ld);
    rm = TreeMaxLength(root->Right, rd);
    depth = (ld>rd?ld:rd)+1;
    // bridge是邊的條數而不是結點的個數
    int bridge = ld+rd;
    int tmp = lm>rm?lm:rm;
    return (tmp>bridge?tmp:bridge);

}

4.從陣列生成一棵二叉樹
實現：

#include<iostream>
using namespace std;
struct TreeNode  
{  
  TreeNode *left;  
  TreeNode *right;  
  int val;  
  TreeNode(int x=0)  
   : val(x), left(NULL), right(NULL){}  
};  

TreeNode* CreateBinaryTree(int a[], int i, int n){
    // 陣列中的值-1代表結點null
    if(i>n-1 || a[i]==-1) return NULL;

    TreeNode *p = new TreeNode(a[i]);
    p->left = CreateBinaryTree(a, i*2+1, n);
    p->right = CreateBinaryTree(a, i*2+2, n);
    return p;
}

void Destory(TreeNode *root){
    if(root==NULL) return ;
    Destory(root->left);
    Destory(root->right);
    delete root;
}

5.列印一棵二叉樹
實現：

#include <cmath>  
#include <iostream>  
#include <vector>  
using namespace std;
//using std::vector;  
//using std::cout;  
//using std::endl;  
//using std::max;  

void PrintBinaryTree(TreeNode *root);  

struct TreeNode  
{  
  TreeNode *left;  
  TreeNode *right;  
  int val;  
  TreeNode(int x=0)  
   : val(x), left(NULL), right(NULL){}  
};  

static int MaxLevel(TreeNode *root)  
{  
  if(root == NULL) return 0;  
  return max(MaxLevel(root->left), MaxLevel(root->right)) + 1;  
}  

// test whether all elements in vector are NULL  
static bool IsAllElementsNULL(const vector<TreeNode*> &nodes)  
{  
  vector<TreeNode*>::const_iterator it = nodes.begin();  

  while(it != nodes.end()){  
    if(*it) return false;   
    ++it;  
  }  
  return true;  
}  

static void PrintWhiteSpaces(int num)  
{  
  for(int i=0; i<num; ++i)  
    cout << " ";  
}  

void PrintNode(vector<TreeNode*> &nodes, int level, int max_level)  
{  
  if(nodes.empty() || IsAllElementsNULL(nodes)) return; // exit  

  int floor = max_level - level;  
  int endge_lines = 1 << (max(floor-1, 0));  
  int first_spaces = (1 << floor) - 1;  
  int between_spaces = (1 << (floor+1)) - 1;  

  PrintWhiteSpaces(first_spaces);  

  // print the 'level' level   
  vector<TreeNode*> new_nodes;  
  vector<TreeNode*>::const_iterator it = nodes.begin();  
  for(; it != nodes.end(); ++it){  
    if(*it != NULL){  
      cout << (*it)->val;  
      new_nodes.push_back((*it)->left);  
      new_nodes.push_back((*it)->right);  
    }  
    else{  
      new_nodes.push_back(NULL);  
      new_nodes.push_back(NULL);  
      cout << " ";  
    }  
    PrintWhiteSpaces(between_spaces);  
  }  
  cout << endl;  

  // print the following /s and \s  
  for(int i=1; i<= endge_lines; ++i){  
    for(int j=0; j<nodes.size(); ++j){  
      PrintWhiteSpaces(first_spaces - i);  
      if(nodes[j] == NULL){  
        PrintWhiteSpaces(endge_lines + endge_lines + i + 1);  
        continue;  
      }  
      if(nodes[j]->left != NULL)  
        cout << "/";  
      else  
        PrintWhiteSpaces(1);  

      PrintWhiteSpaces(i+i-1);  

      if(nodes[j]->right != NULL)  
        cout << "\\";  
      else  
        PrintWhiteSpaces(1);  

      PrintWhiteSpaces(endge_lines + endge_lines - i);  
    }  
    cout << endl;  
  }  

  PrintNode(new_nodes, level+1, max_level);  

}  

// wrapper function  
void PrintBinaryTree(TreeNode *root)  
{  
  int max_level = MaxLevel(root);  
  vector<TreeNode*> nodes;  

  nodes.push_back(root);  

  PrintNode(nodes, 1, max_level);  
}

int main()  
{  
  TreeNode *root(NULL);  

  root = new TreeNode(1);  
  root->left = new TreeNode(2);  
  root->right = new TreeNode(3);  

  root->left->left = new TreeNode(4);  
  root->right->right = new TreeNode(7);  

  root->left->left->left = new TreeNode(8);  
  root->left->left->right = new TreeNode(9);  
  PrintBinaryTree(root);  

  // root = Destroy(root);  
  return 0;  
}

6.非遞迴實現二叉樹的前序中序後序遍歷
實現：
遞迴前序遍歷

void preorderRecursive(TreeNode *node){
    if(node == NULL) return;
    visit(node);
    preorderRecursive(node->left);
    preorderRecursive(node->right);
}

非遞迴前序遍歷，用棧

void preorderRecursive(TreeNode *node){
    stack<TreeNode*> s;
    if(node!=NULL) s.push(node);
    while(!s.empty()){
        TreeNode *tmp = s.top();
        s.pop();
        visit(tmp);    
        if(tmp->right!=NULL) s.push(tmp->right);
        if(tmp->left!=NULL) s.push(tmp->left);
    }

}

非遞迴中序遍歷，沒有左結點，則對結點進行訪問

void inorderRecursive(TreeNode *node){
    stack<TreeNode*> s;
    TreeNode *tmp = node;
    while(!s.empty() || tmp!=NULL){
        if(tmp!=NULL){
            s.push(tmp);
            tmp = tmp->left;
        }
        else{
            tmp = s.top();
            s.pop();
            visit(tmp);  
            tmp = tmp->right;
        }
    }
}

非遞迴後序遍歷，利用非遞迴前序遍歷進行轉化

void postorderRecursive(TreeNode *node){
    stack<TreeNode *> sTraverse, sVisit;
    if(node!=NULL) sTraverse.push(node);
    while(!sTraverse.empty()){
        Node *tmp = sTraverse.top();
        sTraverse.pop();
        sVisit.push(tmp);
        // 先右結點
        if(tmp->right != NULL) tmp = tmp->right;
        // 後左結點
        if(tmp->left != NULL) tmp = tmp->left;
    }
    while(!sVisit.empty()){
        visit(sVisit.top());
        sVisit.pop();
    }
}

7.二叉樹的深度
題目：輸入一棵二叉樹的根結點，求該樹的深度。

實現：

#include<iostream>
using namespace std;
struct TreeNode  
{  
  TreeNode *left;  
  TreeNode *right;  
  int val;  
  TreeNode(int x=0)  
   : val(x), left(NULL), right(NULL){}  
};  

// 核心程式碼 
void searchDepth(TreeNode *root, int depth, int &maxDepth){
    if(root==NULL){
        if(depth>maxDepth)
            maxDepth = depth;
        return;
    }   

    searchDepth(root->left, depth+1, maxDepth);
    searchDepth(root->right, depth+1, maxDepth);

}

// 測試程式碼 
TreeNode* CreateBinaryTree(int a[], int i, int n){
    // 陣列中的值-1代表結點null
    if(i>n-1 || a[i]==-1) return NULL;

    TreeNode *p = new TreeNode(a[i]);
    p->left = CreateBinaryTree(a, i*2+1, n);
    p->right = CreateBinaryTree(a, i*2+2, n);
    return p;
}

void Destory(TreeNode *root){
    if(root==NULL) return ;
    Destory(root->left);
    Destory(root->right);
    delete root;
}



int main(){
    int tree[] = {10, 6, 14, 4, -1, -1, 16, -1, 3};
    TreeNode* root = CreateBinaryTree(tree, 0, 9);
    int max = 0;
    searchDepth(root, 0, max);
    cout<<max<<endl;
    Destory(root);
    return 0;
}

8.二叉樹兩個結點的最低共同父結點（LCP）
題目：
輸入二叉樹中的兩個結點，輸出這兩個結點在數中最低的共同父結點。

思路（遞迴）：
1. 在左子樹查詢目標物件
2. 在右子樹查詢目標物件

a) 如果在左子樹中什麼都沒找到，則表明都在右子樹上，然後LCP是最早查詢的目標物件
b) 如果在左子樹中什麼都沒找到，則表明都在右子樹上，然後LCP是最早查詢的目標物件
c) 如果在左右子樹各找到一個，則表明LCP是根結點

實現：

#include<iostream>
using namespace std;
struct TreeNode  
{  
  TreeNode *left;  
  TreeNode *right;  
  int val;  
  TreeNode(int x=0)  
   : val(x), left(NULL), right(NULL){}  
};  

TreeNode* CreateBinaryTree(int a[], int i, int n){
    // 陣列中的值-1代表結點null
    if(i>n-1 || a[i]==-1) return NULL;

    TreeNode *p = new TreeNode(a[i]);
    p->left = CreateBinaryTree(a, i*2+1, n);
    p->right = CreateBinaryTree(a, i*2+2, n);
    return p;
}

void Destory(TreeNode *root){
    if(root==NULL) return ;
    Destory(root->left);
    Destory(root->right);
    delete root;
}


TreeNode* GetLCP(TreeNode *root, TreeNode *n1, TreeNode *n2){
    if(root==NULL || n1==NULL || n2==NULL) return NULL;
    if(n1==root || n2==root) return root;
    // 在左子樹上找n1或n2 
    TreeNode* leftSub = GetLCP(root->left, n1, n2);

    // 在右子樹上找n1或n2 
    TreeNode* rightSub = GetLCP(root->right, n1, n2);

    if(leftSub==NULL){// n1和n2都不能在左子樹找到，則返回右子樹中率先遇到n1或n2的結點
        return rightSub; 
    }
    else if(rightSub==NULL){
        return leftSub;
    }
    else{// n1和n2分別在左右子樹上，所以返回根結點 
        return root;
    }
} 

int main(){
    int arr[] = {1, 2, 3, 4, 5, 6, 7, 8};
    TreeNode *root = CreateBinaryTree(arr, 0, 8);
    /*
              1
          2      3
       4    5 6    7
    8

    */


    TreeNode *n1 = root->left->left->left;
    TreeNode *n2 = root->left->right;

    TreeNode *result = GetLCP(root, n1, n2);
    cout<<result->val<<endl;

    Destory(root);
}

9.Binary Tree Zigzag Level Order Traversal
題目：
Given a binary tree, return the zigzag level order traversal of its nodes’ values. (ie, from left to right, then right to left for the next level and alternate between).

For example:
Given binary tree [3,9,20,null,null,15,7],

return its zigzag level order traversal as:

[
  [3],
  [20,9],
  [15,7]
]

實現：

#include<iostream>
#include<stack>
#include<queue>
using namespace std;

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

void zigzagLevelOrder(TreeNode* root) {
    queue<TreeNode*> r1;
    stack<TreeNode*> r2;
    r1.push(root);
    while(r1.empty()==false || r2.empty()==false) {
        while(!r1.empty()) {
            TreeNode* e = r1.front();
            cout<<e->val<<" ";
            if(e->left!=NULL) r2.push(e->left);
            if(e->right!=NULL) r2.push(e->right);
            r1.pop();
        }
        cout<<endl;
        while(!r2.empty()) {
            TreeNode* e = r2.top();
            cout<<e->val<<" ";
            if(e->left!=NULL) r1.push(e->left);
            if(e->right!=NULL) r1.push(e->right);
            r2.pop();           
        }
        cout<<endl;
    }           
}

int main() {
    TreeNode *n1 = new TreeNode(3);
    TreeNode *n2 = new TreeNode(9);
    TreeNode *n3 = new TreeNode(20);
    TreeNode *n4 = new TreeNode(15);
    TreeNode *n5 = new TreeNode(7);

    n1->left = n2;
    n1->right = n3;
    n3->left = n4;
    n3->right = n5;

    zigzagLevelOrder(n1);
}

10.Construct Binary Tree from Preorder and Inorder Traversal
題目：
Given preorder and inorder traversal of a tree, construct the binary tree.

Note:
You may assume that duplicates do not exist in the tree.

For example, given

preorder = [3,9,20,15,7]
inorder = [9,3,15,20,7]
Return the following binary tree:

思路
實現：

#include<iostream>
#include<vector>
using namespace std;

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(-1), left(NULL), right(NULL) {}
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

TreeNode* helper(vector<int>& preorder, int preI, int preJ, vector<int>& inorder, int inI, int inJ) {
    if(preI > preJ || inI > inJ) return NULL;
    int rootVal = preorder[preI];
    int rootIndex = 0;
    for(int i=inI;i<=inJ;i++) {
        if(inorder[i] == rootVal) {
            rootIndex = i;
            break;
        }
    }

    TreeNode* newNode = new TreeNode(rootVal);
    int lLen = rootIndex - inI;
    int rLen = inJ - rootIndex;
    newNode->left = helper(preorder, preI+1, preI+lLen, inorder, inI, rootIndex-1);
    newNode->right = helper(preorder, preI+lLen+1, preJ, inorder, rootIndex+1, inJ);

    return newNode;
}


TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
    return helper(preorder, 0, preorder.size()-1, inorder, 0, inorder.size()-1);
}



// 列印二叉樹
TreeNode* Array2BinaryTree(int arr[], int i, int j){
    if(i>j) return NULL;
    int mid = (i+j)/2;
    TreeNode* root = new TreeNode;
    root->val = arr[mid];
    root->left = Array2BinaryTree(arr, i, mid-1);
    root->right = Array2BinaryTree(arr, mid+1, j);
    return root;
}

// 列印二叉樹
void PrintBinaryTree(TreeNode *root);  



static int MaxLevel(TreeNode *root)  
{  
  if(root == NULL) return 0;  
  return max(MaxLevel(root->left), MaxLevel(root->right)) + 1;  
}  

// test whether all elements in vector are NULL  
static bool IsAllElementsNULL(const vector<TreeNode*> &nodes)  
{  
  vector<TreeNode*>::const_iterator it = nodes.begin();  

  while(it != nodes.end()){  
    if(*it) return false;   
    ++it;  
  }  
  return true;  
}  

static void PrintWhiteSpaces(int num)  
{  
  for(int i=0; i<num; ++i)  
    cout << " ";  
}  

void PrintNode(vector<TreeNode*> &nodes, int level, int max_level)  
{  
  if(nodes.empty() || IsAllElementsNULL(nodes)) return; // exit  

  int floor = max_level - level;  
  int endge_lines = 1 << (max(floor-1, 0));  
  int first_spaces = (1 << floor) - 1;  
  int between_spaces = (1 << (floor+1)) - 1;  

  PrintWhiteSpaces(first_spaces);  

  // print the 'level' level   
  vector<TreeNode*> new_nodes;  
  vector<TreeNode*>::const_iterator it = nodes.begin();  
  for(; it != nodes.end(); ++it){  
    if(*it != NULL){  
      cout << (*it)->val;  
      new_nodes.push_back((*it)->left);  
      new_nodes.push_back((*it)->right);  
    }  
    else{  
      new_nodes.push_back(NULL);  
      new_nodes.push_back(NULL);  
      cout << " ";  
    }  
    PrintWhiteSpaces(between_spaces);  
  }  
  cout << endl;  

  // print the following /s and \s  
  for(int i=1; i<= endge_lines; ++i){  
    for(int j=0; j<nodes.size(); ++j){  
      PrintWhiteSpaces(first_spaces - i);  
      if(nodes[j] == NULL){  
        PrintWhiteSpaces(endge_lines + endge_lines + i + 1);  
        continue;  
      }  
      if(nodes[j]->left != NULL)  
        cout << "/";  
      else  
        PrintWhiteSpaces(1);  

      PrintWhiteSpaces(i+i-1);  

      if(nodes[j]->right != NULL)  
        cout << "\\";  
      else  
        PrintWhiteSpaces(1);  

      PrintWhiteSpaces(endge_lines + endge_lines - i);  
    }  
    cout << endl;  
  }  

  PrintNode(new_nodes, level+1, max_level);  

}  

// wrapper function  
void PrintBinaryTree(TreeNode *root)  
{  
  int max_level = MaxLevel(root);  
  vector<TreeNode*> nodes;  

  nodes.push_back(root);  

  PrintNode(nodes, 1, max_level);  
} 

int main() {
    int preArr[] = {3, 9, 20, 15, 7};
    int inArr[] = {9, 3, 15, 20, 7};
    vector<int> preorder(preArr, preArr+5);
    vector<int> inorder(inArr, inArr+5);
    TreeNode* root = buildTree(preorder, inorder);
    PrintBinaryTree(root);

    return 0; 
}

二叉查詢樹

1.把一個有序整數陣列轉化為二叉查詢樹

思路：

#include<iostream>
#include<vector>
using namespace std;

struct TreeNode  
{  
  TreeNode *left;  
  TreeNode *right;  
  int val;  
  TreeNode(int x=0)  
   : val(x), left(NULL), right(NULL){}  
};  

TreeNode* Array2BinaryTree(int arr[], int i, int j){
    if(i>j) return NULL;
    int mid = (i+j)/2;
    TreeNode* root = new TreeNode;
    root->val = arr[mid];
    root->left = Array2BinaryTree(arr, i, mid-1);
    root->right = Array2BinaryTree(arr, mid+1, j);
    return root;
}

// 列印二叉樹
void PrintBinaryTree(TreeNode *root);  



static int MaxLevel(TreeNode *root)  
{  
  if(root == NULL) return 0;  
  return max(MaxLevel(root->left), MaxLevel(root->right)) + 1;  
}  

// test whether all elements in vector are NULL  
static bool IsAllElementsNULL(const vector<TreeNode*> &nodes)  
{  
  vector<TreeNode*>::const_iterator it = nodes.begin();  

  while(it != nodes.end()){  
    if(*it) return false;   
    ++it;  
  }  
  return true;  
}  

static void PrintWhiteSpaces(int num)  
{  
  for(int i=0; i<num; ++i)  
    cout << " ";  
}  

void PrintNode(vector<TreeNode*> &nodes, int level, int max_level)  
{  
  if(nodes.empty() || IsAllElementsNULL(nodes)) return; // exit  

  int floor = max_level - level;  
  int endge_lines = 1 << (max(floor-1, 0));  
  int first_spaces = (1 << floor) - 1;  
  int between_spaces = (1 << (floor+1)) - 1;  

  PrintWhiteSpaces(first_spaces);  

  // print the 'level' level   
  vector<TreeNode*> new_nodes;  
  vector<TreeNode*>::const_iterator it = nodes.begin();  
  for(; it != nodes.end(); ++it){  
    if(*it != NULL){  
      cout << (*it)->val;  
      new_nodes.push_back((*it)->left);  
      new_nodes.push_back((*it)->right);  
    }  
    else{  
      new_nodes.push_back(NULL);  
      new_nodes.push_back(NULL);  
      cout << " ";  
    }  
    PrintWhiteSpaces(between_spaces);  
  }  
  cout << endl;  

  // print the following /s and \s  
  for(int i=1; i<= endge_lines; ++i){  
    for(int j=0; j<nodes.size(); ++j){  
      PrintWhiteSpaces(first_spaces - i);  
      if(nodes[j] == NULL){  
        PrintWhiteSpaces(endge_lines + endge_lines + i + 1);  
        continue;  
      }  
      if(nodes[j]->left != NULL)  
        cout << "/";  
      else  
        PrintWhiteSpaces(1);  

      PrintWhiteSpaces(i+i-1);  

      if(nodes[j]->right != NULL)  
        cout << "\\";  
      else  
        PrintWhiteSpaces(1);  

      PrintWhiteSpaces(endge_lines + endge_lines - i);  
    }  
    cout << endl;  
  }  

  PrintNode(new_nodes, level+1, max_level);  

}  

// wrapper function  
void PrintBinaryTree(TreeNode *root)  
{  
  int max_level = MaxLevel(root);  
  vector<TreeNode*> nodes;  

  nodes.push_back(root);  

  PrintNode(nodes, 1, max_level);  
}


int main(){
    int test1[] = {1, 2, 3, 4, 5};
    int test2[] = {1, 2, 3, 4, 5, 6};
    TreeNode *root1 = Array2BinaryTree(test1, 0, 4);
    PrintBinaryTree(root1);

    TreeNode *root2 = Array2BinaryTree(test2, 0, 5);
    PrintBinaryTree(root2); 
    return 0;
}

其他：
非遞迴實現。

堆

1.隊伍晉級
題目：
n 支隊伍比賽，分別編號為 0, 1, 2, …, n-1，已知它們之間的實力對比關係，
儲存在一個二維陣列 w[n][n]中，w[i][j] 的值代表編號為 i，j 的隊伍中更強的一支。
所以 w[i][j]=i 或者 j，現在給出它們的出場順序，並存儲在陣列 order[n]中，
比如 order[n] = {4, 3, 5, 8, 1……}，那麼第一輪比賽就是 4 對 3， 5 對 8，…….
勝者晉級，敗者淘汰，同一輪淘汰的所有隊伍排名不再細分，即可以隨便排，
下一輪由上一輪的勝者按照順序，再依次兩兩比，比如可能是 4 對 5,直至出現第一名
程式設計實現，給出二

人群中多看了一眼

資料結構設計

大資料處理

演算法

樹結構

二叉樹

二叉查詢樹

堆

人群中多看了一眼

只是因為在人群中多看了你一眼.......

【春華秋實】.NET Core之只是多看了你一眼

每日踩坑 2018-11-26 MVC Razor ActionLink 生成的URL中多生成了一個引數 ?length=n

朋友融資了，給我看了一眼他們價值1個億的Go AI 程式碼

RESTful轉載，多看幾遍就理解了寫點自己的看法和理解

Ant在Java項目中的使用（一眼就看會）

JAVA中的深復制和淺復制--建議多看幾遍

無意中知道了我學網並簡單看了一下

ovs加dpdk在日誌中查看更多運行細節的方法

看了這麽多天後對libevent的理解

eclipse中Tomcat啟動了但看不到tomcat首頁

java中多執行緒一定快嗎?看完就知道!!!

Java長見到的面試題，看你能答出幾題，就知道自己有多菜了

Spark中的Spark Shuffle詳解(多看幾遍)

看了多遍博文采取幾遍結合，記錄一下Win7下Python與Tensorflow-CPU版開發環境的安裝與配置過程

Mozilla在Thunderbird 60.3中的修補了多個安全漏洞

MySQL 中的行級鎖、表級鎖和頁級鎖（不看後悔，看了必懂）

現在做前端的人那麼多，好的前端工資到底有多高，看了這個圖，當場說不出話！

蘋果稽核ipv6到底有多坑？看了你會少走很多路。

人群中多看了一眼

資料結構設計

大資料處理

演算法

樹結構

二叉樹

二叉查詢樹

堆

相關推薦