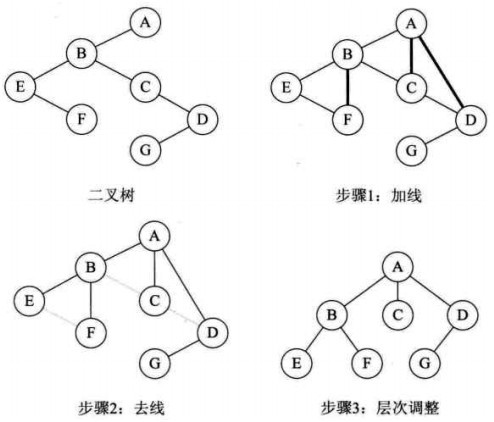
一般樹與二叉樹的相互轉換
一般來說,直接對一般樹做一些相關操作非常對不方便。因此,將一般樹轉換為二叉樹,操作完成後逆轉為一般樹成為了大部分人對付一般樹的方法。
一般樹轉換二叉樹:
1)將每一個結點與他的兄弟結點之間連一條線。
2)對每一個雙親結點,只保留它與第一個子結點的連線,刪除與其餘結點的連線。
3)整理,左右擺齊。
a a a a
/ | \ / | \ / /
b c d b...c...d b..c..d b
/ / \ -> / / \ -> / / -> / \
e f g e f....g e f..g e c
| | | / \
h h h f d
/ \
h g
二叉樹轉換一般樹(相反):
1)若一個結點是其父結點的左結點,則將此結點的右結點,右結點的右結點。。。都與其父結點相連線。
2)刪除原二叉樹所有父結點與右結點的連線。
圖示:
3)整理連線,統一高度。
相關推薦
一般樹與二叉樹的相互轉換
一般來說,直接對一般樹做一些相關操作非常對不方便。因此,將一般樹轉換為二叉樹,操作完成後逆轉為一般樹成為了大部分人對付一般樹的方法。 一般樹轉換二叉樹: 1)將每一個結點與他的兄弟結點之間連一條線。
森林、樹與二叉樹相互轉換
節點 png http 所有 相互轉換 層次 二叉樹 根節點 images 1、森林轉二叉樹 (1)、把每棵樹轉換為二叉樹 (2)、第一棵二叉樹不動,從第二棵二叉樹開始,一次把後一棵二叉樹的根結點作為前一棵二叉樹的根結點的右孩子,用線連接起來。
c++樹及樹與二叉樹的轉換
此演算法中的樹結構為“左兒子有兄弟連結結構” 在這樣的一個二叉樹中,一個節點的左分支是他的大兒子節點,右分支為他的大兄弟節點。 這裡講的樹有遞迴前根,中根,後根遍歷,插入節點,插入兄弟節點,查詢結點,釋放記憶體這些功能。 重點說一下查詢節點這一演算法: pSTreeNode CTree::Search
樹與二叉樹的轉換、樹的遍歷
樹和二叉樹不同,可以有0到n個孩子,所以實現起來很麻煩,但我們可以藉助樹的孩子兄弟表示法把樹轉換成二叉樹。 在孩子兄弟表示法中,某個結點的第一個孩子結點的指標是二叉樹中其左孩子結點指標,右兄弟結點指標是二叉樹中右孩子結點指標。 樹轉換為二叉樹過程: (1)樹中所有相同雙親結
3、非線性結構--樹與二叉樹——數據結構【基礎篇】
位置 enter 深度 基礎 表達式 左右 -a 基礎篇 先序遍歷 非線性結構--樹與二叉樹 二叉樹的基礎知識: 二叉樹的特點: 1、每個結點的度<=2 2、二叉樹是有序樹 二叉樹的五種不
樹與二叉樹(一)
color i++ add 表示 popu pop finished 不能 http 樹 定義 樹是n(n≥0)個結點的有限集,它或為空樹(n=0)。或為非空樹 非空樹T滿足下面條件: (1) 有且僅有一個稱為根的結點; (2)
樹與二叉樹(數據結構)
二叉樹 n+1 -s 不能 完美性 -1 平衡二叉樹 編號 大於 (1)樹的基本性質 1.樹中的結點數等於所有結點的度數+1。 2.樹中結點的最大度數稱為樹的度。 3.度為m的樹中第i層上至多有mi-1個結點。 4.高度為h的m叉樹至多有(mh-1)/(m-1)個結點。
樹與二叉樹——定義
color 二叉 來源 col tree round 描述 目錄 樹和二叉樹 樹形結構是一類重要的非線性結構數據結構。其中以樹和二叉樹最為常用,直觀看來,樹是以分支關系定義的層次結構。 樹的定義與基本術語 樹的結構定義是一個遞歸定義,即在樹的定義中又用到樹的概念。除了樹
普通樹與二叉樹
分享 != log 基本 while 要求 鏈式存儲 遞歸 樹節點 樹 樹作為一種常用的數據結構,不可不知。樹采用的是鏈式存儲,在詳細介紹樹之前要先了解幾個基本概念: 根、節點、孩子、雙親、兄弟、分支 就不多BB了,葉子指的是沒有子節點的節點,樹的高度指從根到樹所有葉子節點
數據結構——第五章 樹與二叉樹
http alt 個數 一對多 技術分享 info 圖片 blog inf 樹是一對多的結構 結點:樹的小圓圈 度:結點有多少個分叉 葉子結點:結點的度為0 雙親:parent 孩子:child 二叉樹:樹的度不超過2 滿二叉樹:每一層都是滿的 完全二叉
數據結構2 樹與二叉樹
post reat 訪問 tps 輸出 tvp aic -type sps 1.樹結構是一種非常重要的非線性結構,該結構中的一個數據元素可以有兩個或兩個以上的直接後繼元素,樹可以用來描述客觀世界中廣泛存在的層次結構關系。 2. 樹本身是遞歸的,即一棵樹由若幹顆子樹構成,而
實驗五:樹與二叉樹的實驗二
一、實驗目的 1、 熟練理解樹和二叉樹的相關概念,掌握的儲存結構和相關操作實現; 2、 掌握樹的順序結構的實現; 3、 學會運用樹的知識解決實際問題 二、實驗內容 1、自己確定一個二叉樹(樹結點型別、數目和結構自定)利用鏈式儲存結構方法儲存。實 現樹的構造,並完成: 1) 用前序
實驗四:樹與二叉樹的實驗一
一、實驗目的1、 熟練理解樹和二叉樹的相關概念,掌握的儲存結構和相關操作實現;2、 掌握樹的順序結構的實現;3、 學會運用樹的知識解決實際問題二、實驗內容 自己確定一個二叉樹(樹結點型別、數目和結構自定)利用順序結構方法儲存。實現樹的構造,並完成:1) 層序輸出結點資料;2) 以合理的格式
Android版資料結構與演算法(六):樹與二叉樹
/** * 前序遍歷——迭代 * @author Administrator * */ public void preOrder(TreeNode node){ if(node == null){ return;
資料結構之樹與二叉樹(下)
上面兩篇我們瞭解了樹的基本概念以及二叉樹的遍歷演算法,還對二叉查詢樹進行了模擬實現。數學表示式求值是程式設計語言編譯中的一個基本問題,表示式求值是棧應用的一個典型案例,表示式分為字首、中綴和字尾三種形式。這裡,我們通過一個四則運算的應用場景,藉助二叉樹來幫助求解表
樹與二叉樹5之B樹、B+樹及R樹
動態查詢樹主要有:二叉查詢樹(Binary Search Tree),平衡二叉查詢樹(Balanced Binary Search Tree),紅黑樹(Red-Black Tree ),B-tree/B+-tree/ B*-tree (B~Tree)。前三者是典型的二叉查詢樹
【資料結構與演算法】002—樹與二叉樹(Python)
概念 樹 樹是一類重要的非線性資料結構,是以分支關係定義的層次結構 定義: 樹(tree)是n(n>0)個結點的有限集T,其中: 有且僅有一個特定的結點,稱為樹的根(root) 當n>1時,其餘結點可分為m(m>0)個互不相交的有限集T1,T2,……Tm,其中每一個集合本身又是一棵
樹與二叉樹(C語言)
1. 儲存結構 1.1 順序儲存結構 1.2 鏈式儲存結構 typedef strcture BTNode { char data; struct BTNode *lchild; struct BTNode *rchild; }BTNode;
資料結構樹與二叉樹例題
樹與二叉樹例題 例1 高度為K(K>=2)的完全二叉樹至少有()個葉子結點。 解: 根據二叉樹性質 二叉樹第i(i>=1)層上至多有2^(i-1)個結點 第K-1層有 2^(K-1-1)=2^(K-2) 個結點 求二叉樹至少有多
樹與二叉樹
樹形結構是計算機最重要的資料結構,連結串列示特殊的樹. 特點: 節點抽象為集合,邊抽象為關係。 樹由節點與邊構成。 子節點之間是沒有交集的。 每個節點的指標域兩個至多個(N叉樹)。 節點數 = 邊數 + 1。 圖的度 = 出度 + 入度, 樹的度 =