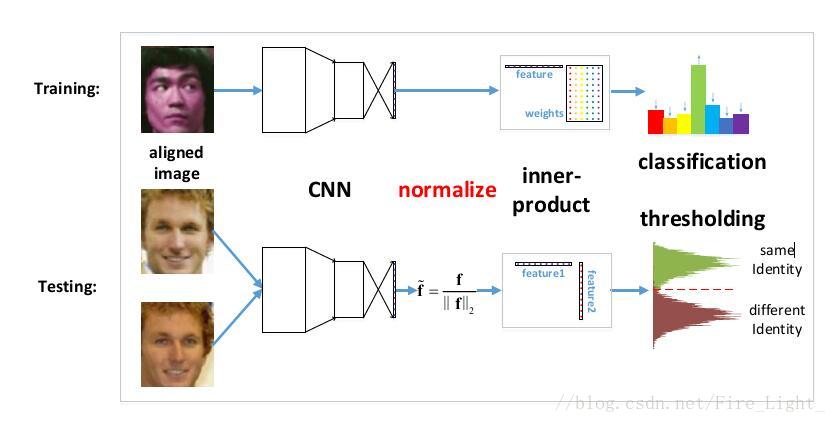
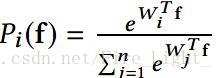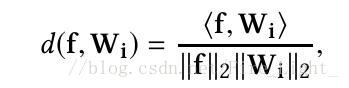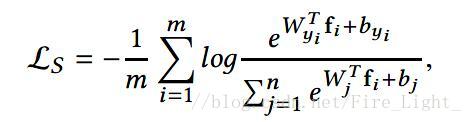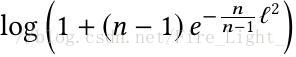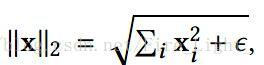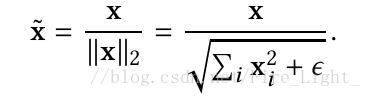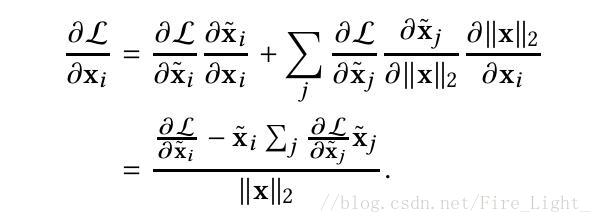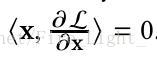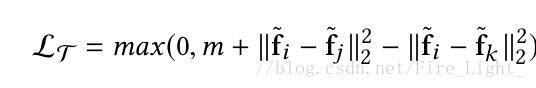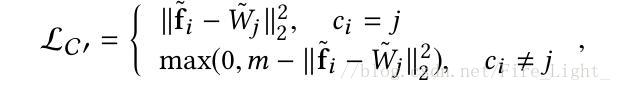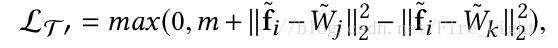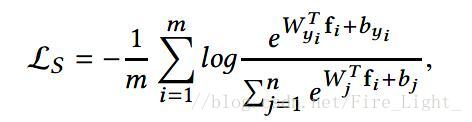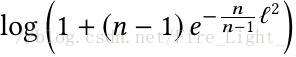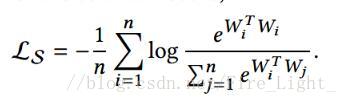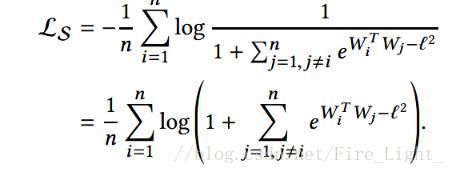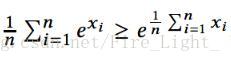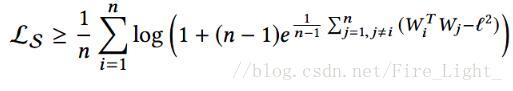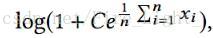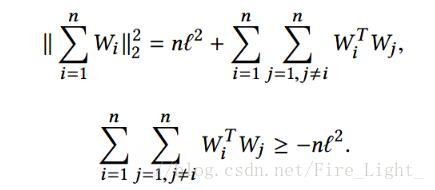人臉識別系列(十四):NormFace
提出問題
之前的人臉識別工作,在特徵比較階段,通常使用的都是特徵的餘弦距離

而餘弦距離等價於L2歸一化後的內積,也等價L2歸一化後的歐式距離(歐式距離表示超球面上的弦長,兩個向量之間的夾角越大,弦長也越大)
然而,在實際上訓練的時候用的都是沒有L2歸一化的內積
關於這一點可以這樣解釋,Softmax函式是:
可以理解為和特徵向量x的內積越大,x屬於第k類概率也就越大,訓練過程就是最大化x與其標籤對應項的權值的過程。
這也就是說在訓練時使用的距離度量與在測試時使用的度量是不一樣的。
測試時是否需要歸一化?
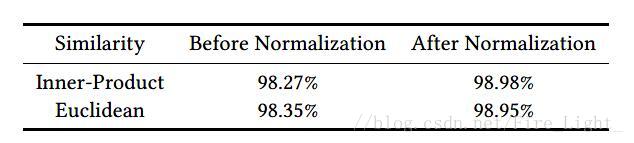
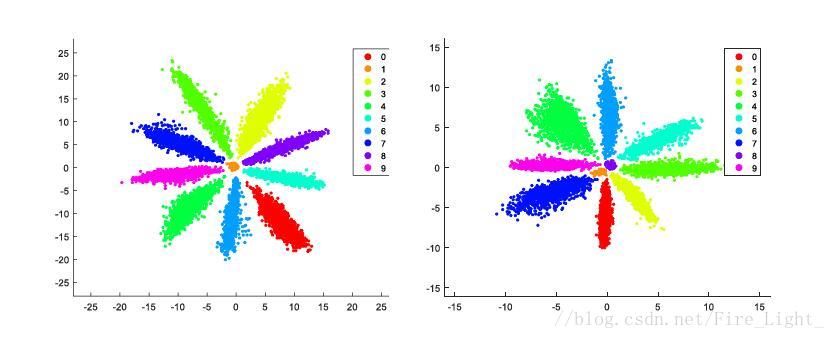
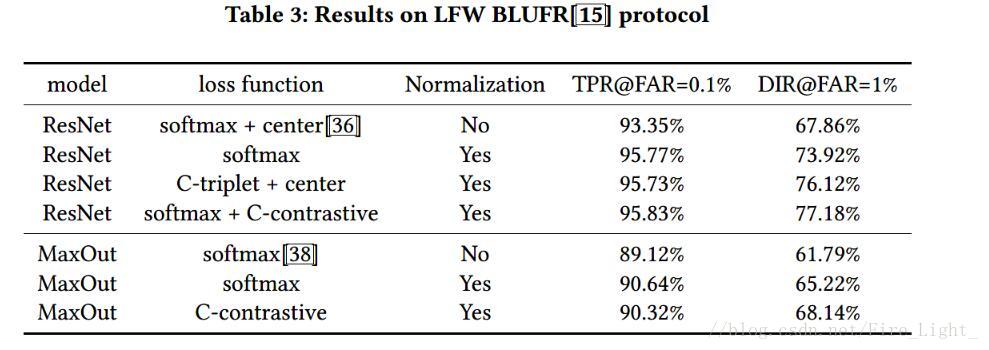
為了說明這個問題,作者特意做了試驗,說明進行人臉驗證時使用歸一化後的內積或者歐式距離效果明顯會優於直接計算兩個特徵向量的內積或者歐式距離,實驗的結果如下:
*注意這個Normalization不同於batch normalization,一個是對L2範數進行歸一化,一個是均值歸零,方差歸一。
那麼是否可以直接在訓練時也對特徵向量歸一化?
針對上面的問題,作者設計實驗,通過歸一化Softmax所有的特徵和權重來建立一個cosine layer,實驗結果是網路不收斂了。
本論文要解決的四大問題:
1.為什麼在測試時必須要歸一化?
2.為什麼直接優化餘弦相似度會導致網路不收斂?
3.怎麼樣使用softmaxloss優化餘弦相似度
4.既然softmax loss在優化餘弦相似度時不能收斂,那麼其他的損失函式可以收斂嗎?
L2歸一化
首先解釋問題1和2,即為什麼必須要歸一化和為什麼直接優化歸一化後的特徵網路不會收斂
為什麼要歸一化?
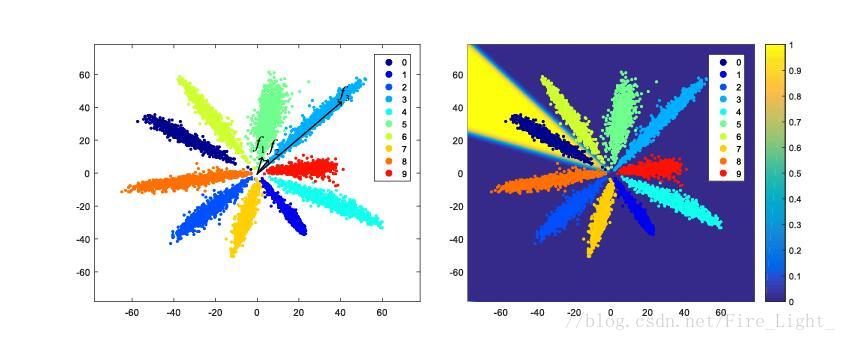
全連線層特徵降至二維的MNIST特徵圖,(具體細節可以參考我的部落格人臉識別系列(十二):Center Loss)
左圖中,f2f3是同一類的兩個特徵,但是可以看到f1和f2的距離明顯小於f2f3的距離,因此假如不對特徵進行歸一化再比較距離的話,可能就會誤判f1f2為同一類。
為什麼會是特徵會呈輻射狀分佈
Softmax實際上是一種(Soft)軟的max(最大化)操作,考慮Softmax的概率
假設是一個十個分類問題,那麼每個類都會對應一個權值向量,某個特徵f會被分為哪一類,取決f和哪一個權值向量的內積最大。
對於一個訓練好的網路,權值向量是固定的,因此f和W的內積只取決與f與W的夾角。
也就是說,靠近的向量會被歸為第一類,靠近的向量會歸為第二類,以此類推。網路在訓練過程中,為了使得各個分類更明顯,會讓各個權值向量W逐漸分散開,相互之間有一定的角度,而靠近某一權值向量的特徵就會被歸為相應的類別,因此特徵最終會呈輻射狀分佈。
如果添加了偏置結果會是怎麼樣的?
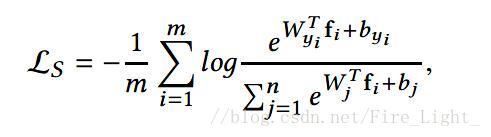
如果添加了偏置,不同類的b不同,則會造成有的類w角度近似相等,而依據b來區分的情況,如下圖。
在這種情況下如果再對w進行歸一化,那麼中間這些類會散步在單位圓上各個方向,造成錯誤分類。
所以新增偏置對我們通過餘弦距離來分類沒有幫助,弱化了網路的學習能力,所以我們不新增偏置。
網路為何不收斂
記得前面我們提到,作者做了實驗,通過歸一化Softmax所有的特徵和權重來建立一個cosine layer,實驗結果是網路不收斂了,接下來就解釋是為什麼。
歸一化後的內積
是一個[-1,1]區間的數,經過softmax函式之後,即使各個類別都被完全分開了(即f和其標籤對應類的權值向量的內積為1,而與其他類的權值向量內積都是-1),其輸出的概率也會是一個很小的數:
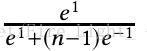
上式在n=10時,結果為0.45;在n=1000時,結果為 0.007,非常之小。
因此即使對於完全分開的類,由於梯度中有一項是(1-y),其梯度還是很大,因此無法收斂。
為了解決這一問題,作者提出了一個關於Softmax的命題來告訴大家答案。
命題:如果把所有的W和特徵的L2norm都歸一化後乘以一個縮放參數L,且假設每個類的樣本數量一樣,則Softmax損失
的下界(在所有類都完全分開的情況下)是
(文末貼出了證明過程)
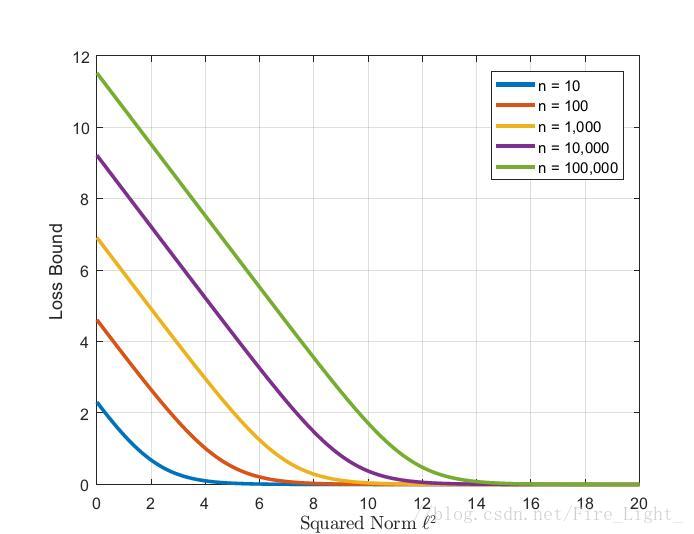
其下界和歸一化後縮放的引數l的函式圖大約如下:
因此,在歸一化層後新增一層放大層l可以解決無法收斂的問題。
歸一化層的定義
首先定義二範數,加一個很小的ε是為了防止歸一化時會除以0.
定義歸一化層
損失函式對歸一化層的求導如下(建議大家自行推導以加深印象):
根據上式可以推導,L對特徵x的梯度總是和x的特徵正交(文末貼出了證明過程),
因此經過梯度下降之後,x的範數總會增大,為了防止範數無限增大,需要使用權重衰減項。
改進度量學習
藉助於以上對Softmax的透徹研究,作者順手改進了一下度量學習通常要使用兩個損失函式contrastive loss與triplet loss。兩者原公式表達如下:
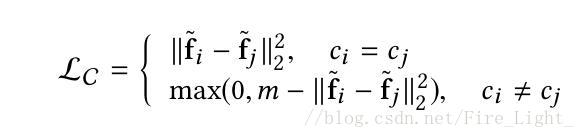
這兩者不同於Softmax的單項直接訓練,存在挖掘pairs/triplets耗費時間的問題。
藉助於Softmax直接以W與X相乘表示餘弦相似度的思路,改進以上兩種Loss為
Wj作為對應項的權值向量,可以由網路自己訓練獲得。
改進之後的損失函式稱為C-contrastive/triplet loss。
試驗
訓練
作者使用個一個淺層的網路和一個深層的網路進行試驗,在全連線層後面進行歸一化,然後計算W和X的內積(Softmax)或是歐式距離(C-contrastive/triplet loss),然後按照上面的損失函式計算損失和梯度
學習率1e-4、1e-3 衝量0.9
驗證演算法
一張圖片和它的水平翻轉圖把特徵對應的位置相加(一般是相接),然後PCA,計算餘弦相似度
結果
LFW
1.使用淺層網路
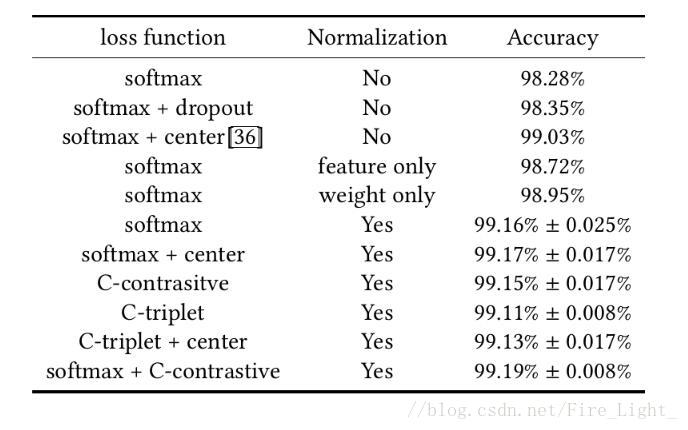
結果看上去Normalization比損失函式還重要
2.使用resnet
這個似乎是說明了resnet還是很有效的
附錄:命題的證明
證明一:
命題:如果把所有的W和特徵的L2norm都歸一化為L,且假設每個類的樣本數量一樣,則Softmax損失
的下界(在所有類都完全分開的情況下)是
證:
因為每個類樣本數量一樣,假設有n個類,則L等價於
(其中||Wi||=l,因為完全分開了,所以Wi可以代表該類特徵。)
同除得到
由於exp(x)的凸性,有
當且僅當Xi互相相等時等號成立
即
那麼
又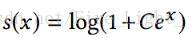
同是凸函式
有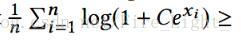
所以
注意到
所以
命題得證,考慮等號成立的條件需要任何WaWb內積相同,而對於h維向量W,只能找到h+1個點,使得兩兩連線的向量內積相同,如二維空間的三角形和三位空間的三面體,但是最終需要分類的數目可能遠大於特徵維度,所以經常無法取到下界。
證明二:
過程相對簡單
相關推薦
人臉識別系列(十四):NormFace
提出問題 之前的人臉識別工作,在特徵比較階段,通常使用的都是特徵的餘弦距離 而餘弦距離等價於L2歸一化後的內積,也等價L2歸一化後的歐式距離(歐式距離表示超球面上的弦長,兩個向量之間的夾角越大,弦長也越大) 然而,在實際上訓練的時候用的都是沒有L2
人臉識別系列(十七):ArcFace/Insight Face 人臉識別系列(十七):ArcFace/Insight Face
原 人臉識別系列(十七):ArcFace/Insight Face 2018年03月18日 18:00:31 Fire_Light_ 閱讀數:11370
人臉識別系列(十七):ArcFace/Insight Face
其實這篇論文可以看作是AmSoftmax的一種改進版本,總體思路相對較為簡單。 AmSoftmax: Arcface: 這樣修改的原因: 角度距離比餘弦距離在對角度的影響更加直接 決策邊界的具體比較如下圖 IR 除了
linux系列(十四):head命令
1、命令格式: head [引數] [檔案] 2、命令功能: head 用來顯示檔案的開頭至標準輸出中,預設head命令列印其相應檔案的開頭10行。 3、命令引數: -q 隱藏檔名 -v 顯示檔名 -c<位元組> 顯示位元組數 -n<行數&g
Docker系列(十四):Docker Swarm集群
mount dns 容器 water style 請求 兩種 ups task 一、Swarm簡介 Swarm是Docker官方提供的一款集群管理工具,其主要作用是把若幹臺Docker主機抽象為一個整體,並且通過一個入口統一管理這些Docker主機上的各種Docker資源。
人臉識別系列(十):Webface系列2
作者 CASIA 概述 為了得到更好的準確度,深度學習的方法都趨向更深的網路和多個模型ensemble,這樣導致模型很大,計算時間長。本文提出一種輕型的CNN,在取得比較好的效果同時,網路結構簡化,時間和空間都得到了優化,可以跑在嵌入式裝置和移動裝置
SpringBoot入門系列篇(十四):使用@Async註解進行非同步方法呼叫
非同步呼叫的概念 非同步呼叫相對於同步呼叫而言,通常的方法都是程式按照順序來執行的,程式的每一步都需要等到上一步執行完成之後才能繼續往下執行;而非同步呼叫則無需等待,它可以在不阻塞主執行緒的情況下執行高耗時方法 如何實現非同步呼叫 在不使用SpringBo
Android開發系列(十七):讀取assets文件夾下的數據庫文件
pack 取數 code ada tracking 編寫 數據庫 sdn where 在做Android應用的時候,不可避免要用到數據庫。可是當我們把應用的apk部署到真機上的時候,已經創建好的數據庫及其裏邊的數據是不能隨著apk一起安裝到真機上的。 (PS:這篇
Java框架spring Boot學習筆記(十四):log4j介紹
inf alt 技術分享 images 使用 image 詳細 配置文件 -128 功能 日誌功能,通過log4j可以看到程序運行過程的詳細信息。 使用 導入log4j的jar包 復制log4j的配置文件,復制到src下面 3.設置日誌級別
Android項目實戰(十四):TextView顯示html樣式的文字
sta ref RR per 使用 一個 title name Go 原文:Android項目實戰(十四):TextView顯示html樣式的文字項目需求: TextView顯示一段文字,格式為:白雪公主(姓名,字數不確定)向您發來了2(消息個數,不確定)條消息 這段文
Python筆記(十四):操作excel openpyxl模塊
align pre 一行 color value colspan xls str 工作 (一) 常遇到的情況 就我自己來說,常遇到的情況可能就下面幾種: 讀取excel整個sheet頁的數據。 讀取指定行、列的數據 往一個空白的excel文檔寫數據 往一
.NET面試題系列(十四)分布式鎖
情況 png 過期 www. tro 守護線程 自動 17. alt 如何解決分布式鎖超時問題 我們可以讓獲得鎖的線程開啟一個守護線程,用來給快要過期的鎖“續航” 當過去了29秒,線程A還沒執行完,這時候守護線程會執行expire指令,為這把
talib 中文文檔(十四):Math Transform Functions 數學變換
曲線 tor lib 函數 sin 中文 oot fun 函數名 Math Transform Functions ACOS - Vector Trigonometric ACos 函數名:ACOS 名稱:acos函數是反余弦函數,三角函數
java基礎學習總結(十四):Enum 型別的使用介紹
一、Enum 型別的介紹 列舉型別(Enumerated Type) 很早就出現在程式語言中,它被用來將一組類似的值包含到一種型別當中。而這種列舉型別的名稱則會被定義成獨一無二的型別描述符,在這一點上和常量的定義相似。不過相比較常量型別,列舉型別可以為宣告的變
PE檔案格式學習(十四):繫結匯入表
1.介紹 繫結匯入表的作用是加快程式的啟動速度,一個PE程式在啟動時會去載入匯入表中的dll檔案,並將匯入表的FirstThunk指向的陣列填入函式的真實地址,這需要耗去時間,繫結匯入表中儲存了匯入函式的真實地址,所以當PE在啟動時系統檢測到有繫結匯入表,就會直接將地址填入FirstThunk裡,這樣就省去
javaweb學習筆記(十四):JSP(4)
目錄 製作高仿的JSTL標籤庫之核心標籤庫 《1》xiaohua.tld檔案: 《2》依附的各個類: 《3》imitate.core.jsp檔案: 《4》瀏覽器檢視: 製作高仿的JSTL標籤庫之核心標籤庫 通過自定義標籤,製
大資料(十四):多job串聯與ReduceTask工作機制
一、多job串聯例項(倒索引排序) 1.需求 查詢每個單詞分別在每個檔案中出現的個數 預期第一次輸出(表示單詞分別在個個檔案中出現的次數) apple--a.txt 3 apple--b.txt 1 apple--c.txt 1 grape--a.txt
劍指offer系列(十四)二叉樹的深度,平衡二叉樹,陣列中只出現一次的數字
二叉樹的深度 題目描述 輸入一棵二叉樹,求該樹的深度。從根結點到葉結點依次經過的結點(含根、葉結點)形成樹的一條路徑,最長路徑的長度為樹的深度。 解題思路: 利用遞迴實現。如果一棵樹只有一個結點,那麼它的深度為1。遞迴的時候無需判斷左右子樹是否存在,因為如果該節點 為葉節點,它的左右
linux系列(十一):nl命令
調整 寫到 實例 空行 格式 指定格式 指定 所有 tab 1、命令格式: nl [選項] [文件] 2、命令功能: nl(Number of Lines) 將指定的文件添加行號標註後寫到標準輸出。如果不指定文件或指定文件為"-" ,程序將從標準輸入讀取數據。
Python之路(十四):網路程式設計基礎 Python基礎之網路程式設計
Python基礎之網路程式設計 學習網路程式設計之前,要對計算機底層的通訊實現機制要有一定的理解。 OSI 網際網路協議按照功能不同分為osi七層或tcp/ip五層或tcp/ip四層 可以將應用層,表示層,會