Opencv 3.4 的solvepnp中的P3P與EPnp位姿估計演算法解析
https://www.cnblogs.com/shang-slam/p/6481344.html
EPnP在ORB-SLAM中主要用於Tracking執行緒中的重定位Relocalization模組,需要通過當前關鍵幀Bow與候選幀匹配上的3D地圖點,迅速建立當前相機的初始姿態。
PnP問題解決了已知世界參考系下地圖點以及相機參考系下投影點位置時3D-2D相機位姿估計問題,不需要使用對極約束(存在初始化,純旋轉和尺度問題,且一般需要8對點),可以在較少的匹配點(最少3對點,P3P方法)中獲得較好的運動估計,是最重要的一種姿態估計方法。最後,如果知道世界參考系下的地圖點,同時知道相機參考系下的地圖點,可以通過ICP的方法去求解姿態。
這樣就構成了立體視覺中最重要的對極幾何,PnP和ICP三種最常用的姿態估計方法。
求解PnP問題目前主要有直接線性變換(DLT),P3P,EPnP,UPnP以及非線性優化方法。
DLT
直接構建一個12個未知數的[R|t]增廣矩陣(先不考慮旋轉矩陣的自由度只有3),取六個點對,去求解12個未知數(每一個3D點到歸一化平面的對映給出兩個約束),最後將[R|t]左側3*3矩陣塊進行QR分解,用一個旋轉矩陣去近似(將3*3矩陣空間投影到SE(3)流形上)。
P3P
P3P方法是通過3對3D/2D匹配點,求解出四種可能的姿態,在OpenCV calib3d模組中有實現,但是對於相機遠離3D平面(low parallax)或者視角垂直於3D平面的情況下效果不佳,不知道最近有沒有更新過。論文
將世界座標系下的ABC三點和影象座標系下的abc三點匹配,其中AB,BC,AC的長度已知,<a,b>,<b,c>,<a,c>也是已知,通過餘弦定理可以求出A,B,C在相機參考系中的座標,然後使用類似ICP的座標系對齊,就可以求得當前相機薇姿。
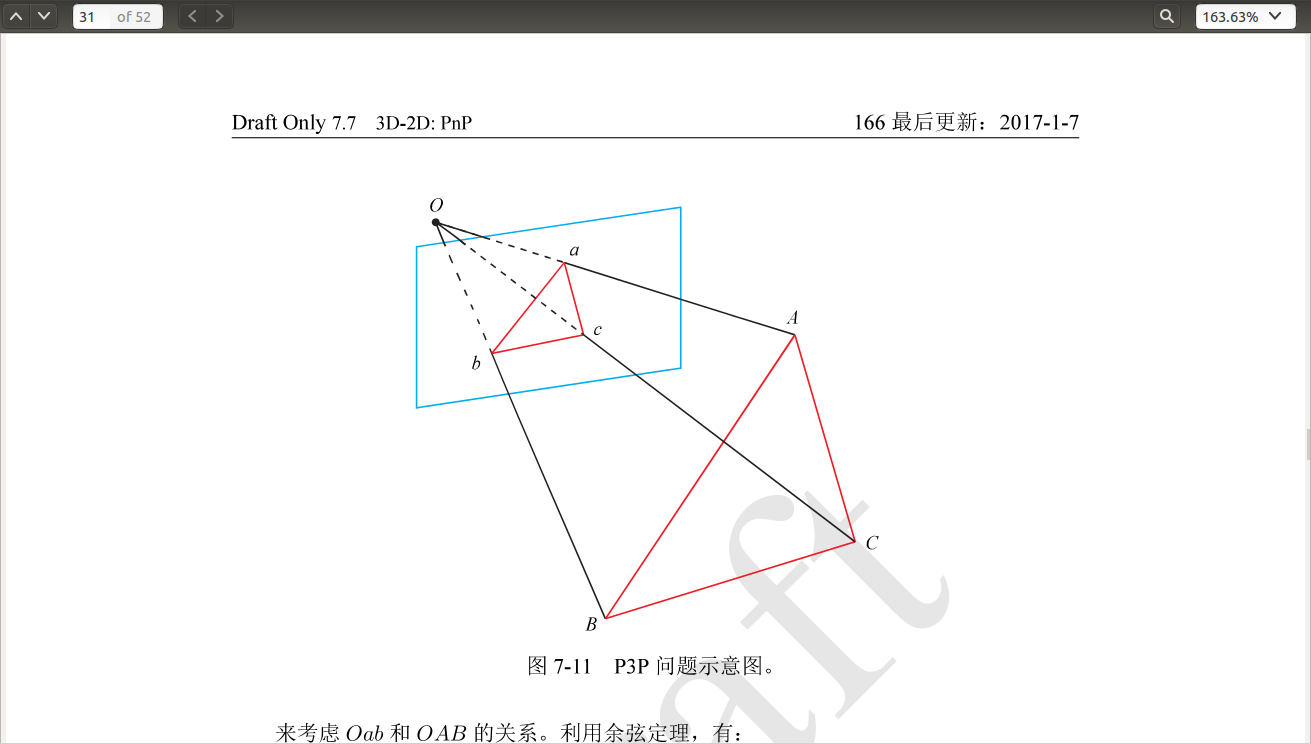
通過餘弦定理構建二元二次方程組【2】可以求解出OA,OB,OC之間的長度比例,從而確定世界座標系下的相機位姿。可以想象一下為什麼會出現四個解,在空間中的位置是什麼樣的,以及為什麼在遠離3D點平面或者視角垂直3D點平面時,會出現退化情況。
EPnP 需要4對不共面的(對於共面的情況只需要3對)3D-2D匹配點,是目前最有效的PnP求解方法。
The aim of the Perspective-n-Point problem—PnP in short—is to determine the position and orientation of a camera given its intrinsic parameters and a set of n correspondences between 3D points and their 2D projections. It has many applications in Computer Vision, Robotics, Augmented Re- ality and has receivedmuch attention in both the Photogrammetry and Computer Vision communities. In particular, applications such as feature point-based camera tracking require dealing with hundreds of noisy feature points in real-time, which requires computationally efficient methods.
空間中任意3D點的座標可以用4個不共面的3D點座標的權重表示
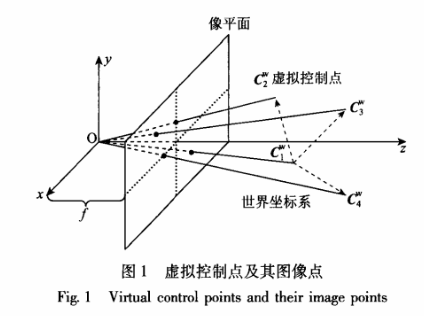
通常選取世界座標下的四個控制點座標為Cw=[0,0,0,1]T, [1,0,0,1]T,[0,1,0,1]T,[0,0,1,1]T;通過n個3D點在相機平面的投影關係,以及與這四個控制點的權重關係,構建一個12*12方陣,求得其零空間特徵向量,可以得到虛擬控制點的相機平面座標,然後使用POSIT演算法即可求出相機位姿。
通常在用EPnP求得四對點下的封閉解後,可以將該解作為非線性優化的初值,優化提高精度。
主要參考:
2. 高翔,視覺SLAM十四講
EPnP演算法
相機座標系用Fc
,世界座標系用Fw表示,任何一點可以用四個控制點pwi表示

對於相機座標系同樣成立

對於上面的公式,首先需要說明的是αij確實存在。因為cwj或ccj構成的方程組是欠定的,所以一定存在解。
理論上來說,控制點可以隨便選擇,這裡選擇控制點為參考點的中心,其他的點在PCA得到的主軸上單位長度處,從而提高演算法的穩定性。
控制點在相機座標系的座標
根據投影方程得到世界座標系中參考點座標和相機座標系中參考點的約束關係:

寫成矩陣的形式為:

將等式的第三列代入第一二列,得到
因此,可以得到下面的線性方程組:

上面的方程中,四個控制點總共12個未知變數,M為2n×12的矩陣。因此,x屬於M的右零空間,vi為矩陣M的右奇異向量,可以通過求解MTM的零空間特徵值得到。

[說明]使用MTM比使用M計算量更少,因為MTM是求解是常數複雜度,而M是O(n3)的複雜度,但是計算MTM的複雜度是O(n)
的。
選擇合適的線性組合
上面求解的x
中,需要確定βi,也就是確定合適的線性組合。根據參考點的位置不同,矩陣MTM的零空間維數可能為N=1→4維。求解β的策略是控制點在座標系w和c中,兩兩之間的距離是相同,而x的3k+1−3k分量表示分別表示不同的控制點在相機座標系中的座標,總共有C24=6個約束。
如果N=1,則根據約束有
其中L是由v1和v2構成的6×3的矩陣。
上面的方程可以通過β=(LTL)−1LTρ得到,然後通過選擇合適的符號從β21,β1β2,β22使得所有的pci有正的z座標。
如果N=3 則和N=2差不多,唯一的區別在於使用的是L的逆,而不是偽逆,此時的L為6×6的矩陣。
G-N優化
前面的步驟可以得到目標點在相機座標系中的閉式解,作為G-N優化的初始值,優化的變數為β=[β1,⋯,βN]T
,目標函式為

該優化過程和參考點的數目無關,優化步驟和時間是常數。
計算R,t
前面的兩步計算不同維數的零空間的誤差,選擇誤差最小維數對應的β
,從而得到x,恢復出控制點在相機座標系中的座標並根據質心座標系數得到參考點在相機座標系的座標。剩下的工作就是已知一組點雲在兩個座標系中的座標,求兩個座標系的位姿變換。
步驟如下:
(1)求中心點,pcc=∑picN,pcw=∑piwN;
(2)去中心,qic=pic−pcc,qiw=piw−pcw;
(3)計算H矩陣,H=∑Ni=1qicqiTw
(4)對H進行SVD,H=UΛVT;
(5)計算X=VUT,如果det(x)=1,則R=X,t=Pcc−RPcw。否則R(2,⋅)=−R(2,⋅)
這裡只介紹opencv3.4 中Epnp演算法的標頭檔案,具體內容可以參考論文《EPnP: An Accurate O(n) Solution to the PnP Problem》+opencv3.4 原始碼。
#ifndef epnp_h
#define epnp_h
#include "precomp.hpp"
#include "opencv2/core/core_c.h"
namespace cv
{
class epnp {
public:
/* max 註釋
* 函式功能:ePnP演算法的初始化建構函式,ePnP求解最少需要4對點,而且是相機內參已知
*
* 引數:
* [in] cameraMatrix 相機內參
* [in] opoints 參考點在世界座標系中的點,至少4個點-------float or double
* [in] ipoints 參考點在相機影象上的投影點座標,至少4個點-------float or double
* 返回值:
*
*/
epnp(const cv::Mat& cameraMatrix, const cv::Mat& opoints, const cv::Mat& ipoints);
~epnp();
// 此函式沒有實現---沒有使用
void add_correspondence(const double X, const double Y, const double Z,
const double u, const double v);
/* max 註釋
* 函式功能:ePnP演算法的初始化建構函式,ePnP求解最少需要4對點,而且是相機內參已知
*
* 引數:
* [out] R 旋轉矩陣3x3,世界座標系到相機座標系
* [out] t 平移向量,世界座標系到相機座標系
* 返回值:
*
*/
void compute_pose(cv::Mat& R, cv::Mat& t);
private:
epnp(const epnp &); // copy disabled
epnp& operator=(const epnp &); // assign disabled
// 初始化相機內參
template <typename T>
void init_camera_parameters(const cv::Mat& cameraMatrix)
{
uc = cameraMatrix.at<T> (0, 2);
vc = cameraMatrix.at<T> (1, 2);
fu = cameraMatrix.at<T> (0, 0);
fv = cameraMatrix.at<T> (1, 1);
}
// 將輸入的世界座標系的參考點和影象座標系中的點轉化到成員變數儲存
template <typename OpointType, typename IpointType>
void init_points(const cv::Mat& opoints, const cv::Mat& ipoints)
{
for(int i = 0; i < number_of_correspondences; i++)
{
pws[3 * i ] = opoints.at<OpointType>(i).x;
pws[3 * i + 1] = opoints.at<OpointType>(i).y;
pws[3 * i + 2] = opoints.at<OpointType>(i).z;
us[2 * i ] = ipoints.at<IpointType>(i).x*fu + uc;
us[2 * i + 1] = ipoints.at<IpointType>(i).y*fv + vc;
}
}
// 計算世界座標系的參考點在相機影象座標系下的投影誤差
double reprojection_error(const double R[3][3], const double t[3]);
// 選擇參考座標系中的控制點,第一個點為質心,第2-4個點PCA中的3個主成分方向上的點
void choose_control_points(void);
// 計算出論文中的alpha, 灰度質心齊次座標
void compute_barycentric_coordinates(void);
// 填充M矩陣,MX=0;
void fill_M(CvMat * M, const int row, const double * alphas, const double u, const double v);
// 根據計算的betas值和對應的特徵向量,計算相機座標系中的控制點
void compute_ccs(const double * betas, const double * ut);
// 通過相機座標系下的控制點,計算所有參考點在相機座標系下的座標;
void compute_pcs(void);
// 檢測參考點在相機座標系下的z軸座標是否大於零,大於零不做修改。如果小於零,需要按照相機光心(原點)中心對稱一下。
void solve_for_sign(void);
// 假設N=4,就是有4組特徵向量的組合來表示解
void find_betas_approx_1(const CvMat * L_6x10, const CvMat * Rho, double * betas);
// 假設N=2,就是有2組特徵向量的組合來表示解
void find_betas_approx_2(const CvMat * L_6x10, const CvMat * Rho, double * betas);
// 假設N=3,就是有3組特徵向量的組合來表示解
void find_betas_approx_3(const CvMat * L_6x10, const CvMat * Rho, double * betas);
void qr_solve(CvMat * A, CvMat * b, CvMat * X);
double dot(const double * v1, const double * v2);
double dist2(const double * p1, const double * p2);
// 求beta時的rho向量,L*beta=rho
void compute_rho(double * rho);
// 求beta時的L矩陣(就是論文中N=4時,由最小的四個奇異值所對應的右特徵向量所組成) l_6x10 為輸出的L矩陣
void compute_L_6x10(const double * ut, double * l_6x10);
// 高斯牛頓迭代求解,只迭代5次。
void gauss_newton(const CvMat * L_6x10, const CvMat * Rho, double current_betas[4]);
// 高斯牛頓中的梯度
void compute_A_and_b_gauss_newton(const double * l_6x10, const double * rho,
const double cb[4], CvMat * A, CvMat * b);
// 計算相機座標系和世界座標系之間的變換
double compute_R_and_t(const double * ut, const double * betas,
double R[3][3], double t[3]);
// horn 的絕對定向演算法
void estimate_R_and_t(double R[3][3], double t[3]);
void copy_R_and_t(const double R_dst[3][3], const double t_dst[3],
double R_src[3][3], double t_src[3]);
double uc, vc, fu, fv; // 相機內參
std::vector<double> pws, us, alphas, pcs; // pws 參考點在世界座標系中的座標; us 對應世界點在影象座標系上的投影; alphas 與論文中的一樣;pcs 參考點在相機座標系中的座標
int number_of_correspondences; // 對應點的個數
double cws[4][3], ccs[4][3]; //cws 參考座標系中4個3D參考點; ccs 相機座標系中4個3D 參考點
int max_nr;
double * A1, * A2; // 高斯牛頓使用的量
};
}
#endifOpencv 3.4 中P3P位姿估計演算法解析
先上圖,Opencv3.4中用兩種演算法實現P3P位姿估計問題。一種是基於距離P3P演算法問題(演算法1:P3P),一種是基於矩陣P3P演算法問題(演算法2:aP3P),具體推導細節可以參看論文還以整理的本地關鍵技術文件。此處只對程式進行分析註釋,方便以後使用。注意:此處只註釋演算法2,因為演算法1沒有完全搞明白(主要是高小山用wu-ritt演算法推導我看不太懂)。
外部呼叫介面函式:
/* max 註釋
* 函式功能:P3P位姿估計的介面函式,此函式可以利用不用的flags值,選擇不同的演算法。
* 輸入3個對應點,返回最多4組有效解
* 引數:
* [in] objectPoints 參考座標系(或世界座標系)中的3D點,需要3個即可,不要多也不要少。float和double都可以
* [in] imagePoints 對應3D點在相機相平面上的投影點的影象座標。需要3個即可,不要多也不要少。注意這個是2D的。float和double都可以
* [in] cameraMatrix 相機內參矩陣
* [in] distCoeffs 相機畸變矩陣
* [out] rvecs 輸出旋轉矩陣,不用宣告是多大矩陣-----輸出是最多是4個解----每個解的旋轉是用旋轉向量表示的。------從參考座標中的點到相機座標系的點的變換
* [out] tvecs 輸出平移矩陣,不用宣告多大矩陣------輸出最多是4個解。
* [in] flags 選擇不同的結算位姿演算法,SOLVEPNP_P3P是演算法1,採用基於距離PnP演算法。SOLVEPNP_AP3P演算法2,採用基於矩陣PnP演算法。
*
* 返回值:
* 返回解的個數,最大不會超過4個。
*/
int solveP3P(InputArray objectPoints, InputArray imagePoints, InputArray cameraMatrix, InputArray distCoeffs, OutputArrayOfArrays rvecs, OutputArrayOfArrays tvecs,int flags);測試例子:
#include "test_precomp.hpp"
void generate3DPointCloud(std::vector<cv::Point3f>& points, cv::Point3f pmin = cv::Point3f(-1, -1, 5), cv::Point3f pmax = cv::Point3f(1, 1, 10))
{
cv::RNG rng = cv::theRNG(); // fix the seed to use "fixed" input 3D points
for (size_t i = 0; i < points.size(); i++)
{
float _x = rng.uniform(pmin.x, pmax.x);
float _y = rng.uniform(pmin.y, pmax.y);
float _z = rng.uniform(pmin.z, pmax.z);
points[i] = cv::Point3f(_x, _y, _z);
}
}
void generateCameraMatrix(cv::Mat& cameraMatrix, cv::RNG& rng)
{
const double fcMinVal = 1e-3;
const double fcMaxVal = 100;
cameraMatrix.create(3, 3, CV_64FC1);
cameraMatrix.setTo(cv::Scalar(0));
cameraMatrix.at<double>(0, 0) = rng.uniform(fcMinVal, fcMaxVal);
cameraMatrix.at<double>(1, 1) = rng.uniform(fcMinVal, fcMaxVal);
cameraMatrix.at<double>(0, 2) = rng.uniform(fcMinVal, fcMaxVal);
cameraMatrix.at<double>(1, 2) = rng.uniform(fcMinVal, fcMaxVal);
cameraMatrix.at<double>(2, 2) = 1;
}
void generateDistCoeffs(cv::Mat& distCoeffs, cv::RNG& rng)
{
distCoeffs = cv::Mat::zeros(4, 1, CV_64FC1);
for (int i = 0; i < 3; i++)
distCoeffs.at<double>(i, 0) = rng.uniform(0.0, 1.0e-6);
}
void generatePose(cv::Mat& rvec, cv::Mat& tvec, cv::RNG& rng)
{
const double minVal = 1.0e-3;
const double maxVal = 1.0;
rvec.create(3, 1, CV_64FC1);
tvec.create(3, 1, CV_64FC1);
for (int i = 0; i < 3; i++)
{
rvec.at<double>(i, 0) = rng.uniform(minVal, maxVal);
tvec.at<double>(i, 0) = rng.uniform(minVal, maxVal / 10);
}
}
int main()
{
std::vector<cv::Point3f> points;
points.resize(500);
generate3DPointCloud(points);
std::vector<cv::Mat> rvecs, tvecs;
cv::Mat trueRvec, trueTvec;
cv::Mat intrinsics, distCoeffs;
generateCameraMatrix(intrinsics, cv::RNG());
generateDistCoeffs(distCoeffs, cv::RNG());
generatePose(trueRvec, trueTvec, cv::RNG());
std::vector<cv::Point3f> opoints;
opoints = std::vector<cv::Point3f>(points.begin(), points.begin() + 3);
std::vector<cv::Point2f> projectedPoints;
projectedPoints.resize(opoints.size());
projectPoints(cv::Mat(opoints), trueRvec, trueTvec, intrinsics, distCoeffs, projectedPoints);
std::cout << "intrinsics: " << intrinsics << std::endl;
std::cout << "distcoeffs: " << distCoeffs << std::endl;
std::cout << "trueRvec: " << trueRvec << std::endl;
std::cout << "trueTvec: " << trueTvec << std::endl;
std::cout << "oPoint: " << opoints << std::endl;
std::cout << "projectedPoints: " << projectedPoints << std::endl;
std::cout<<"result numbers A: :"<<solveP3P(opoints, projectedPoints, intrinsics, distCoeffs, rvecs, tvecs, cv::SOLVEPNP_AP3P)<<std::endl;
//std::cout << "result numbers: :" << solveP3P(opoints, projectedPoints, intrinsics, distCoeffs, rvecs, tvecs, cv::SOLVEPNP_P3P) << std::endl;
bool isTestSuccess = false;
double error = DBL_MAX;
for (unsigned int i = 0; i < rvecs.size() /*&& !isTestSuccess*/; ++i)
{
double rvecDiff = cvtest::norm(rvecs[i], trueRvec, cv::NORM_L2);
double tvecDiff = cvtest::norm(tvecs[i], trueTvec, cv::NORM_L2);
isTestSuccess = rvecDiff < 1.0e-4 && tvecDiff < 1.0e-4;
error = std::min(error, std::max(rvecDiff, tvecDiff));
std::cout << "i: " << i << std::endl;
std::cout << "error: " << error << std::endl;
std::cout << "rvec: " << rvecs[i] << std::endl;
}
system("pause");
}演算法2中程式碼描述,下面所描述的不是Opencv外部提供的介面,屬於演算法的內部實現。---程式碼在ap3p.h標頭檔案中。
#ifndef P3P_P3P_H
#define P3P_P3P_H
#include "precomp.hpp"
namespace cv {
class ap3p {
private:
template<typename T>
void init_camera_parameters(const cv::Mat &cameraMatrix) {
cx = cameraMatrix.at<T>(0, 2);
cy = cameraMatrix.at<T>(1, 2);
fx = cameraMatrix.at<T>(0, 0);
fy = cameraMatrix.at<T>(1, 1);
}
template<typename OpointType, typename IpointType>
void extract_points(const cv::Mat &opoints, const cv::Mat &ipoints, std::vector<double> &points) {
points.clear();
int npoints = std::max(opoints.checkVector(3, CV_32F), opoints.checkVector(3, CV_64F));
points.resize(5*npoints);
for (int i = 0; i < npoints; i++) {
points[i * 5] = ipoints.at<IpointType>(i).x * fx + cx;
points[i * 5 + 1] = ipoints.at<IpointType>(i).y * fy + cy;
points[i * 5 + 2] = opoints.at<OpointType>(i).x;
points[i * 5 + 3] = opoints.at<OpointType>(i).y;
points[i * 5 + 4] = opoints.at<OpointType>(i).z;
}
}
void init_inverse_parameters();
double fx, fy, cx, cy;
double inv_fx, inv_fy, cx_fx, cy_fy;
public:
// 3個初始化建構函式的目的是獲取相機內參數,並且計算相機內參矩陣的逆。---------用於求解論文中的bearing measurement
ap3p() : fx(0), fy(0), cx(0), cy(0), inv_fx(0), inv_fy(0), cx_fx(0), cy_fy(0) {}
ap3p(double fx, double fy, double cx, double cy);
ap3p(cv::Mat cameraMatrix);
/* max 註釋
* 函式功能:此處的位姿估計只返回一個解,並且此處輸入的是4個點---注意並不是solveP3P所呼叫。呼叫順序為①-->④-->③
* 引數:
* [out] R 輸出單個旋轉矩陣
* [out] tvec 輸出單個平移向量
* [in] opoints 輸入3D點---4個
* [in] ipoints 輸入2D點---4個
*
* 返回值:
* 成功返回true,失敗返回false
*/
① bool solve(cv::Mat &R, cv::Mat &tvec, const cv::Mat &opoints, const cv::Mat &ipoints);
/* max 註釋
* 函式功能:此處的位姿估計只返回最多4個解,是solveP3P所呼叫。呼叫順序為②-->③
* 引數:
* [out] R 輸出最多4個旋轉矩陣
* [out] tvec 輸出最多4平移向量
* [in] opoints 輸入3D點---3個
* [in] ipoints 輸入2D點---3個
*
* 返回值:
* 成功返回true,失敗返回false
*/
② int solve(std::vector<cv::Mat> &Rs, std::vector<cv::Mat> &tvecs, const cv::Mat &opoints, const cv::Mat &ipoints);
③ int solve(double R[4][3][3], double t[4][3],
double mu0, double mv0, double X0, double Y0, double Z0,
double mu1, double mv1, double X1, double Y1, double Z1,
double mu2, double mv2, double X2, double Y2, double Z2);
④ bool solve(double R[3][3], double t[3],
double mu0, double mv0, double X0, double Y0, double Z0,
double mu1, double mv1, double X1, double Y1, double Z1,
double mu2, double mv2, double X2, double Y2, double Z2,
double mu3, double mv3, double X3, double Y3, double Z3);
// 此處完全按照論文的計算步驟來的,程式非常清晰,可以參考論文
// This algorithm is from "Tong Ke, Stergios Roumeliotis, An Efficient Algebraic Solution to the Perspective-Three-Point Problem" (Accepted by CVPR 2017)
// See https://arxiv.org/pdf/1701.08237.pdf
// featureVectors: 3 bearing measurements (normalized) stored as column vectors
// worldPoints: Positions of the 3 feature points stored as column vectors
// solutionsR: 4 possible solutions of rotation matrix of the world w.r.t the camera frame
// solutionsT: 4 possible solutions of translation of the world origin w.r.t the camera frame
int computePoses(const double featureVectors[3][3], const double worldPoints[3][3], double solutionsR[4][3][3],
double solutionsT[4][3]);
};
}
#endif //P3P_P3P_H相關推薦
Opencv 3.4 的solvepnp中的P3P與EPnp位姿估計演算法解析
https://www.cnblogs.com/shang-slam/p/6481344.html EPnP在ORB-SLAM中主要用於Tracking執行緒中的重定位Relocalization模組,需要通過當前關鍵幀Bow與候選幀匹配上的3D地圖點,迅速建立當前相機的初
Visual Studio 2017 + OpenCV 3.4.1 全新安裝與配置及可能遇到的問題解決
系統環境:windows 10 + VS 2017 + OpenCV3.4.1 01 安裝 VS 2017 在微軟官網下載、安裝VS2017 Community(社群免費版)。 02 安裝 OpenCV 3.4.1 在OpenCV官網下載
相機位姿估計3:根據兩幅影象的位姿估計結果求某點的世界座標_0
關鍵詞:相機位姿估計,單目尺寸測量,環境探知 用途:基於相機的環境測量,SLAM,單目尺寸測量 文章型別:原理說明、Demo展示 @Author:VShawn @Date:2016-11-28 @Lab: [email protected] 目錄 《相機位姿估計
物體的三維識別與6D位姿估計:PPF系列論文介紹(三)
作者:仲夏夜之星 Date:2020-04-08 來源:物體的三維識別與6D位姿估計:PPF系列論文介紹(三) 文章“A Method for 6D Pose Estimation of Free-Form Rigid Objects Using Point Pair Features on Ran
Ubuntu16.04安裝OpenCV-3.4.3的C++和python版本(含anaconda建立的python環境)詳細步驟與總結(乾貨)
一、原始碼編譯安裝(C++版) 1.安裝一系列依賴項: sudo apt-get install build-essential sudo apt-get install cmake git libgtk2.0-dev pkg-config libavcodec-dev
(1)OpenCV-3.4.1+VS2017的安裝與配置
一、安裝VS20171、開啟微軟官網點選開啟連結在最下方點選Visual Studio 2017社群版進行下載(社群版註冊就可以免費使用,適用於學生和個人開發者);2、啟動下載的vs_Community.exe檔案,如果未安裝.NET Framework 4.6或更高版本,程
OPenCV筆記(3.4.1環境配置與擴充套件包編譯 vs 2017 和Qt 5.11)
1.官網 https://opencv.org/2.下載標準包 https://opencv.org/releases.html下載winpack之後解壓,配置環境變數,此方法只能使用標準的釋出庫,一些特別的庫無法使用,比如人臉識別的庫3.如果需要人臉識別等特殊的庫3.41版
OpenCV -Android Studio 中使用(opencv-3.4.0-android-sdk)
一、匯入程式 1. 確定SdkVersion 在匯入程式之前,我們需要先確定待會的OpenCv工程中的一些和SdkVersion有關的配置,最好的辦法就是先用AS建一個HelloWorld,也可以順便熟悉一下Android Studio的開發流程
Windows下VS2017編譯OpenCV 3.4.0-rc
打開 extra 地址 erl lap 頭文件 mas encode master 簡述 很久沒有用過OpenCV了,這次需要做一點圖像處理相關的工作,又需要用起來,這裏記錄一下編譯的過程。之前介紹過使用vs2015編譯opencv2.4的帖子在這裏。 編譯好的文件在這裏h
Ubuntu16.04下安裝opencv-3.4.1
百度 asp libjpeg ID 添加 dconf mkdir 文件目錄 fly 前期準備 下載OpenCV源碼包 進入OpenCV官方下載頁面```https://opencv.org/releases.html``` 選擇Sources類型 下載(這
opencv-3.4.2-android-sdk.zip國內下載鏡像
點擊下載 -s https mir 直接下載 http rar 復制粘貼 android-s 官網鏈接:https://opencv.org/releases.html鏈接:https://sourceforge.net/projects/opencvlibrary/ 。。
Ubuntu 16.04 安裝OpenCV 3.4.3
iba get 2.0 avcodec 依賴庫 4.3 build cmake efi 1.準備依賴庫 [編譯] sudo apt-get install build-essential [必需] sudo apt-get install cmake git libgtk
VS2017 + opencv 3.4.1 配置 簡記 (window 64位)
step1 下載opencv: 下載地址 下載完畢後點擊解壓得到 將 D:\cv1012\opencv\build\x64\vc15\bin 新增到環境變數 step2 下載VS2017:
opencv 3.4.3 + VS 2015 環境配置,親測有測試程式碼
今天要做一個實驗,需要用到opencv,所以打算寫一些程式碼,結果按照網上的配置都有一些問題。所以把自己正確配置的經驗給出來。 首先作者使用的是opencv-3.4.3-vc14_vc15.exe這個檔案,檔案的下載地址在 https://sourceforge.net/projects/o
【直搗黃龍】樹莓派安裝OpenCV 3.4.1
首先把準備工作做好,先確保已經更換好源:樹莓派換源 首先說說配置:我的樹莓派是2018年11月份買的,系統是2018-11-13-raspbian-stretch 附上:樹莓派系統下載地址 本文程式碼均可直接複製進shell 1.安裝OpenCV 依賴包: a. 更新軟體源
Windows下OpenCV 3.4.0 + Visual Studio 2015開發環境的配置
OpenCV3.1.0+VS2015開發環境配置 摘要: 由於最近AR(增強現實)這個概念非常火爆,各種基於AR的應用及遊戲逐漸面向大眾,而在AR中最重要的兩個技術就是跟蹤識別和增強渲
json.decoder.JSONDecodeError: Invalid control character at: line 1 column 3,python中str與json型別轉換報錯如何解
使用json轉: json資料保密,再此不展示。 # 判斷型別 print(type(str_json)) json_dump = json.loads(str_json) 報錯如下: json.decoder.JSONDecodeError: Invalid control cha
struts2[3.4]OGNL表示式語句與struts2框架的結合原理--引數賦值
1.三種方式:屬性驅動、物件驅動、模型驅動 2.測試 2.1模型驅動: 2.1.1(深入瞭解框架原理的操作方式)實現模型驅動只需在賦值前,將引數的物件壓入棧頂即可!所以,在未使用攔截器實現Prep
MATLAB-2016b+VS2017+OpenCV-3.4.1+mexopencv-3.3.1
使用mexopencv-3.3.1實現matlab與opencv混編 1.下載安裝MATLAB-2016b、VS2017、OpenCV-3.4.1、mexopencv-3.3.1。 2.下載並在matlab中新增msvc2017.xml和msvcpp2017.xml。
vs2017 +opencv 3.4.1 connected to each other
vs 與 opencv 的安裝不多說,百度一搜兩個軟體就可以官網獲取最新免費版本。 vs儘量不要安裝在C盤。 重點說以一下兩個軟體的適配: 首先,在安裝軟體時 ,不要急躁,否則,blabla~~~~ 步驟: (1) 更改環境變數 右擊 計算機 》》 屬性




