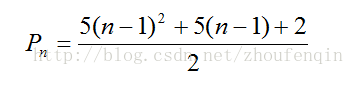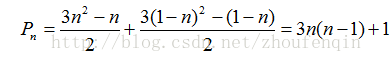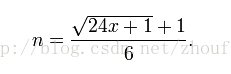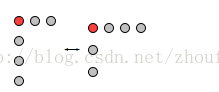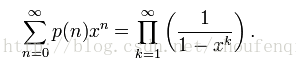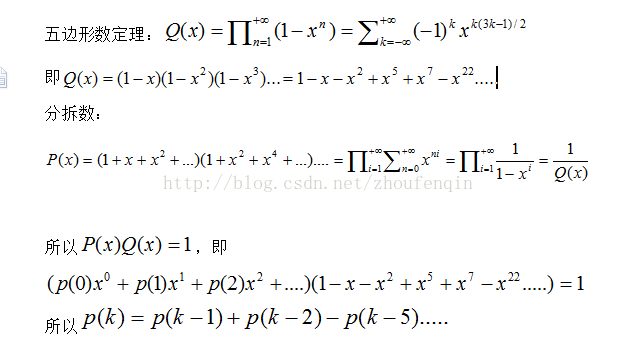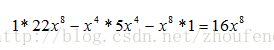分拆數 && hdu 4651 && hdu 4658
分拆數
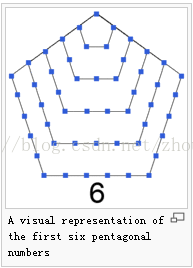
在將分拆數之前先介紹一點五邊形數
第n個五邊形數公式:p(n)=(3*n^2-n)/2
前幾個五邊形數:1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287, 330, 376, 425, 477, 532, 590, 651, 715, 782, 852, 925, 1001 .........
2. 廣義五邊形數:
n的取值0,1,-1,2,-2,3,-3.......
前幾個廣義五邊形數:0, 1, 2, 5, 7, 12, 15, 22, 26, 35, 40, 51, 57, 70, 77, 92, 100, 117, 126, 145, 155, 176, 187, 210, 222, 247, 260, 287, 301, 330......
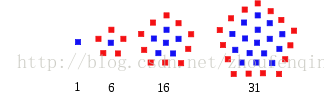
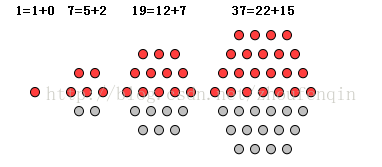
3. 中心五邊形數:
4.中心六邊形數
中心六邊形數跟廣義五邊形數有較大的關係,見圖
(相鄰兩個廣義五邊形數之和)
5. 五邊形數測試
利用以下的公式可以測試一個正整數x是否是五邊形數(此處不考慮廣義五邊形數):
若n是自然數,則x是五邊形數,而且恰為第n個五邊形數。
若n不是自然數,則x不是五邊形數。
進入正題:分拆數
將一個數用一個或多個正整數的無序和來表示
例如4的分拆有5種:4 , 3+1 , 2+2 , 2+1+1 , 1+1+1+1
1. 限制分拆
給一些分拆加限制條件。例如8的分拆有22種,
其中分拆的數中全部都是奇數的有6
同樣,若要求8分拆的數中是兩兩不同的也有6種:8, 7+1, 6+2, 5+3, 5+2+1, 4+3+1
一些有關限制分拆的結論:
·n的分拆數中最大部分為m的個數=把n分拆成m部分的個數
如圖,左邊最大部分m=3,等於把n拆成3部分(右圖) 把圖轉置即可
·n的分拆數中每一部分都小於等於m的個數=把n分成m份或更小
·n的分拆數中每部分的數都相等的個數=n 的因子個數
Eg. 6=2+2+2, 6=3+3,6=1+1+1+1+1+1
·n的分拆數中每部分都是
Eg. 6=1+1+1+1+1+1, 6=1+1+1+1+2, 6=1+1+2+2, 6=2+2+2
·n的分拆數中每部分都是1或2或3(或者把n分拆成1或2或3部分)的個數=(n+3)^2/12;
2. 生成函式
因為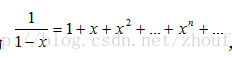
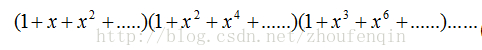
Pn 等於方程n=a1+2*a2+3*a3+...+n*an 的非負整數解a1,a2...an 的個數。
若是用母函式的方法去做,n很大不容易解出來,繼續往下看
定義P(k,n)為:將n表示成>=k 的數之和。Eg P(3,6): 6=3+3
1) 當最小的數為k時,p(k,n) = p(k,n-k)。即在n-k表示成>=k的數之和的情況下再加入一個k,情況還是不變
2) 當最小的數>k時,則至少最小的數為k+1,p(k,n)=p(k+1,n);
所以p(k,n)=p(k,n-k)+p(k+1,n)。k>n 時,p(k,n)=0,p(n,n)=1;

得到下表:
|
K n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
... |
|
1 |
1 |
|||||||
|
2 |
2 |
1 |
||||||
|
3 |
3 |
1 |
1 |
|||||
|
4 |
5 |
2 |
1 |
1 |
||||
|
5 |
7 |
2 |
1 |
1 |
1 |
|||
|
6 |
11 |
4 |
2 |
1 |
1 |
1 |
||
|
7 |
15 |
4 |
2 |
1 |
1 |
1 |
1 |
|
|
... |
前幾個分拆數1, 1, 2, 3, 5, 7, 11, 15, 22, 30, 42 ,56,77,101,135......
如果是按p(k,n)=p(k+1,n)+p(k,n-k) 來算,複雜度仍是0(n^2),往下看
右邊的分母是尤拉函式,可寫成
可以發現等式右邊x的指數為擴充套件五邊形數,可根據之前介紹的擴充套件五邊形公式算得p(n)=(3*n^2-n)/2,係數符號為(-1)^(m+1)
於是 p(k) = p(k − 1) + p(k − 2) − p(k − 5) − p(k − 7) + p(k − 12) + p(k − 15) − p(k − 22) − ...
Eg p(10)=p(9)+p(8)-p(5)-p(3)。複雜度降低了
/*
總結:
五邊形數:0, 1, 2, 5, 7, 12, 15, 22, 26, 35....
對應下標:0, 1, -1, 2, -2, 3, -3, 4, -4 , 5.....
所以 可以在O(N^1.5)的時間內求出p(1),p(2),...p(n)。
*/
Hdu 4658 要求拆分的數中每個數出現的次數不能大於等於k次,則
已經求得,現在看Q(x^k)會怎麼樣
例如,當n=8,k=4時
滿足指數為8的乘積之和為:
所以將8拆分的數中每個數的個數小於4的有16個,分別為
8,1+7,1+1+6,1+1+1+5,6+2,1+5+2,1+1+4+2,1+1+1+3+2,4+2+2,1+3+2+2,1+1+2+2+2,1+1+3+3,1+4+3,5+3,2+3+3,4+4
hdu 4651
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
using namespace std;
typedef __int64 LL;
const int maxn=100010;
const LL MOD=1000000007;
LL dp[maxn];
LL Five(LL x)
{
LL ans=3*x*x-x;
return ans/2;
}
void _init()
{
dp[0]=1;
for(int i=1;i<maxn;i++)
{
for(int j=1;;j++)
{
LL k=Five(j);//獲取五邊形數
if(k<=i)
{
if(j%2==0)//判斷奇偶從而判斷係數為正還是為負
dp[i]=(dp[i]-dp[i-k]);
else
dp[i]=(dp[i]+dp[i-k]);
if(dp[i]>=MOD) dp[i]%=MOD;
if(dp[i]<0) dp[i]+=MOD;
k=Five(-1*j);
if(k<=i)
{
if(j%2==0)
dp[i]=(dp[i]-dp[i-k]);
else
dp[i]=(dp[i]+dp[i-k]);
if(dp[i]>=MOD) dp[i]%=MOD;
if(dp[i]<0) dp[i]+=MOD;
}
else
break;
}
else
break;
}
}
}
int main()
{
_init();
int T,n;
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
printf("%I64d\n",dp[n]);
}
return 0;
}
hdu 4658
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
using namespace std;
typedef __int64 LL;
const int Maxn=100010;
const LL MOD=1000000007;
LL Q[Maxn],P[Maxn];
LL GetQ(LL x)
{
LL ans=(LL)x*x*3-x;
return (ans/2)%MOD;
}
void _init()
{
Q[0]=0;
for(int i=1;i<Maxn;i++)
{
if(i&1) Q[i]=GetQ(i/2+1);
else Q[i]=GetQ(i/2*(-1));
}
P[0]=P[1]=1;
for(int i=2;i<Maxn;i++)
{
for(int j=1;;j++)
{
if(Q[j]>i) break;
int t=j;
if(t&1) t=t/2+1;
else t=t/2;
if(t&1)
P[i]=(P[i]+P[i-Q[j]]);
else
P[i]=(P[i]-P[i-Q[j]]);
if(P[i]>=MOD) P[i]%=MOD;
if(P[i]<0) P[i]+=MOD;
}
}
}
void solved(LL n,LL k)
{
LL ans=0;
for(int i=0;;i++)
{
if(Q[i]*k>n) break;
int t=i;
if(t&1) t=t/2+1;
else t=t/2;
if(t&1) ans=(ans-P[n-Q[i]*k]);
else ans=(ans+P[n-Q[i]*k]);
if(ans>=MOD) ans%=MOD;
if(ans<0) ans+=MOD;
}
printf("%I64d\n",ans);
}
int main()
{
_init();
int T;
LL n,k;
scanf("%d",&T);
while(T--)
{
scanf("%I64d%I64d",&n,&k);
solved(n,k);
}
return 0;
}
相關推薦
分拆數 && hdu 4651 && hdu 4658
分拆數 在將分拆數之前先介紹一點五邊形數 1. 五邊形數是能排成五邊形的多邊形數。 第n個五邊形數公式:p(n)=(3*n^2-n)/2 前幾個五邊形數:1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 2
LOJ #6268. 分拆數
ima 技術分享 oot .com true png swa 發現 inline 可以先將問題建模為 : 物品大小為1~inf 且每件物品數量無限 的背包選體積為1~n的方案數。 顯然物品體積只有1~n有用,我們不妨把 體積1~sqrt(n) 的物
LOJ #6268 分拆數
不會五邊形數的菜雞的分塊亂搞 LOJ #6268 題意 求前$ n$個數的整數劃分方案數,$ n \leq 10^5$ $ Solution$ 考慮暴力$ DP$ $ f(x,y)$表示放了$ x$個物品總體積為$ y$的方案數 轉移分增加一個物品和將前面所有物品的體積均增加$ 1$兩種
C - 分拆素數和 (HDU - 2098)
pac 記錄 sqrt esp 整除 枚舉 math space clas - 題目大意 正如題目一樣,就是將一個正偶數拆分成素數(記錄拆分的素數個數就行,不用寫出是那些素數)。 - 解題思路 去枚舉每個數是否能被輸入的數字整除,如果能就不行
hdu 5044 Tree (樹鏈剖分+標記數組)
chan main while class #define AR spa def ble 鏈接:http://acm.hdu.edu.cn/showproblem.php?pid=5044 這道題是真的有毒,之前用樹鏈剖分+線段樹寫,tle了一萬發,瘋狂優化,最後放棄了,
hdu 5274 數鏈剖分 /dfs+數狀陣列
注意 第一:點權為0.。。。 第 2:杭電擴充套件啊。。。 #pragma comment(linker, "/STACK:1024000000,1024000000") #include <iostream> #include<stdio.h>
hdu 4651 Partition 五邊形數定理
/* 五邊形數定理,給以下連結,不再累述 http://zh.wikipedia.org/wiki/%E4%BA%94%E9%82%8A%E5%BD%A2%E6%95%B8%E5%AE%9A%E7%90%86 */ #include<cstdio> #incl
數塔問題-hdu-2084(dp)
題目連結:http://acm.hdu.edu.cn/showproblem.php?pid=2084 思路:要求從頂到底的最大值,可以反過來考慮,從底部向上。 只有下面一行的最大值確定,這一行的最大值才能確定。 #include<iostream> #include<cstdi
洛谷 1784 數獨(hdu 1426 Sudoku Killer)
洛谷1784 數獨: 首先題意是,給你一個9x9的未填滿的數獨(未填滿用0表示),要求你將這些0的位置上填上數字,以滿足數獨的特性。 解析: 其實這道題爆搜就行,畢竟只是9x9的數獨,直接從每個0的位置開始搜即可 上程式碼: #include <bits/
動態規劃題目--數塔(HDU)
因為之前沒有怎麼接觸過演算法,在賽碼網上刷題,碰上了動態規劃類的題目。正好藉此機會系統的學習一下。 在嗶哩嗶哩上看演算法視訊,裡面講解了一道HDU上的題目,下面貼下題目描述: ime Limit: 1000/1000 MS (Java/Others) Memory
動態規劃:數塔問題 hdu 2084 dp
帶備忘錄的自頂向下: #include<iostream> #include<cstring> using namespace std; int tower[101][101
卡特蘭數 相關問題 hdu 5184 Brackets
題解:當n為奇數的時候答案是0。 先判斷字串的前面是否符合括號匹配,即對於任何字首左括號個數>=右括號個數。 設左括號個數為a右括號個數為b, m=n/2,問題可以轉化為在平面中從座標(a,b)沿網格走到(m,m) 且不跨過x=y這一條直線的方法數。資料太大,普通DP
HDU 2112 HDU Today(STL MAP + Djistra)
stl eof dji int ble mes tin std n) 題目鏈接:HDU Today 立即集訓要開始,抓緊時間練練手,最短路的基礎題,第一次用STL的map 題目非常水,可是錯了N遍。手賤了。本題不優點理的就是把地名轉化為數字 #include
HDU Today HDU杭電2112【Dijkstra || SPFA】
esc 眼神 inpu mark 數據 auto 結束 性格 以及 http://acm.hdu.edu.cn/showproblem.php?pid=2112 Problem Description 經過錦囊相助,海東集團最終度過了危機,從此。HDU的發展就
hdu2098分拆素數和(讀題很重要!!!)
output sca namespace bmi i++ text put esc cnblogs 分拆素數和 題目鏈接:http://acm.hdu.edu.cn/showproblem.php?pid=2098 Time Limit: 1000/1000 MS (Jav
如何確定Kafka的分區數、key和consumer線程數
為什麽 打包 lower 匹配 到來 har mit 技術分享 每一個 轉自:http://www.tuicool.com/articles/Aj6fAj3 如何確定Kafka的分區數、key和consumer線程數 在Kafak中國社區的qq群中,這個問題被提及的
分頁數算法
color parseint ges col count code spa script clas JavaScript版 var pagecount = parseInt((options.total + options.pagesize - 1) / option
SpringMVC+Mybatis實現的Mysql分頁數據查詢
space round nbsp sub hid append app return utf 周末這天手癢,正好沒事幹,想著寫一個分頁的例子出來給大家分享一下。 這個案例分前端和後臺兩部分,前端使用面向對象的方式寫的,裏面用到了一些回調函數和事件代理,有興趣的朋友可
使用Spring-MongoDB連接全球分布數據庫Cosmos DB(1)
使用 子項目 增加 不同的 選擇 使用方式 客戶 port 接口 分布式系統一直都是非常復雜的,尤其是分布式數據庫系統,你如何保證數據的一致性?你如何保證其性能和延遲?你如何實現全球分布而不需要客戶做復雜的配置?在CAP的定理之下,如何設計並對分布式數據庫系統做取舍?Azu
spark分區數,task數目,core數,worker節點個數,excutor數量梳理
span 技術分享 註意 mat utf jpg input lin part 作者:王燚光鏈接:https://www.zhihu.com/question/33270495/answer/93424104來源:知乎著作權歸作者所有。商業轉載請聯系作者獲得授權,非商業轉載