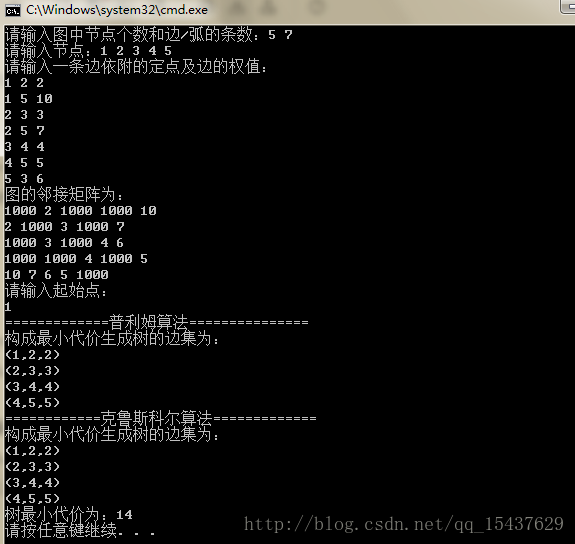
最小生成樹演算法：PRIM和 KRUSKAL

#include<stdio.h>
#include<stdlib.h>
#include<iostream>
#define MAX_VERTEX_NUM 20
#define OK 1
#define ERROR 0
#define MAX 1000
using namespace std;
typedef struct Arcell
{
    double adj;
}Arcell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
typedef struct
{
    char
 
 vexs[MAX_VERTEX_NUM]; //節點陣列
    AdjMatrix arcs; //鄰接矩陣
    int vexnum, arcnum; //圖的當前節點數和弧數
}MGraph;
typedef struct Pnode //用於普利姆演算法
{
    char adjvex; //節點
    double lowcost; //權值
}Pnode, Closedge[MAX_VERTEX_NUM]; //記錄頂點集U到V-U的代價最小的邊的輔助陣列定義
typedef struct Knode //用於演算法中儲存一條邊及其對應的2個節點
{
    char ch1; //節點1
    char
 
 ch2; //節點2
    double value;//權值
}Knode, Dgevalue[MAX_VERTEX_NUM];
//-----------------------------------------------------------------------------------
int CreateUDG(MGraph & G, Dgevalue & dgevalue);
int LocateVex(MGraph G, char ch);
int Minimum(MGraph G, Closedge closedge);
void MiniSpanTree_PRIM(MGraph G, char
 
 u);
void Sortdge(Dgevalue & dgevalue, MGraph G);
//-----------------------------------------------------------------------------------
int CreateUDG(MGraph & G, Dgevalue & dgevalue) //構造無向加權圖的鄰接矩陣
{
    int i, j, k;
    cout << "請輸入圖中節點個數和邊/弧的條數：";
    cin >> G.vexnum >> G.arcnum;
    cout << "請輸入節點：";
    for (i = 0; i<G.vexnum; ++i)
        cin >> G.vexs[i];
    for (i = 0; i<G.vexnum; ++i)//初始化陣列
    {
        for (j = 0; j<G.vexnum; ++j)
        {
            G.arcs[i][j].adj = MAX;
        }
    }
    cout << "請輸入一條邊依附的定點及邊的權值：" << endl;
    for (k = 0; k<G.arcnum; ++k)
    {
        cin >> dgevalue[k].ch1 >> dgevalue[k].ch2 >> dgevalue[k].value;
        i = LocateVex(G, dgevalue[k].ch1);
        j = LocateVex(G, dgevalue[k].ch2);
        G.arcs[i][j].adj = dgevalue[k].value;
        G.arcs[j][i].adj = G.arcs[i][j].adj;
    }
    return OK;
}
int LocateVex(MGraph G, char ch) //確定節點ch在圖G.vexs中的位置
{
    int a;
    for (int i = 0; i<G.vexnum; i++)
    {
        if (G.vexs[i] == ch)
            a = i;
    }
    return a;
}
//typedef struct Pnode //用於普利姆演算法
//{
//    char adjvex; //節點
//    double lowcost; //權值
//}Pnode,Closedge[MAX_VERTEX_NUM]; //記錄頂點集U到V-U的代價最小的邊的輔助陣列定義
void MiniSpanTree_PRIM(MGraph G, char u)//普利姆演算法求最小生成樹
{
    int i, j, k;
    Closedge closedge;
    k = LocateVex(G, u);
    for (j = 0; j<G.vexnum; j++)
    {
        if (j != k)
        {
            closedge[j].adjvex = u;
            closedge[j].lowcost = G.arcs[k][j].adj;
        }
    }
    closedge[k].lowcost = 0;
    for (i = 1; i<G.vexnum; i++)
    {
        k = Minimum(G, closedge);
        cout << "(" << closedge[k].adjvex << "," << G.vexs[k] << "," << closedge[k].lowcost << ")" << endl;
        closedge[k].lowcost = 0;
        for (j = 0; j<G.vexnum; ++j)
        {
            if (G.arcs[k][j].adj < closedge[j].lowcost)
            {
                closedge[j].adjvex = G.vexs[k];
                closedge[j].lowcost = G.arcs[k][j].adj;
            }
        }
    }
}
int Minimum(MGraph G, Closedge closedge) //求closedge中權值最小的邊，並返回其頂點在vexs中的位置
{
    int i, j;
    double k = 1000;
    for (i = 0; i<G.vexnum; i++)
    {
        if (closedge[i].lowcost != 0 && closedge[i].lowcost < k)
        {
            k = closedge[i].lowcost;
            j = i;
        }
    }
    return j;
}
int mini = 0;//樹最小代價
void MiniSpanTree_KRSL(MGraph G, Dgevalue & dgevalue)//克魯斯卡爾演算法求最小生成樹
{
    int p1, p2, i, j;
    int bj[MAX_VERTEX_NUM]; //標記陣列
    for (i = 0; i<G.vexnum; i++) //標記陣列初始化
        bj[i] = i;
    Sortdge(dgevalue, G);//將所有權值按從小到大排序
    for (i = 0; i<G.arcnum; i++)
    {
        p1 = bj[LocateVex(G, dgevalue[i].ch1)];
        p2 = bj[LocateVex(G, dgevalue[i].ch2)];
        if (p1 != p2)
        {
            cout << "(" << dgevalue[i].ch1 << "," << dgevalue[i].ch2 << "," << dgevalue[i].value << ")" << endl;
            mini += dgevalue[i].value;
            for (j = 0; j<G.vexnum; j++)
            {
                if (bj[j] == p2)
                    bj[j] = p1;
            }
        }
    }
}
void Sortdge(Dgevalue & dgevalue, MGraph G)//對dgevalue中各元素按權值按從小到大排序
{
    int i, j;
    double temp;
    char ch1, ch2;
    for (i = 0; i<G.arcnum; i++)
    {
        for (j = i; j<G.arcnum; j++)
        {
            if (dgevalue[i].value > dgevalue[j].value)
            {
                temp = dgevalue[i].value;
                dgevalue[i].value = dgevalue[j].value;
                dgevalue[j].value = temp;
                ch1 = dgevalue[i].ch1;
                dgevalue[i].ch1 = dgevalue[j].ch1;
                dgevalue[j].ch1 = ch1;
                ch2 = dgevalue[i].ch2;
                dgevalue[i].ch2 = dgevalue[j].ch2;
                dgevalue[j].ch2 = ch2;
            }
        }
    }
}
void main()
{
    int i, j;
    MGraph G;
    char u;
    Dgevalue dgevalue;
    CreateUDG(G, dgevalue);
    cout << "圖的鄰接矩陣為：" << endl;
    for (i = 0; i<G.vexnum; i++)
    {
        for (j = 0; j<G.vexnum; j++)
            cout << G.arcs[i][j].adj << " ";
        cout << endl;
    }
    cout << "請輸入起始點：\n";
    cin >> u;
    cout << "=============普利姆演算法===============\n";
    cout << "構成最小代價生成樹的邊集為：\n";
    MiniSpanTree_PRIM(G, u);
    cout << "============克魯斯科爾演算法=============\n";
    cout << "構成最小代價生成樹的邊集為：\n";
    MiniSpanTree_KRSL(G, dgevalue);
    printf("樹最小代價為：");
    printf("%d\n",mini);
}

樣例：

最短路徑樹演算法：Dijkstra

#include <iostream>
#include <climits>
using namespace std;

#define MAX_VERTEX_NUM 20  // 頂點數量上限 
typedef char VerType;      // 頂點結構 , 頂點的字母名稱 
typedef int ArcType;       // 邊的結構 , 權值 
typedef enum { DG, UDG } GKind;  // 圖型別，{有向圖,無向圖}

                                 // 圖的儲存結構 
typedef struct
{
    int verNum, arcNum;  // 頂點數量, 邊數量 
    GKind kind;          // 圖型別 
    VerType vertex[MAX_VERTEX_NUM];                 //頂點
    ArcType arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM];   //邊 
}Graph;


void CreateGraphByArray(Graph &G);                 // 建立圖G (通過預定義的陣列)
int  VertexLoc(const Graph &G, const VerType &v);  // 獲取頂點v在圖G中的位置 
void ShortestPath_Dijkstra(Graph &G, int k);       // 最短路徑演算法 (迪傑斯特拉演算法)


int main()
{
    Graph G;
    CreateGraphByArray(G);
    ShortestPath_Dijkstra(G, 0);
    return 0;
}


void CreateGraphByArray(Graph &G)
{
    G.kind = DG;

    const int vn = 5;
    VerType V[vn + 1] = { "12345" };

    const int en = 7;
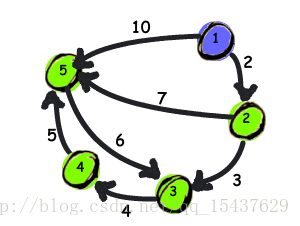
    VerType V1[en + 1] = { "1122345" };  //表示點1到2的距離為2；1到5的距離為10···
    VerType V2[en + 1] = { "2535456" };
    ArcType E[en] = { 2,10,3,7,4,5,6};


    // 輸入頂點 
    G.verNum = vn;
    for (int i = 0; i < G.verNum; ++i) {
        G.vertex[i] = V[i];
    }

    // 初始化鄰接矩陣 
    for (int vi = 0; vi < G.verNum; ++vi) {
        for (int vj = 0; vj < G.verNum; ++vj) {
            G.arcs[vi][vj] = INT_MAX;
        }
    }

    // 輸入邊 
    G.arcNum = en;
    for (int i = 0; i < G.arcNum; ++i) {
        VerType &v1 = V1[i], &v2 = V2[i];
        ArcType &e = E[i];
        int vi = VertexLoc(G, v1), vj = VertexLoc(G, v2);
        if (vi == G.verNum || vj == G.verNum) {
            continue;
        }
        if (UDG == G.kind) {
            G.arcs[vi][vj] = G.arcs[vj][vi] = e;
        }
        else {
            G.arcs[vi][vj] = e;
        }
    }
}

int VertexLoc(const Graph &G, const VerType &v)
{
    for (int i = 0; i < G.verNum; ++i) {
        if (G.vertex[i] == v) {
            return i;
        }
    }
    return G.verNum;
}

void ShortestPath_Dijkstra(Graph &G, int v0)
{
    const int N = 5;    //此處設定頂點個數********************************
    bool S[N];          // 表示v0到vi的最短路徑是否已經確定 
    int Path[N];        // 表示v0到vi的最短路徑上的直接前驅頂點 
    long long D[N];     // 表示v0到vi的最短路徑長度 

    for (int v = 0; v < N; ++v) {
        S[v] = false;
        D[v] = G.arcs[v0][v];
        Path[v] = D[v] != INT_MAX ? v0 : -1;
    }
    S[v0] = true;
    D[v0] = 0;

    for (int i = 1; i < N; ++i) {
        int min = INT_MAX, v;
        for (int w = 0; w < N; ++w) {
            if (!S[w] && D[w] < min) {
                v = w;
                min = D[w];
            }
        }

        if (min != INT_MAX) {
            S[v] = true;
            for (int w = 0; w < N; ++w) {
                if (!S[w] && (D[v] + G.arcs[v][w] < D[w])) {
                    D[w] = D[v] + G.arcs[v][w];
                    Path[w] = v;
                }
            }
        }
    }

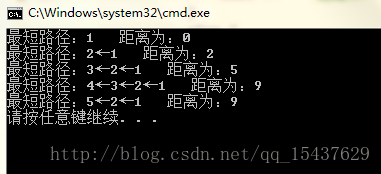
    /* 輸出最短路徑 */
    for (int vi = 0; vi < N; ++vi) {
        cout << "最短路徑：";

        cout << G.vertex[vi];
        if (S[vi]) {


            for (int vj = Path[vi]; vj != -1; vj = Path[vj]) {
                cout << "←" << G.vertex[vj];
            }


            cout << "   距離為：" << D[vi]  << endl;
        }
        else {
            cout << " (INF)" << endl;
        }
    }
}

結果：