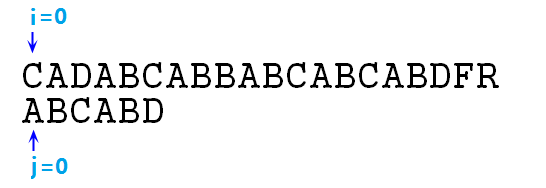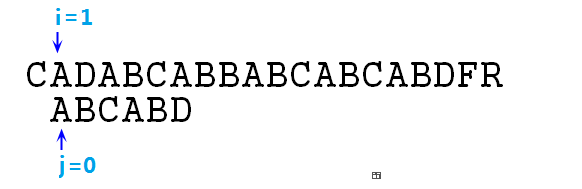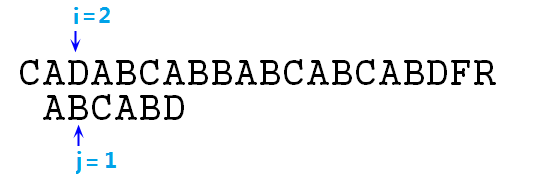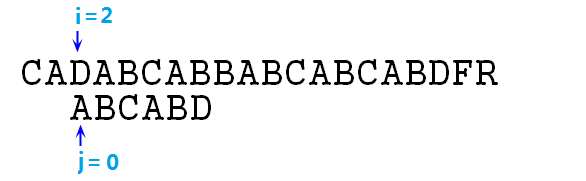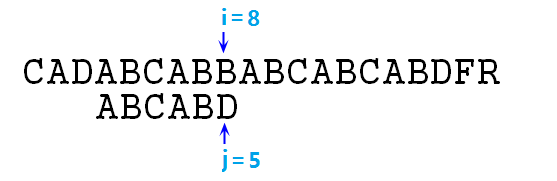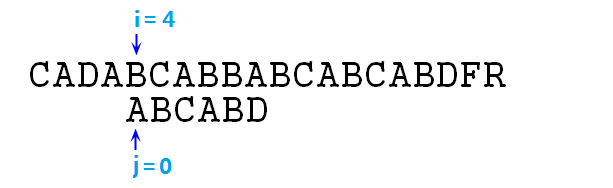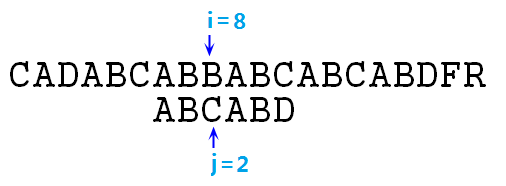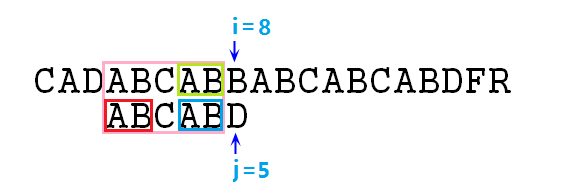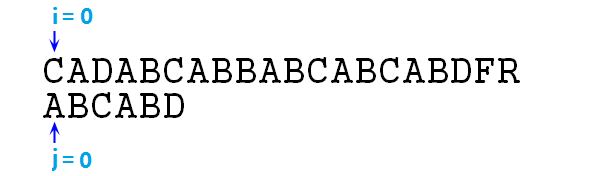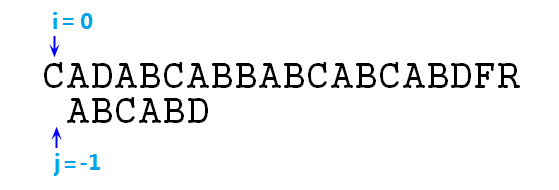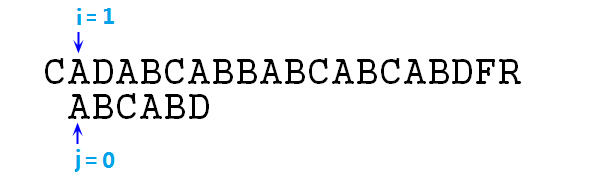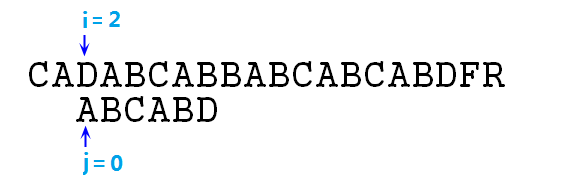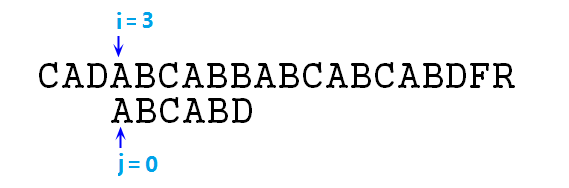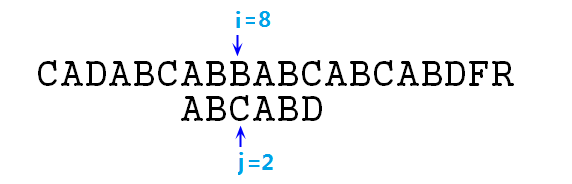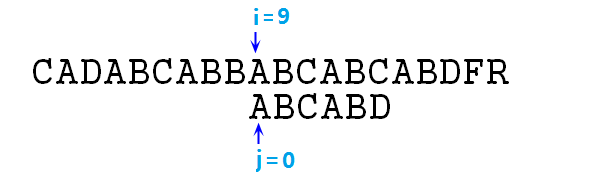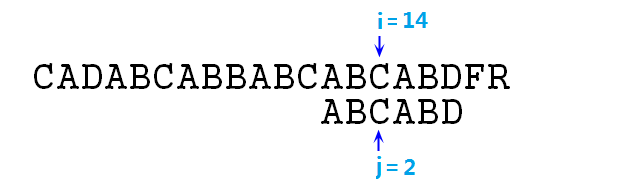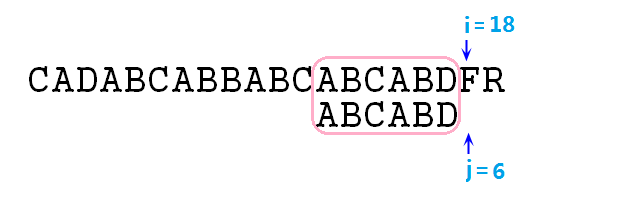本章是線性表的最後一部分——串。其實串就是我們日常所說的字串，它是一系列結點組成的一個線性表，每一個結點儲存一個字元。我們知道C語言裡並沒有字串這種資料型別，而是利用字元陣列加以特殊處理（末尾加'\0'）來表示一個字串，事實上資料結構裡的串就是一個儲存了字元的連結串列，並且封裝實現了各種字串的常用操作。

　　串的概念和定義其實沒什麼好說的，本章的主要內容是KMP演算法，也就是字串模式匹配演算法，本章後面會介紹到，我們下面所有提到的字串均使用順序結構，也就是字元陣列。我們先來介紹字串的一些常見的基本操作及實現。

串的常用操作

　　字串的常用操作大部分都已經被C/C++的標準庫實現了，我們下面直接介紹這幾個C函式

1.字串操作類

strcpy (s1, s2)

　　複製字串，將s2的內容複製到s1，函式原型_CRTIMP char* __cdecl __MINGW_NOTHROW strcpy (char*, const char*)，可以看出第二引數可以是常量也可以是變數，但第一引數必須是變數。這裡要注意的是s2的內容長度（包括'\0'）不能超出s1的總長度。該函式通常可以用來為字元陣列賦值，示例（第3行可以認為是在給cpy賦值）：

char str[233];
char cpy[233];
strcpy(cpy, "i am string");
strcpy(str, cpy);

strncpy(p, p1, n) 

　　複製指定長度字串，與上一個函式類似，只不過多了第三個引數，指的是要拷貝的字串的長度，此函式會將p1首地址開始的n個位元組的內容拷貝到p中，需要注意的是，拷貝後的內容並不包含字串結束標誌'\0'，所以需要手動新增才可使p變成需要的字串，示例：

char str[233];
char cpy[233] = "i am string";
strncpy(str, cpy, 8);
str[8] = '\0';

strcat(p, p1) 

　　字串連線 ，該函式會將p1的內容新增到p的末尾，比如p="Hello"，p1="World"，則執行該函式，p的內容變為"HelloWorld"。原型_CRTIMP char* __cdecl __MINGW_NOTHROW strcat (char*, const char*);

同樣第二引數可為常量，這裡需要注意的是，p和p1必須都是合法字串（即包含結束標誌'\0'）且需要保證連線後的總長度不會超過p的總大小。示例：

char str[233] = "Hello";
char cat[233] = "World";
strcat(str, cat);

strncat(p, p1, n) 

　　附加指定長度字串，類似上面strcpy和strncpy的區別，這裡也是一樣的，擷取p1前n個位元組的內容新增到p的末尾，注意，此函式會覆蓋p末尾的'\0'，並在新增p1完成後自動在最後新增'\0'，所以無需像上面那樣手動加'\0'。示例：

char str[233] = "Hello";
char cat[233] = "Worldxxx";
strncat(str, cat, 5);

strlen(p) 

　　取字串長度，這是我們最常用的一個函數了，得到字串長度，沒什麼好說的，需要注意的是p必須為合法字串，即有'\0'，下文中若再次提到“合法字串”即為“包含“'\0'”的字串 。還有一點是，該函式返回值為字串的字元數，要區別於字串佔用空間，比如對於字串"love"，它的長度為4，而佔用空間為5，strlen對於此字串的返回值即為4，示例：

char str[233] = "Hello";
int len = strlen(str);

strcmp(p, p1) 

　　比較字串，即比較p與p1的字典序大小，如果p比p1小（p字典序靠前），則返回-1；若p比p1大（p字典序靠後），則返回1；若兩字串一樣，則返回0。所謂的字典序，指的是將字串首部對齊，從左到右依次比較對應位置的字元大小，直至找到第一個不一樣的位置，其大小關係就是整個字串的大小關係（如果大寫與小寫比較，則實際是比較其ASCII碼），當然，如果比較到一個字串結束還未有結果，則短的字串靠前（想一下英文詞典裡單詞的排序）。

例如"a"<"b"，"food"<"foot"，"hack">"back"，"hasak">"hasa","bbc">"abcd"，"Ask"<"ask"等……

該函式通常用於判斷兩字串是否相等，兩引數均可為常量，示例（該例子res值為-1）：

char str[233] = "hello";
char cmp[233] = "world";
int res = strcmp(str, cmp);

strcasecmp(p, p1)

　　忽略大小寫比較字串，與上一個函式是同樣的功能，只不是上面是區別大小寫的，這裡是忽略大小寫，也就是說，此函式認為'a'和'A'是相等的，也就是說字串"abCdEFGhiJ"和"AbCDEfgHij"是相等的，返回值為0，示例（此例res為0）

char str[233] = "HEllo";
char cmp[233] = "hELlo";
int res = strcasecmp(str, cmp);

strchr(p, c) 

　　在字串中查詢指定字元， 即在p中從左向右查詢第一次出現字元c的位置（找不到就返回NULL），引數c可為字元或表示ASCII碼的整型。需要注意的是該函式的返回值並非下標整數值，而是一個代表該位置的地址，所以我們需要減去p的首地址即可得到該字元第一次出現的下標值。示例（下例res值為4）：

char str[233] = "Hello world";
char ch = 'o';
int res = strchr(str, ch) - str;

strrchr(p, c) 

　　在字串中反向查詢指定字元， 與上一個函式功能一致，只不過這個是從右向左查詢第一次出現的位置（返回值也是該位置的地址，找不到則NULL），同樣需要減去首地址來獲取索引下標值，示例（該res值為7）：

char str[233] = "Hello world";
char ch = 'o';
int res = strrchr(str, ch) - str;

strstr(p, p1) 

　　查詢字串， 上述兩個函式均是在字串裡查詢字元，這個函式是從字串查詢字串，也就是查詢字串的子串（找不到就返回NULL），在p中從左向右查詢第一次匹配了p1的位置，比如p為"abcdabcd"，p1為"bcd"，則執行函式，返回值為第一次匹配的地方即藍色的bcd中的b，同樣是返回地址，需要減去首地址得到下標，示例（此res為2）：

char str[233] = "Hello hello";
int res = strstr(str, "llo") - str;

　　此函式的效率不高，如果p和p1足夠長，那麼就會造成執行時間過慢，我們本章的KMP演算法就是處理此類字串匹配問題的高效演算法。

字串與數的轉換

atoi(p)

　　字串轉換到int型，該函式返回值為int，為p轉換成int後的值，不過p必須要合法，例如字串"123"可以轉換成整數123，但是字串"abc"不可以轉換。示例：

int res = atoi("666");

atof(p)

　　字串轉換到double型，與上面同理，轉換成double型且必須合法。 示例：

double res = atof("123.45");

atol(p) 

　　字串轉換到long整型，示例： 

long res = atol("666");

atoll(p)

　　字串轉換成long long型別，long  long即64位整型，示例：

long long res = atoll("666666666666666");

　　下面就是本章的重點內容：KMP演算法

字串模式匹配KMP演算法

　　***注意，下面的內容稍微有點難度，請注意仔細理解，切不可走馬觀花式的閱讀。

前言

　　KMP演算法是一種改進的字串匹配演算法，由D.E.Knuth，J.H.Morris和V.R.Pratt同時發現，因此人們稱它為克努特——莫里斯——普拉特操作（簡稱KMP演算法）。KMP演算法的關鍵是利用匹配失敗後的資訊，儘量減少模式串與主串的匹配次數以達到快速匹配的目的。具體實現就是實現一個next()函式，函式本身包含了模式串的區域性匹配資訊。時間複雜度O(m+n)。

字串暴力匹配

　　我們引入問題：假設有一個字串s，一個字串p，我們要找到p在s中第一次出現的位置，那麼應該如何尋找呢？我們第一反應應該是本文上半部分講到的字串操作函式strstr(s, p)來尋找字串位置，那麼我們不依賴已經實現好的函式，自己來實現解決應該如何處理呢？

　　首先想到的，就是將兩字串首端對齊，依次比較對應位置的字元，如果比對成功，則繼續比較下一個字元；如果失敗，那麼就要把p字串整體後移一個位置，重新開始比對對應位置的字元，直至p的所有字元都與s某段一一對應，匹配成功結束；否則匹配失敗。

　　我們圖解一個字串匹配問題，假設有字串s="CADABCABBABCABCABDFR"，p="ABCABD"，我們要尋找p在s中的位置，步驟分解如下 ：

　　① 首先我們使用指標i與指標j分別作s與p的下標，先使得i=j=0，即將s[0]與p[0]對齊，並且比較s[i]與p[j]，比對是否匹配，如圖：

　　② 顯然如上圖，s[i]與p[j]不匹配，所以我們需要將p字串整體右移一位，即i=1，j=0，如下圖所示：

　　③ 此時s[i]與p[j]匹配，所以繼續向下比較，即i和j同時右移，i=2，j=1，如下圖所示：

　　④ 顯然，此時s[i]與p[j]不匹配了，所以p字串整體右移，並重新開始匹配，即i=2，j=0，如下圖：

　　⑤ 此時不匹配，那麼繼續整體右移p字串，如下圖：

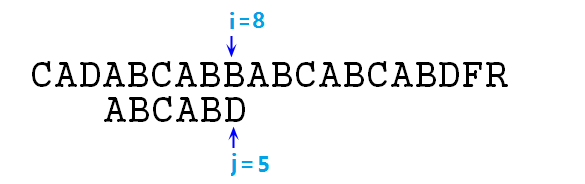
　　⑥ 此時s[i]=p[j]=A，可以繼續匹配，i++，j++，s[i]=p[j]=B……直至i=8，j=5時，失去匹配，如下圖：

　　⑦ 按照暴力匹配的思想，此時應該右移p字串，即令i=4，j=0，重新開始匹配。我們可以發現i指標發生了回溯，且回溯了4個字元的位置！回溯重置後如下圖：

　　⑧ 顯然，此時的s[i]與p[j]必然失配，由於我們在上一次匹配中（即p[0]與s[3]對齊時），我們已經知道了p[0]=A，p[1]=s[4]=B，所以對於此時i=4，j=0來說，s[i]=p[j]是絕對不成立的，所以i指標回溯回來也沒啥用，必然會失去匹配，i依然還要再次後移，浪費時間。那麼我們就需要一種演算法，使得在失去匹配時，i指標保持不動，直接移動j指標到相應位置即可，比如在第⑥步操作中，失去匹配後，i指標不動，直接將j指標置為2，如下圖：

　　⑨ 這樣，我們沒有使i指標回溯，而是直接將p字串移動了若干位，且保證了此時j指標前面的所有位置均匹配（s[6]=p[0]=A，s[7]=p[1]=B），我們現在只需要從現在的指標位置開始比較即可。這種跳躍式的匹配方式就是我們接下來要講的KMP演算法，此演算法分析利用了p字串的特點，保證了i指標的單向性，僅通過修改j的位置，即可使p串達到最合適的位置。

　　下面給出暴力匹配的程式碼：

int str_match(char *s, char *p) // 查詢p在s中的位置
{
    int i = 0;
    int j = 0;
    while(s[i] && p[j])
    {
        if(s[i] == p[j]) // 匹配，繼續執行
        {
            i++;
            j++;
        }
        else // 失去匹配，p後移
        {
            i = i - j + 1; // i-j代表此次匹配i的初始位置，再+1表示p後移
            j = 0;
        }
    }
    int len = strlen(p);
    if(j == len) // j與len相等，說明p字串匹配到結尾，即全部匹配成功
        return i - j; // 返回第一個匹配的位置
    return -1; // 無匹配，返回-1
}

模式匹配KMP演算法

　　在學習KMP演算法之前，我們先需要準備大量的前置知識，篇幅很長，請耐心閱讀學習。

字串字首字尾

　　何為字首字尾？簡單來說，將一個字串在任意位置分開，得到的左邊部分即為字首，右邊部分即為字尾。例如對於字串"abcd"，它的字首有"a"，"ab"，"abc"；字尾有"d"，"cd"，"bcd"。注意前後綴均不包括字串本身。

最長公共前後綴

　　對於一個字串來說，它既有字首，又有後綴，所謂的最長公共前後綴，即該字串最長的相等的字首和字尾。例如上面的字串"abcd"就沒有公共前後綴，更別提最長了，因為它的前後綴裡就沒有相等的；而字串"abcab"就有一個最長的公共前後綴即"ab"。

next陣列

　　那麼求最長公共前後綴到底有什麼用呢？我們先來分析暴力解法中第⑥步的操作，我把圖改了一下，請看圖：

　　如圖所示，當我們發現s[8]與p[5]失配的時候，暴力解法是令i=i-j+1，j=0，即p串右移一位。但更好的做法是保持i不變，j變為2，即讓s[8]與j[2]對齊，也就是p右移3位。那麼我們如何得到這個3位呢？也就是說，我們是怎麼知道j要指向2呢？這就要用到我們的公共前後綴了。

　　注意上圖，在此時失配，說明粉色框起來的部分是完全匹配的，那麼綠色框與藍色框匹配，而藍色部分是p字串粉色部分的字尾，紅色部分為p字串粉色部分的字首，恰好這個紅色部分與藍色部分相等，也就是說，p的粉色部分，也就是當前匹配成功的部分，有相等的前後綴。既然藍色匹配綠色 ，藍色等於紅色，那麼紅色必然匹配綠色，也就是說，我們只需將紅色部分與綠色部分對齊，j指標指向紅色部分的後一位，即可不更改i指標而繼續匹配下去。而我們的j指標要移動到的位置2，恰好是這個公共前後綴的長度2，所以，我們得出以下結論：

　　當s[i]與p[j]失配時，計算不包括p[j]在內的左邊子串（即p[0]~p[j-1]）的最長公共前後綴的長度，假設長度為k，則j指標需要重置為k，i不變，繼續匹配。

　　那麼現在的問題就是求最長公共前後綴了，總不能每次失配都要求一次子串的最長公共前後綴吧？而且好像這個最長公共前後綴只與p有關呢。所以，我們引入了next陣列，當p串在位置j失配的時候，需要將j指標重置為next[j]，而next[j]就代表了p字串的子串p[0~j-1]的最長公共前後綴，顯然，next[0]無法求出（因為對於p[0]來說，它左邊並沒有子串），我們需要置為-1。

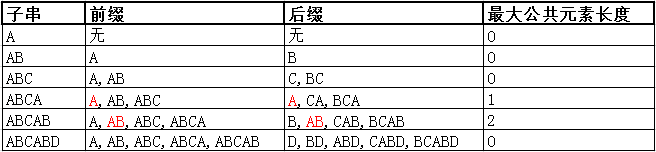
　　我們分解一個next陣列的求解過程，對於字串"ABCABD"，先求其各子串的最長公共前後綴：

　　上表紅色部分即為該子串的最長公共前後綴，根據上表，我們可得next陣列：

　　可以看出，我們就是把next[0]初始化為-1，後面將最大公共元素長度列內的資料依次填入next陣列即可，最大公共元素長度列最後一個數據捨棄。

　　那麼如何用程式求解next陣列？我們下面就來研究一下求法。

　　根據前面的學習可知，如果有k位字首p[0~k-1]和k位字尾p[j-k~j-1]相等（當然，j>k），則有next[j]=k，這就意味著p[j]之前的子串中有長度為k的相同的前後綴，這樣的話，我們在KMP匹配過程中，若在位置j發生了失配，則直接將j移動到next[j]的位置繼續匹配，相當於p字串移動了j-next[j]位，那麼我們如何推出這個next來？我們需要遍歷p這個模式串來確定next陣列：

　　我們首先定義一個k和一個j，j用來從左到右遍歷字串，相當於是p當前子串的字尾的最右字元，而k指向了當前最長字首的最右字元。初始的時候，我們知道next[0]=-1，所以k為-1，j為0。

　　① 若k=-1，說明當前字元j結尾的子串沒有最長前後綴，則next[j + 1] = 0，j，k同時後移。

　　② 若p[j] == p[k]，說明當前字元j結尾子串的字首和字尾匹配了k+1位（由於k指下標，下標從0開始，所以要+1），即next[j+1] = k + 1（其實第①條也可以寫成這樣，畢竟-1+1=0嘛），然後j，k同時後移繼續比較

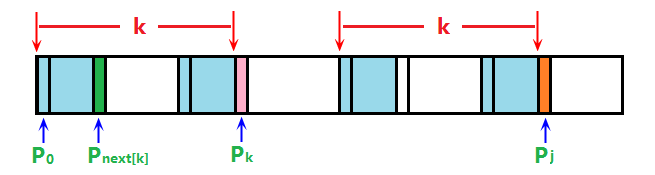
　　③ 若p[j] != p[k]，則說明當前字元j結尾的子串的字尾與字首k不相同，所以需要將k向前移動再重新匹配。那麼k要移動到哪裡呢？我們想一下，既然我們能夠走到p[j]與p[k]進行比較這一步，說明不包括p[k]在內的前k個字元一定與不包括p[j]在內的前k個字元一致，那麼對於子串p[0~k-1]來說，next[k]代表了它的最長公共前後綴的長度，也就是說，不包括p[j]在內的前next[k]個字元一定與整個串的前next[k]個字元相同，比較難理解，我們圖示一下：

　　如圖所示，當p[j]與p[k]不匹配時，兩紅色箭頭所框起來的部分是完全相同的，而對於左邊那一段紅色箭頭框起來的部分，p[k]與p[next[k]]（粉色與綠色）是肯定不相等的，但我們思考一下next[k]的含義是什麼？對的，就是p[k]左邊的串的最大公共前後綴的長度，也就是說，最左邊兩段藍色區域是相同的，那麼由於兩個紅色箭頭框起來的部分相同，所以上圖四片藍色區域均互相相同，那麼既然最右邊的藍色區域與最左邊的藍色區域相等，那麼在p[j]與p[k]不相等的時候，只需要將k重置為next[k]，即可保證此時的k與j仍有公共前後綴。但是需要注意的是，橙色區域一定與粉色區域不相等，粉色區域一定與綠色區域不相等，但是橙色區域與綠色區域關係未知，所以當j與k不匹配時，k應該置為next[k]，繼續比較，再不匹配再置為next[k]……

　　或許結合程式碼看一下就會明白：

void next_arr(char* p, int *next)
{
    int len = strlen(p);
    next[0] = -1;
    int k = -1;
    int j = 0;
    while (j < len - 1)
    {
        //k表示字首最後一位，j表示字尾最後一位
        if (k == -1 || p[j] == p[k])
        {
            // 對應步驟1和2
            ++k;
            ++j;
            next[j] = k;
            // 以上三步可以簡寫成下面這樣，結合自增特點思考一下
            // next[++j] = ++k;
        }
        else // 失配時，移動k指標，即步驟3
        {
            k = next[k];
        }
    }
}

根據next陣列求解字串匹配

　　我們已經學習了next陣列的作用和求法，下面直接給出KMP演算法利用next陣列求解匹配的過程：

　　① 初始時i=j=0，即首部對齊。若s[i] == p[j] ，則字元匹配，i，j分別加1，繼續迴圈執行；

　　② 若j == -1，則說明p串需從頭匹配，則i++，j++，繼續迴圈執行；

　　③ 若s[i] != s[j]，則失配，j = next[j]，繼續迴圈執行。

　　④ 重複這些步驟直至i指標超過了s的最大長度或者j超過了p的最大長度

　　我們上面已經求得"ABCABD"的next陣列為：

　　下面我們根據這個next陣列和上述步驟來圖解一下本章前面的"CADABCABBABCABCABDFR"與"ABCABD"的匹配問題：

　　① 首先i=j=0，對齊首端

　　② 上圖可知，不匹配，則j=next[j]，即j=-1，匹配過程變成如下圖所示：

　　③ 事實上j=-1這一步相當於讓p右移了一位而已，然後按照步驟，j==-1時應該同時移動i，j指標，如圖：

　　④ 這裡匹配，則根據求解步驟，應該同時移動i，j指標，來比較下一對字元，即p[1]=B和s[2]=D，失配，j=next[j]，即j=0，如下圖：

　　⑤ 依然不匹配，則j=next[j]，即j=-1，注意，結合上步，我們這裡連續使用next陣列跳躍了兩次，這裡實際上是效能的損失，可以優化的，這點後面再說，然後此時j==-1，需要同時移動i，j指標，移動後如圖所示：

　　⑥ 此時s[3]與p[0]匹配，指標增加繼續向下比較，直至i=8，j=5時，B和D不匹配了，如圖：

　　⑦ 此時需要使j=next[j]，也就是j=2，相當於p字串右移了3位，然後繼續比較，如下圖：

　　⑧ 此時依然失配，則j=next[j]=0，此時s[8]與p[0]仍然失配（所以說這個next其實還可以繼續優化，不過沒優化也比暴力快得多），j=next[j]=-1，終於可以右移i，j指標了，執行完本步驟以後如下圖所示：

　　⑨ 此時匹配，指標增加，匹配，增加，匹配，增加……直至i=14，j=5時失配，則j=next[j]=2，如下圖：

　　⑩ 此時匹配，指標增加，繼續比較，還匹配，增加，比較，還匹配……直至i=17，j=5，依然是匹配的，然後指標再增加，i=18，j=6，此時發現j指標已經超出p字串的範圍了，結束步驟，並且說明p字串已經成功匹配了s，如下圖：

　　若由於i超出了s的最大長度，且此時j小於p的長度（也就是j沒有過界）則說明未匹配。若匹配成功，則匹配的位置（返回值）為上圖粉色框框的最左邊字元的在s中的位置，即當前i指標的位置減去p的總長度即i-j=12。

　　根據上面的步驟可以看出，我們的i指標自始至終都在向右移動，並沒有產生過回溯，因此相比較暴力解法而言，KMP演算法的效能還是相當高的。

　　kmp匹配的過程程式碼如下：

int kmp_match(char *s, char *p, int *next)
{
    next_arr(p, next);
    int i = 0;
    int j = 0;
    while (s[i] && p[j])
    {
        // j = -1或字元匹配成功指標i，j後移
        if (j == -1 || s[i] == p[j])
        {
            i++;
            j++;
        }
        else
        {
            // 匹配失敗則移動j指標，相當於p字串後移若干位
            j = next[j];
        }
    }
    int len = strlen(p);
    if(j == len) // j與len相等，說明p字串匹配到結尾，即全部匹配成功
        return i - j; // 返回第一個匹配的位置
    return -1; // 無匹配，返回-1
}

　　以上就是kmp演算法的基本內容，可以看出，kmp在處理較大的字串匹配問題時效率是相當高的，並且kmp是ac自動機（Aho-Corasick automaton，多模匹配演算法，後面或許會講到）的基礎知識，理解並掌握kmp是相當重要的。我們之前的講解中說到next陣列的效能問題，其實對於這個next陣列，我們是可以繼續優化的。具體優化原理及方法請看下一小節。

next陣列的優化

　　這個……還是等我有時間再寫吧，不要打我……

　　附加幾個練習題傳送門：

　　以上就是本章全部內容了，資料結構線性表部分全部結束，接下來的章節我們會開始講解另外一種神奇的資料結構——樹，歡迎大家繼續跟進學習交流~