[人工智慧] 粒子群優化演算法 & 差分進化演算法
粒子群優化演算法 & 差分進化演算法
- 前言
- 演算法理論
- 演算法實踐
- 視覺化
前言
演算法理論
粒子群優化演算法
簡介
粒子群優化演算法( Particle Swarm Optimization,PSO)是進化計算的一個分支,是一種模擬自然界的生物活動的隨機搜尋演算法。PSO模擬了自然界鳥群捕食和魚群捕食的過程。通過群體中的協作尋找到問題的全域性最優解。它是1995年由美國學者Eberhart和Kennedy提出的,現在已經廣泛應用於各種工程領域的優化問題之中。
PSO從鳥群覓食模型中得到啟示並用於解決優化問題。PSO中,每個優化問題的解都是搜尋空間中的一隻鳥。我們稱之為“粒子”。所有的粒子都有一個由被優化的函式決定的適應值(fitness value),每個粒子還有一個速度決定他們飛翔的方向和距離。然後粒子們就追隨當前的最優粒子在解空間中搜索。
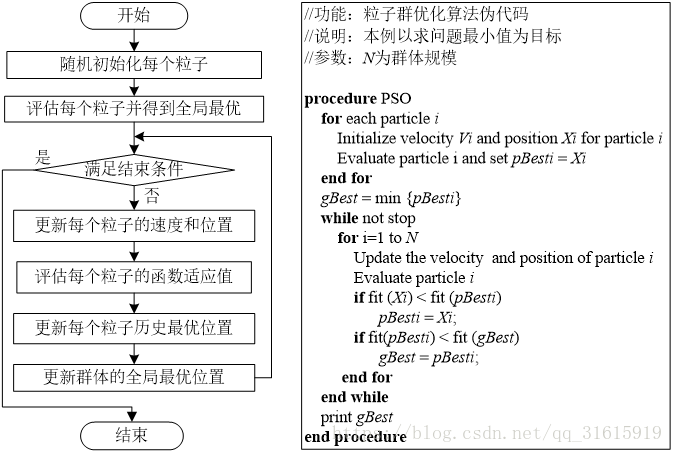
演算法流程及虛擬碼
PSO 初始化為一群隨機粒子(隨機解)。然後通過迭代找到最優解。在每一次迭代中,粒子通過跟蹤兩個”極值”來更新自己。第一個就是粒子本身所找到的最優解,這個解叫做個體極值pBest。另一個極值是整個種群目前找到的最優解,這個極值是全域性極值gBest。另外也可以不用整個種群而只是用其中一部分作為粒子的鄰居,那麼在所有鄰居中的極值就是區域性極值。
更新公式及其引數說明
每個粒子個體的速度和位置更新的公式如下:
v[]和present[]為個體的速度陣列和位置陣列,每個粒子都有它相應的速度和位置,速度的維度和變數的維度保持一致。w為慣性權重,它控制著前一速度對當前速度的影響,用於平衡演算法的探索和開發能力。c1
v[] = w * v[] + c1 * rand() * (pbest[] - present[]) + c2 * rand() * (gbest[] - present[])
present[] = present[] + v[]PSO對種群規模要求不高,一般取20-40就可以達到很好的求解效果,不過對於比較難的問題或者特定類別的問題,粒子數可以取到100或200。
慣性權重我這裡取0.5,代表前一速度對當前速度有一半的貢獻。
c1和c2通常都等於2.0,代表著對兩個引導方向的同等重視 。
終止條件決定演算法執行的結束,由具體的應用和問題本身確定。有幾種做法:
(1)將最大迴圈數設定為500,1000,5000,或者最大的函式評估次數,等等;
(2)也可以使用演算法求解得到一個可接受的解作為終止條件;
(3)或者是當演算法在很長一段迭代中沒有得到任何改善,則可以終止演算法.
差分進化演算法
簡介
差分進化演算法(DE)是Rainer Storn 和Kenneth Price在1996 年為求解切比雪夫多項式而提出。DE是一種隨機的並行直接搜尋演算法,它可對非線性不可微連續空間函式進行最小化,以其易用性、穩健性和強大的全域性尋優能力在多個領域取得成功。
DE也是基於群體的啟發式搜尋演算法,群中的每個個體對應一個解向量。差分進化演算法的進化流程則與遺傳演算法非常類似,都包括變異、雜交和選擇操作,但這些操作的具體定義與遺傳演算法有所不同。
演算法流程及偽碼
DE演算法通過採用浮點向量進行編碼生成種群個體。
在DE演算法尋優的過程中,
首先,從父代個體間選擇兩個個體進行向量做差生成差分向量;
其次,選擇另外一個個體與差分向量求和生成實驗個體;
然後,對父代個體與相應的實驗個體進行交叉操作,生成新的子代個體;
最後在父代個體和子代個體之間進行選擇操作,將符合要求的個體儲存到下一代群體中去。
具體流程如下:
(1)確定差分進化演算法控制引數,確定適應度函式。差分進化演算法控制引數包括:種群大小NP、縮放因子F與雜交概率CR。
(2)隨機產生初始種群。
(3)對初始種群進行評價,即計算初始種群中每個個體的適應度值。
(4)判斷是否達到終止條件或進化代數達到最大。若是,則終止進化,將得到最佳個體作為最優解輸出;若否,繼續。
(5)進行變異和交叉操作,得到中間種群。
(6)在原種群和中間種群中選擇個體,得到新一代種群。
(7)進化代數g=g+1,轉步驟(4)
更新公式及其引數說明
差異演化演算法主要涉及群體規模M 、縮放因子F以及交叉概率CR三個引數的設定。
M:一般介於5×n 與10×n 之間, 但不能少於4, 否則無法進行變異操作,n是維度;
F :一般在[ 0, 2 ]之間選擇, 通常取0. 5;
CR:一般在[ 0, 1 ]之間選擇, 比較好的選擇應在0. 3 左右, CR 大些收斂速度會加快, 但易發生早熟現象。
演算法實踐
粒子群優化演算法
- 隨機初始化每個粒子
srand((unsigned)time(NULL));
int population = static_cast<int>(getParameters(tr("population")));//種群大小
int dimension = static_cast<int>(getParameters(tr("dimension")));//維度
int generation = static_cast<int>(getParameters(tr("generation")));//迭代次數
double lowbounding = getParameters(tr("lowbounding"));
double upbounding = getParameters(tr("upbounding"));
group.clear();
group.resize(generation,std::vector<std::vector<double> >(population,
std::vector<double>(dimension,0.0)));
for (int i = 0; i < population; i++) {
for (int j = 0; j < dimension; j++) {
group[0][i][j] = lowbounding +
(double)(rand() / (double)RAND_MAX) * (upbounding - lowbounding);
}
}- 更新每個粒子的速度和位置
void PSOAlgorithm::update(int curGeneration)
{//更新速度和位置
int dimension = static_cast<int>(getParameters(tr("dimension")));
int population = static_cast<int>(getParameters(tr("population")));
double w = getParameters(tr("w"));//慣性權重
double c1 = getParameters(tr("c1"));//加速係數
double c2 = getParameters(tr("c2"));//加速係數
double upbounding = getParameters(tr("upbounding"));//上界
double lowbounding = getParameters(tr("lowbounding"));//下界
for(auto i = 0;i < population;++i){
for(auto j = 0;j < dimension;++j){
double pre = velocity[i][j];
//更新速度
velocity[i][j] = w*pre +
c1*(double)(rand()/(double)RAND_MAX)*
(pBest[i][j] - group[curGeneration - 1][i][j])
+
c2*(double)(rand()/(double)RAND_MAX)*
(gBest[j] - group[curGeneration - 1][i][j]);
if(velocity[i][j] > 200)velocity[i][j] = 200;
//位置更新
group[curGeneration][i][j] = group[curGeneration-1][i][j] + velocity[i][j];
//邊界處理
if(group[curGeneration][i][j] > upbounding)
group[curGeneration][i][j] = upbounding;
if(group[curGeneration][i][j] < lowbounding)
group[curGeneration][i][j] = lowbounding;
}
}
}- 更新每個粒子的歷史最優和全域性最優、
void PSOAlgorithm::curAndgloBest(int curGeneration)
{//計算當前最優解和全域性最優解
int population = static_cast<int>(getParameters(tr("population")));
int dimension = static_cast<int>(getParameters(tr("dimension")));
int func_num = static_cast<int>(getParameters(tr("function")));//函式編號
for (auto i = 0; i < population; ++i) {
double value = functions(group[curGeneration][i], func_num, dimension);
if (value < functions(pBest[i], func_num, dimension))
pBest[i] = group[curGeneration][i];
if (functions(pBest[i], func_num, dimension) < functions(gBest, func_num, dimension)){
gBest = pBest[i];
bestValue.first = i;
bestValue.second = functions(pBest[i], func_num, dimension);
}
}
}- 演算法核心
void PSOAlgorithm::process()
{
curAndgloBest(0);//計算初始代最優解
int generation = static_cast<int>(getParameters(tr("generation")));//迭代次數
for (auto current = 1; current < generation; ++current) {
update(current);
curAndgloBest(current);
calcCurrentValue(pBest);
if(generation <= 100 || (generation > 100 && generation % 2 == 0))
emit frameUpdate(avgValue,currentValue,minY,maxY,current,generation,bestValue);
}
emit processFinished(getResult(gBest));
}粒子群優化演算法
- 隨機產生初始種群
srand((unsigned)time(NULL));
int population = static_cast<int>(getParameters(tr("population")));//種群大小
int dimension = static_cast<int>(getParameters(tr("dimension")));//維度
int generation = static_cast<int>(getParameters(tr("generation")));//迭代次數
double lowbounding = getParameters(tr("lowbounding"));
double upbounding = getParameters(tr("upbounding"));
group.clear();
group.resize(generation,std::vector<std::vector<double> >(population,
std::vector<double>(dimension,0.0)));
for (int i = 0; i < population; i++) {
for (int j = 0; j < dimension; j++) {
group[0][i][j] = lowbounding +
(double)(rand() / (double)RAND_MAX) * (upbounding - lowbounding);
}
}- 核心演算法
void DEAlgorithm::process()
{
int population = static_cast<int>(getParameters(tr("population")));//種群大小
int dimension = static_cast<int>(getParameters(tr("dimension")));//維度
int generation = static_cast<int>(getParameters(tr("generation")));//迭代次數
double lowbounding = getParameters(tr("lowbounding"));
double upbounding = getParameters(tr("upbounding"));
double DE_F = getParameters(tr("F"));//縮放因子
double DE_CR = getParameters(tr("CR"));//交叉概率
int func_num = static_cast<int>(getParameters(tr("function")));//函式編號
double bestSolution = 100000000;//目前全域性最優解
//開始迭代
for(auto t=1;t<generation;t++){
//變異
for(int i=0;i<population;i++){
//隨機選三個向量
std::vector<bool> selected(population,false);
selected[i] = true;
int pick[3];
for(auto k=0;k<3;k++){
pick[k] = rand() % population;
while(selected[pick[k]])pick[k] = rand() % population;
selected[pick[k]] = true;
}
for(auto j=0;j<dimension;j++){
//變異操作公式
group[t][i][j] = group[t-1][pick[0]][j] +
DE_F * (group[t-1][pick[1]][j] - group[t-1][pick[2]][j]);
//邊界處理
if(group[t][i][j]<lowbounding) group[t][i][j] = lowbounding;
else if(group[t][i][j]>upbounding) group[t][i][j] = upbounding;
}
}
//交叉
for(auto i=0;i<population;i++){
for(auto j=0;j<dimension;j++){
if(((rand() % 100) / 100.0) <= DE_CR || j == (rand() % dimension))
group[t][i][j] = group[t][i][j];
else
group[t][i][j] = group[t-1][i][j];
}
}
//選擇替換,貪心策略
for(auto i=0;i<population;i++){
if(functions(group[t][i],func_num,dimension) <=
functions(group[t-1][i],func_num,dimension)){
group[t][i] = group[t][i];
bestSolution =
bestSolution < functions(group[t][i],func_num,dimension)
? bestSolution : functions(group[t][i],func_num,dimension);
if(bestSolution < functions(group[t][i],func_num,dimension)){
bestValue.first = i;
bestValue.second = bestSolution;
solution = group[t][i];
}
}
else{
group[t][i] = group[t-1][i];
}
}
//計算當前種群的全部值
calcCurrentValue(group[t]);
if(generation > 300 && generation % 2 == 0){
emit frameUpdate(avgValue,currentValue,minY,maxY,t,generation,bestValue);
}
else{
emit frameUpdate(avgValue,currentValue,minY,maxY,t,generation,bestValue);
}
}
emit processFinished(getResult(solution));
}以上只是演算法的核心部分,更多的細節請看原始碼。
視覺化
用Qt做了個視覺化,可以調節引數,顯示了種群個體的每個個體的適應值以及整個種群的適應值收斂曲線。
粒子群演算法:
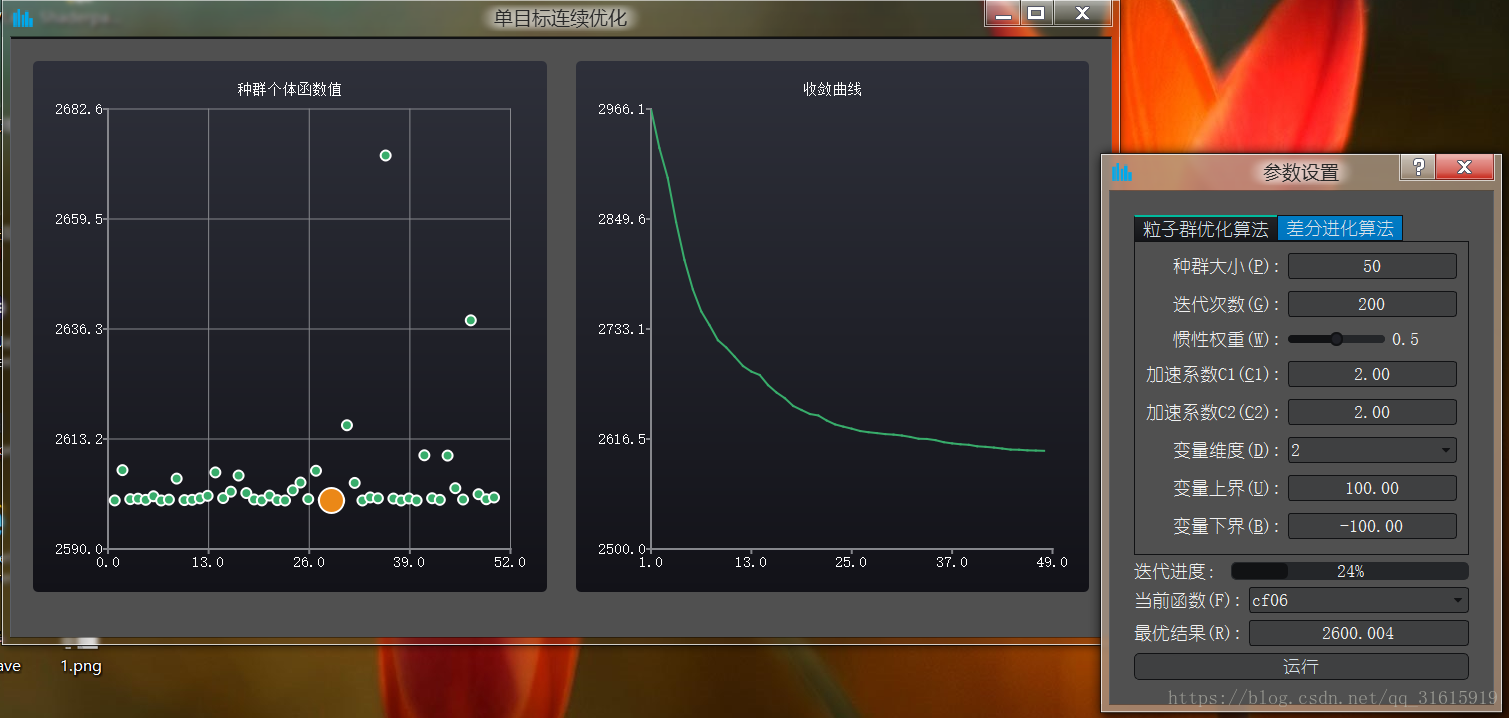
可以看到最後粒子都收斂了,在同一條直線上:
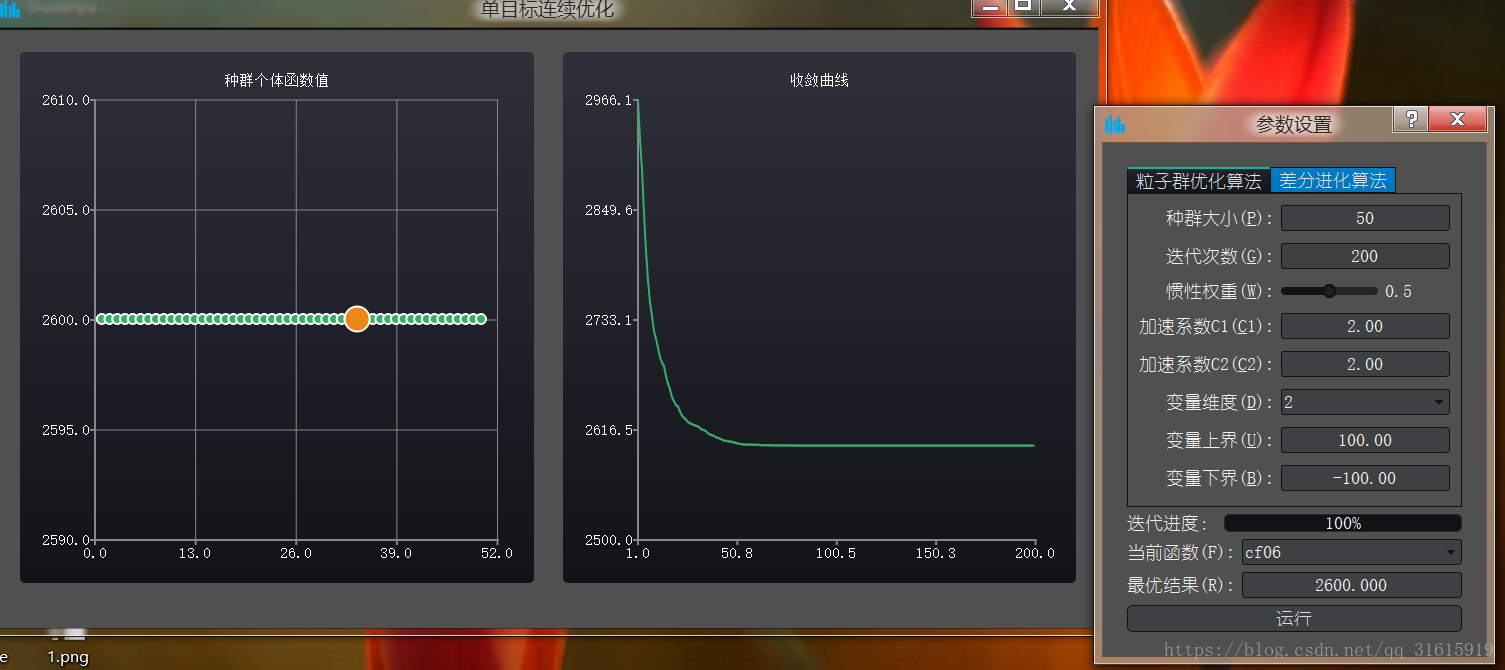
差分進化演算法:
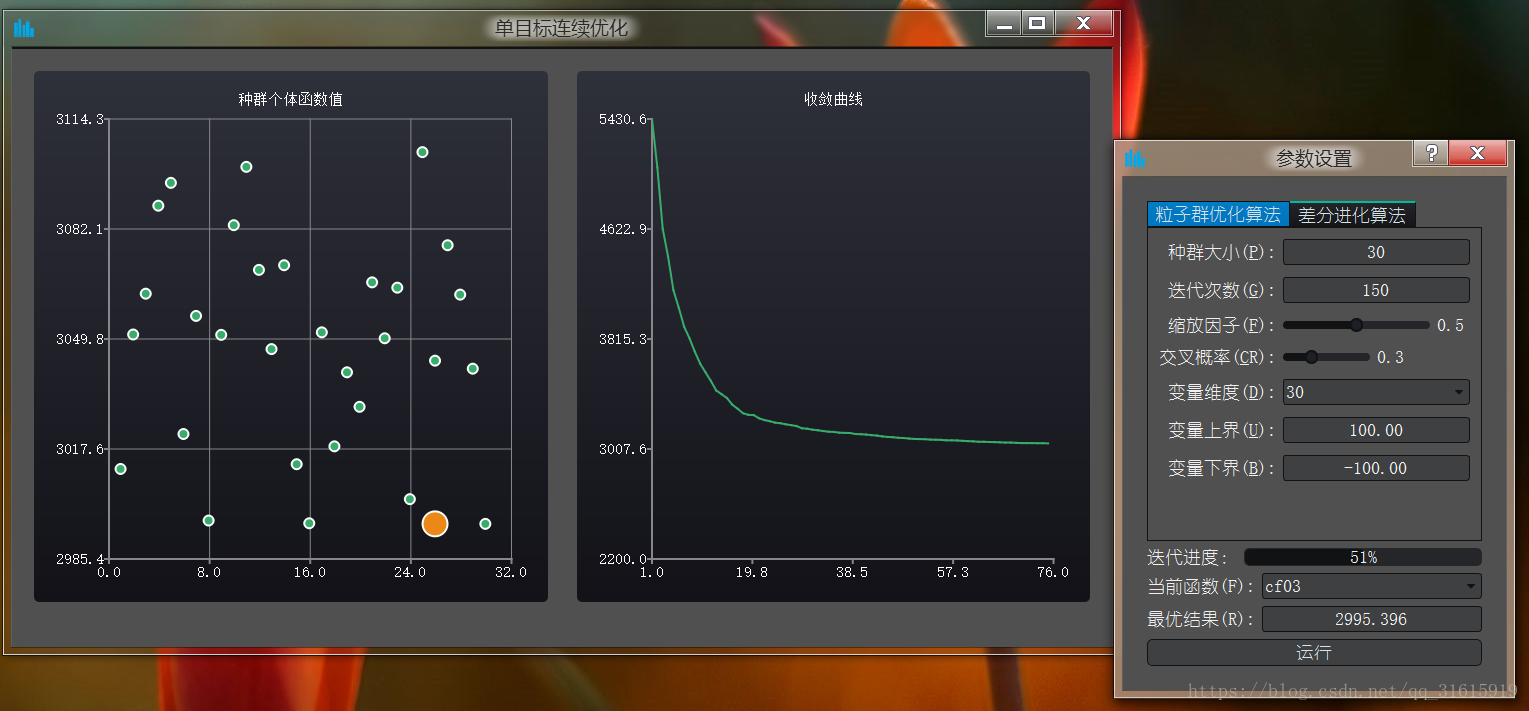
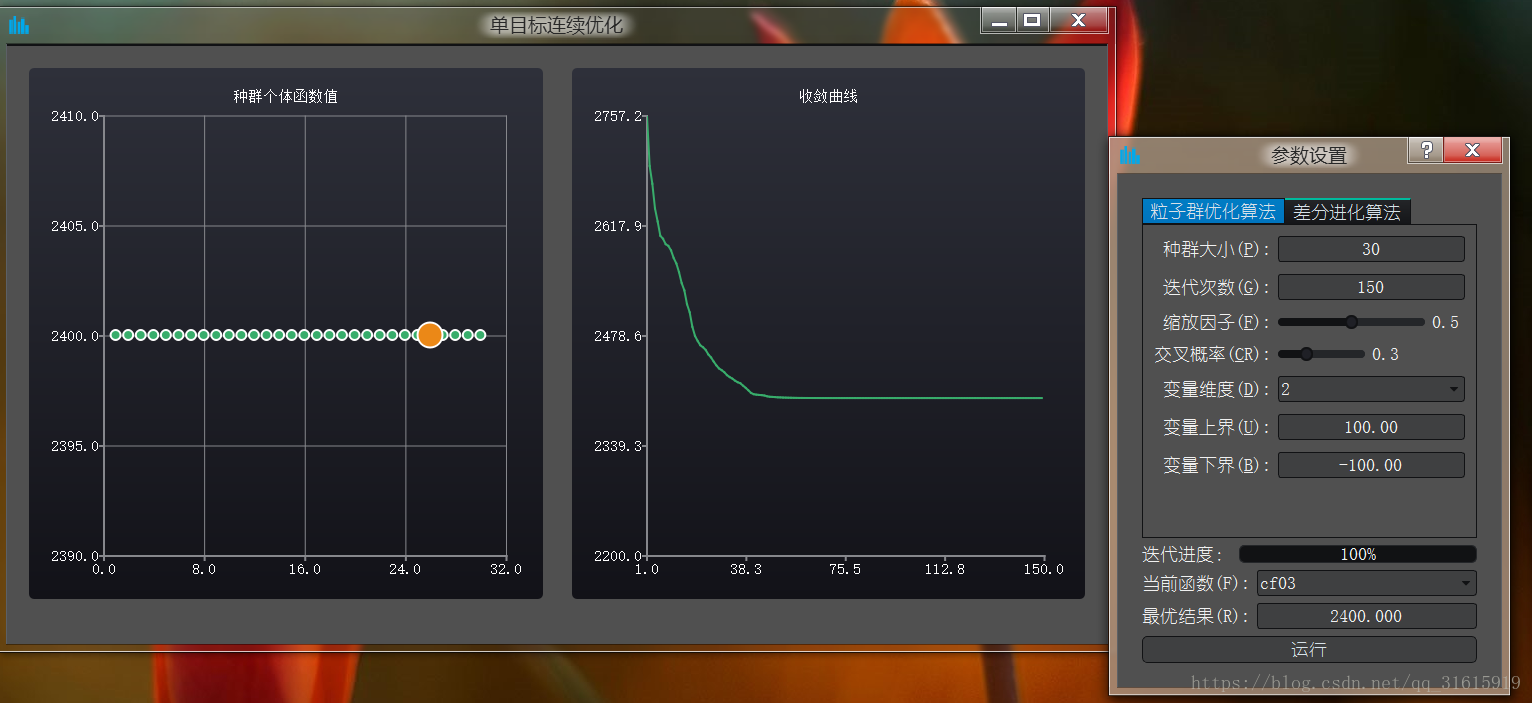
總的來說,差分進化演算法略佔優勢,收斂的速度也比較快,粒子群演算法比較沒那麼穩定.
相關推薦
[人工智慧] 粒子群優化演算法 & 差分進化演算法
粒子群優化演算法 & 差分進化演算法 前言 演算法理論 演算法實踐 視覺化 前言 演算法理論 粒子群優化演算法 簡介 粒子群優化演算法( Particle Swarm Optimization,PSO)是進化計算的一個分支,是一種模擬
優化演算法——差分進化演算法(DE)
一、差分進化演算法的介紹 差分進化演算法(Differential Evolution, DE)是一種基於群體差異的啟發式隨機搜尋演算法,該演算法是由R.Storn和K.Price為求解Chebyshev多項式而提出的。DE演算法也屬於智慧優化演算法,與前面的
遺傳演算法 差分進化演算法 粒子群優化演算法區別
一 遺傳演算法 遺傳演算法(GA)作為一種經典的進化演算法,自 Holland提出之後在國際上已經形成了一個比較活躍的研究領域. 人們對 GA 進行了大量的研究,提出了各種改進演算法用於提高演算法的收斂速度和精確性. 遺傳演算法採用選擇,交叉,變異操作,在問題空間搜尋最優解.
差分進化演算法DE優化BPNN
(一)DE的基本原理 主要操作:變異 - 交叉 - 選擇 (二)DE優化BPNN %載入資料 data = csvread('D:\matlab2016a\OA\sample.csv'); %劃分資料集 rv = rand(1,size(data,1)); [val
差分進化演算法 C語言實現
之前的一篇中貼出了自己研究生期間C實現的基本粒子群演算法,執行速度顯然要比其他的高階語言快,這也是各個程式語言之間的差別,現在對於曾經輝煌過的差分進化演算法進行C語言實現。變異策略採用DE/rand/1,這個是最常見的。有錯誤之處請之處。 /***************D
差分進化演算法DE-python實現
下面是python 實現 # -*- coding: cp936 -*- import numpy as np import matplotlib.pyplot as plt import math import random # Rastrigr 函式 def ob
差分進化演算法總結
基本介紹 DE(Differential Evolution)演算法於1997年由Rainer Storn和Kenneth Price在遺傳演算法等進化思想的基礎上提出的,本質是一種多目標(連續變數)優化演算法,用於求解多維空間中整體最優解。其基本思想即是來源於
遺傳演算法與差分進化演算法總結比較
遺傳演算法 遺傳演算法的基本原理: 遺傳演算法是一種基於生物進化原理構想出來的搜尋最優解的仿生演算法,它是模擬基因重 組與進化的自然過程,把待解決問題的引數編成二進位制碼或十進位制碼(也可編成其他進
numba版 自適應差分進化演算法 速度超快 可以求解約束問題
import numpy as np from numba import njit from math import cos,pi random=np.random.random randint=np.random.randint @njit def fitn
差分進化演算法(Differential Evolution)
差分進化演算法(Differential Evolution,DE)和GA,PSO,ACO等進化演算法一樣,都是基於群體智慧的隨機並行優化演算法,通過模仿生物群體內個體間的合作與競爭產生的啟發式群體智慧來指導優化搜尋。 運算元課上我講的PPT,主題是查分演化計
差分進化演算法介紹及matlab實現
引言 差分進化演算法是基於群體智慧理論的優化演算法,是通過群體內個體間的合作與競爭而產生的智慧優化搜尋演算法,它保留了基於種群的全域性搜尋策略,採用實數編碼、基於差分的簡單變異操作和“一對一”的競爭生存策略,降低了進化計算操作的複雜性。 差分進化演算法的原理 差分進化演算法是一種自組織最小化方法,利用種群
粒子群優化演算法
粒子群優化演算法是模仿生物社會系統而設計的,更確切的說,是由簡單個體組成的群體與環境以及個體之間的互動行為,是一種基於群智慧方法的進化計算技術。 粒子群演算法源於鳥群捕食行為的模擬。一群鳥在一個固定的區域裡隨機搜尋區域裡唯一的一塊食物,所有的鳥都不知到食物在哪裡,但是他們知道自己當前所處的位置離
粒子群優化演算法 PSO
分享一下我老師大神的人工智慧教程!零基礎,通俗易懂!http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識,造福人民,實現我們中華民族偉大復興!
粒子群優化演算法(PSO)簡介及MATLAB實現
目錄 粒子群優化演算法概述 • 粒子群優化(PSO, particle swarm optimization)演算法是計算智慧領域,除了蟻群演算法,魚群演算法之外的一種群體智慧的優化演算法,該演算法最早由Kennedy和Eberhart在1995年提出的,
matlab學習筆記(1)——粒子群優化演算法(PSO)的程式實現
本文內容參考matlab R2016a完全自學一本通。 粒子群優化演算法(PSO)屬於進化演算法的一種,它從隨機解出發,通過迭代找到最優解。該演算法通過適應度來評價解的品質,並通過追隨當前搜尋到的最優值來尋找全域性最優。 假設在一個D維的目標搜尋空間
粒子群優化演算法(PSO)之基於離散化的特徵選擇(FS)(二)
作者:Geppetto 前面我們介紹了特徵選擇(Feature Selection,FS)與離散化資料的重要性,總覽的介紹了PSO在FS中的重要性和一些常用的方法。今天講一講FS與離散化的背景,介紹本文所採用的基於熵的切割點和最小描述長度原則(MDLP
MATLAB粒子群優化演算法實現(PSO)
PSO(PSO——Particle Swarm Optimization)(基於種群的隨機優化技術演算法) 粒子群演算法模仿昆蟲、獸群、鳥群和魚群等的群集行為,這些群體按照一種合作的方式尋找食物,群體
PSO-粒子群優化演算法
PSO 演算法 粒子群優化演算法 PSO 1. 常見的群體智慧優化演算法分類 常見的群體智慧優化演算法主要有如下幾類: (1)蟻群演算法(Ant Colony Optimization,簡稱ACO)[1992年提出]; (2)粒子群優化演算法(Particle
[Algorithm] 群體智慧優化演算法之粒子群優化演算法
%% 該檔案演示基於TSP-PSO演算法 clc;clear %% 載入資料 data=load('eil51.txt') cityCoor=[data(:,2) data(:,3)];%城市座標矩陣 figure plot(cityCoor(:,1),cityCoor(:,2),'m
粒子群優化演算法對BP神經網路優化 Matlab實現
1、粒子群優化演算法 粒子群演算法(particle swarm optimization,PSO)由Kennedy和Eberhart在1995年提出,該演算法模擬鳥叢集飛行覓食的行為,鳥之間通過集體的協作使群體達到最優目的,是一種基於 Swarm Inteligence的優化方法。同遺傳演算法類似,也是一種