詳解 01,完全,多重揹包
揹包問題泛指以下這一種問題:
給定一組有固定價值和固定重量的物品,以及一個已知最大承重量的揹包,求在不超過揹包最大承重量的前提下,能放進揹包裡面的物品的最大總價值。
這一類問題是典型的使用動態規劃解決的問題,我們可以把揹包問題分成3種不同的子問題:0-1揹包問題、完全揹包和多重揹包問題。下面對這三種問題分別進行討論。
1.0-1揹包問題
0-1揹包問題是指每一種物品都只有一件,可以選擇放或者不放。現在假設有n件物品,揹包承重為m。
對於這種問題,我們可以採用一個二維陣列去解決:f[i][j],其中i代表加入揹包的是前i件物品,j表示揹包的承重,f[i][j]表示當前狀態下能放進揹包裡面的物品的最大總價值。那麼,f[n][m]就是我們的最終結果了。
採用動態規劃,必須要知道初始狀態和狀態轉移方程。初始狀態很容易就能知道,那麼狀態轉移方程如何求呢?對於一件物品,我們有放進或者不放進揹包兩種選擇:
(1)假如我們放進揹包,f[i][j] = f[i - 1][j - weight[i]] + value[i],這裡的f[i - 1][j - weight[i]] + value[i]應該這麼理解:在沒放這件物品之前的狀態值加上要放進去這件物品的價值。而對於f[i - 1][j - weight[i]]這部分,i - 1很容易理解,關鍵是 j - weight[i]這裡,我們要明白:要把這件物品放進揹包,就得在揹包裡面預留這一部分空間。
(2)假如我們不放進揹包,f[i][j] = f[i - 1][j],這個很容易理解。
因此,我們的狀態轉移方程就是:f[i][j] = max(f[i][j] = f[i - 1][j] , f[i - 1][j - weight[i]] + value[i])
當然,還有一種特殊的情況,就是揹包放不下當前這一件物品,這種情況下f[i][j] = f[i - 1][j]。
下面是實現的程式碼:

#include <iostream> #define V 500 using namespace std; int weight[20 + 1]; int value[20 + 1]; int f[20 + 1][V + 1]; int main() {int n, m; cout << "請輸入物品個數:"; cin >> n; cout << "請分別輸入" << n << "個物品的重量和價值:" << endl; for (int i = 1; i <= n; i++) { cin >> weight[i] >> value[i]; } cout << "請輸入揹包容量:"; cin >> m; for (int i = 1; i <= n; i++) { for (int j = 1; j <= m; j++) { if (weight[i] > j) { f[i][j] = f[i - 1][j]; } else { f[i][j] = f[i - 1][j] > f[i - 1][j - weight[i]] + value[i] ? f[i - 1][j] : f[i - 1][j - weight[i]] + value[i]; } } } cout << "揹包能放的最大價值為:" << f[n][m] << endl; }

特別的是,0-1揹包問題還有一種更加節省空間的方法,那就是採用一維陣列去解決,下面是程式碼:

#include <iostream> #define V 500 using namespace std; int weight[20 + 1]; int value[20 + 1]; int f[V + 1]; int main() { int n, m; cout << "請輸入物品個數:"; cin >> n; cout << "請分別輸入" << n << "個物品的重量和價值:" << endl; for (int i = 1; i <= n; i++) { cin >> weight[i] >> value[i]; } cout << "請輸入揹包容量:"; cin >> m; for (int i = 1; i <= n; i++) { for (int j = m; j >= 1; j--) { if (weight[i] <= j) { f[j] = f[j] > f[j - weight[i]] + value[i] ? f[j] : f[j - weight[i]] + value[i]; } } } cout << "揹包能放的最大價值為:" << f[m] << endl; }

我看過很多部落格的描述,講得都不太清楚:為什麼要把第二層迴圈顛倒過來呢?我認為要理解這種方法,用圖是最合適不過了,我在另外一個部落格(http://blog.csdn.net/mu399/article/details/7722810)找到了這樣一個圖:
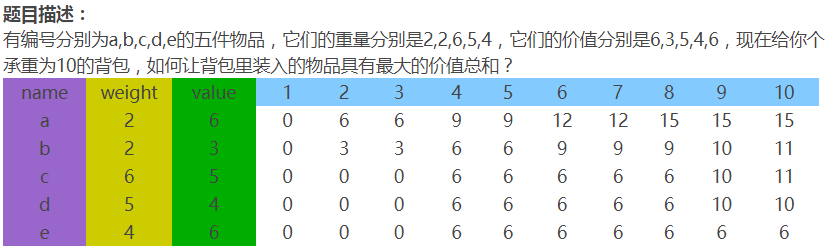
這個表格對於理解0-1揹包問題很有用,我們利用它來理解一下為什麼要把第二層迴圈顛倒這個問題。考慮d9這一項,要求出這個狀態,我們有可能利用到的就是e1到e8這8個狀態,當我們把第二層迴圈顛倒過來時,當我們要求f[j]時,f[j -1]到f[1]還儲存著下面一行的狀態,因此可以採用一維陣列解決。我們可以考慮一下假如不把第二層迴圈顛倒,當要求f[j]時,f[j - 1]到f[1]已經是同一行的狀態了,根本沒法求。
我在LeetCode上也曾做過類似的題目——120 Triangle(https://leetcode.com/problems/triangle/description/),也是把二維陣列簡化為一維陣列去解決問題。
更新:

for (int i = 1; i <= n; i++) { for (int j = m; j >= 1; j--) { if (weight[i] <= j) { f[j] = f[j] > f[j - weight[i]] + value[i] ? f[j] : f[j - weight[i]] + value[i]; } } }

這是0-1揹包最重要的部分,可以把它改為下面的更簡潔的版本:
for (int i = 1; i <= n; i++) { for (int j = m; j >= weight[i]; j--) { f[j] = f[j] > f[j - weight[i]] + value[i] ? f[j] : f[j - weight[i]] + value[i]; } }
2.完全揹包問題
完全揹包問題是指每種物品都有無限件,具體的解法我也解釋不清楚,只能先放程式碼,談談我的理解了:

#include <iostream> #define V 500 using namespace std; int weight[20 + 1]; int value[20 + 1]; int f[V + 1]; int max(int a, int b) { return a > b ? a : b; } int main() { int n, m; cout << "請輸入物品個數:"; cin >> n; cout << "請分別輸入" << n << "個物品的重量和價值:" << endl; for (int i = 1; i <= n; i++) { cin >> weight[i] >> value[i]; } cout << "請輸入揹包容量:"; cin >> m; for (int i = 1; i <= n; i++) { for (int j = weight[i]; j <= m; j++) { f[j] = max(f[j], f[j - weight[i]] + value[i]); } } cout << "揹包能放的最大價值為:" << f[m] << endl; }

i=1時,計算只放第一件物品的最大價值。
i=2時,計算加上第二件物品的最大價值(在只放第一件物品的前提下)
以此類推……
值得注意的是,第二層迴圈要從j=weight[i]開始,這個稍微理解一下即可。
我在別的部落格看到了一段分析0-1揹包問題和完全揹包問題區別的話,覺得對理解這兩個問題很有幫助,因此截圖如下:
3.多重揹包問題
多重揹包問題限定了一種物品的個數,解決多重揹包問題,只需要把它轉化為0-1揹包問題即可。比如,有2件價值為5,重量為2的同一物品,我們就可以分為物品a和物品b,a和b的價值都為5,重量都為2,但我們把它們視作不同的物品。
程式碼如下:

#include <iostream> using namespace std; #define V 1000 int weight[50 + 1]; int value[50 + 1]; int num[20 + 1]; int f[V + 1]; int max(int a, int b) { return a > b ? a : b; } int main() { int n, m; cout << "請輸入物品個數:"; cin >> n; cout << "請分別輸入" << n << "個物品的重量、價值和數量:" << endl; for (int i = 1; i <= n; i++) { cin >> weight[i] >> value[i] >> num[i]; } int k = n + 1; for (int i = 1; i <= n; i++) { while (num[i] != 1) { weight[k] = weight[i]; value[k] = value[i]; k++; num[i]--; } } cout << "請輸入揹包容量:"; cin >> m; for (int i = 1; i <= k; i++) { for (int j = m; j >= 1; j--) { if (weight[i] <= j) f[j] = max(f[j], f[j - weight[i]] + value[i]); } } cout << "揹包能放的最大價值為:" << f[m] << endl; }
相關推薦
詳解 01,完全,多重揹包
揹包問題泛指以下這一種問題: 給定一組有固定價值和固定重量的物品,以及一個已知最大承重量的揹包,求在不超過揹包最大承重量的前提下,能放進揹包裡面的物品的最大總價值。 這一類問題是典型的使用動態規劃解決的問題,我們可以把揹包問題分成3種不同的子問題:0-1揹包問題、完全揹包和多重揹包問題。下面對這三種問題分別進
揹包模板(01,完全,多重揹包的二進位制優化和單調佇列優化
揹包問題 1,01揹包 揹包問題的基礎,總體積為V的揹包,有n件體積v【i】,價值w【i】的物品,求能裝物品的最大總價值 void zero(int v,int w) { for(int j=V;j>=v;j--) { dp[j]=max(dp[j],dp[j
01揹包的四種解法詳解:動態規劃,貪心法,回溯法,優先佇列式分支限界法(C語言編寫)
最近剛完成了演算法課程設計,題目是用多種解法解決01揹包問題,經過一番探索,終於成功的用四種方法完成了本次實驗,下面記錄分享一下成果: 首先解釋下什麼是01揹包問題:給定一組共n個物品,每種物品都有自己的重量wi, i=1~n和價值vi, i=1~n,在限定的總重量(揹包的
背包問題專欄(01,完全,多重)
c++ gif 什麽 就是 pri tps 需要 info 方程 本題的模板是套用了 A.S.KirigiriKyouko 的模板。請dalao見諒 一、01背包 有N件物品和一個容量為V的背包。第i件物品的價格(即體積,下同)是w[i],價值是c[i]。求解將哪些
Python模塊詳解以及import本質,獲得文件當前路徑os.path.abspath,獲得文件的父目錄os.path.dirname,放到系統變量的第一位sys.path.insert(0,x)
alt 獲取 詳解 nbsp spa 絕對路徑 解釋 系統 port 模塊介紹 1、定義: 模塊:用來從邏輯上組織python代碼(變量,函數,類,邏輯:實現一個功能),本質就是.py結尾的python文件(文件名:test.py,對應的模塊名:test) 包:用來從邏輯上
守護進程詳解及創建,daemon()使用
blog zomb 錯誤信息 數據庫 net == span 孤兒進程 null 一,守護進程概述 Linux Daemon(守護進程)是運行在後臺的一種特殊進程。它獨立於控制終端並且周期性地執行某種任務或等待處理某些發生的事件。它不需要用戶輸入就能運行而 且提供某種
Linux基本常用命令之ls詳解(含date,cal)
Linux基礎【1】顯示日期的指令:date示例:(1)#date +%Y/%m/%d結果:2018/02/27(2)#date +%H:%M結果:10:48【2】顯示日歷的指令:cal格式:cal [month] [year]示例:(1)#cal 2 2018(2)#cal 13 2018結果:cal:il
UX術語幸運飛艇源碼下載詳解:任務流,用戶流,流程圖以及其它全新術語
希望 演示 重要 職位 flow 重新 生成 img 所有 用戶幸運飛艇源碼下載【大神源碼論壇】dsluntan.com 【布丁源碼論壇】budingbbs.com 企娥3393756370 體驗擁有一長串專業的術語和可交付內容。當在線查看UX相關職位描述時,所羅列的這類
NGINX源碼安裝配置詳解(./configure),最全解析
unzip roo without rpc服務 所有 googl 版本 並且 大文件 NGINX ./configure詳解 在"./configure"配置中,"--with"表示啟用模塊,也就是說這些模塊在編譯時不會自動構建&qu
詳解萬向鎖,尤拉旋轉角,slam中萬向鎖的理解
第一步:先花10分鐘看一下這個下面是的視訊,絕對有用! http://v.youku.com/v_show/id_XNzkyOTIyMTI=.html 萬向鎖含義:當兩個旋轉軸重合時,導致只剩了2個旋轉,2個旋轉不能將所有情況進行描述。 第二步: 看視訊,如果還不理解,請拿出手機,跟
tensorflow詳解-tf.nn.conv2d(),tf.nn.max_pool()
tf.nn.conv2d() 函式來計算卷積,weights 作為濾波器,[1, 2, 2, 1] 作為 strides。TensorFlow 對每一個 input 維度使用一個單獨的 stride 引數,[batch, input_
詳解mybatis的create,retrieve,delete,update返回值。
首先是select User user = new User(); user.setName("l2"); user.setPassword("444"); int i = userMapper.addUser(user);
Redis詳解 - SpringBoot整合Redis,RedisTemplate和註解兩種方式的使用
本文主要講 Redis 的使用,如何與 SpringBoot 專案整合,如何使用註解方式和 RedisTemplate 方式實現快取。最後會給一個用 Redis 實現分散式鎖,用在秒殺系統中的案例。 更多 Redis 的實際運用場景請關注開源專案 coderiver 專案地址:github.com/cac
深度學習 --- 模擬退火演算法詳解(Simulated Annealing, SA)
上一節我們深入探討了,Hopfield神經網路的性質,介紹了吸引子和其他的一些性質,而且引出了偽吸引子,因為偽吸引子的存在導致Hopfield神經網路正確率下降,因此本節致力於解決偽吸引子的存在。在講解方法之前我們需要再次理解一些什麼是偽吸引子,他到底是如何產生的? 簡單來說說就是網路動態轉
舉例詳解java例項變數,靜態變數,區域性變數
public class Variable { public int m,n;//對子類可見的例項變數 private double k;//只對本類可見的例項變數,一般情況下,設為私有,通過使用訪問修飾符來被子類使用。 public static String P;//靜態變數(
HDU-2191-悼念512汶川大地震遇難同胞——珍惜現在,感恩生活(多重揹包+dp)
急!災區的食物依然短缺! 為了挽救災區同胞的生命,心繫災區同胞的你準備自己採購一些糧食支援災區,現在假設你一共有資金n元,而市場有m種大米,每種大米都是袋裝產品,其價格不等,並且只能整袋購買。 請問:你用有限的資金最多能採購多少公斤糧食呢? 後記: 人生是一個充滿了變數的生命過程,天災、人禍、病痛是
詳解>>堆,棧,堆疊,佇列
1.堆 堆就是一棵完全二叉樹 具有以下特性 在程式執行時分配記憶體(動態分配記憶體) 應用程式在執行時向作業系統申請空間 2.棧(堆疊) 運算受限制的單鏈表,只能從一個方向操作 像是一個桶,只能從開口方向放入或者拿出資料,開口方向為棧頂,不開口方向棧底
前端模組化開發規範的終結者Webpack詳解(純乾貨,不套路)
可謂集CommonJS、AMD、ES6等多種特性於一身,靈活、易用、高擴充套件性、效能優越。 核心配置 以下是webpack的幾個核心配置節: 節點 說明 entry 指定要打包的檔案
哨兵2資料‘檔名’詳解(吐血整體,僅供參考)
哨兵2資料檔名詳解 Sentinel-2 Level-1C products: (2016年12月6日之後生成的Sentinel-2 Level-1C產品的新格式命名約定) .zip解壓後為.SAFE檔案 S2A_MSIL1C_20170105T013442_
HBase基本資料操作詳解【完整版,絕對精品】
引言 之前詳細寫了一篇HBase過濾器的文章,今天把基礎的表和資料相關操作補上。 本文件參考最新(截止2014年7月16日)的官方Ref Guide、Developer API編寫。 所有程式碼均基於“hbase 0.96.2-hadoop2”版本編寫,均實測通過。 歡迎轉載
