SICP習題解答2.1-2.6
ex2.1-2.4
#lang racket ; exercise 2.1 (define (make-rat n d) (define g (gcd n d)) (let ((g1 (if (< d 0) (- g) g))) (cons (/ n g1) (/ d g1)))) (define (gcd a b) ;; 返回正最大公約數 (if (= b 0) (if (< a 0) (- a) a) (gcd b (remainder a b)))) ; exercise 2.2 (define (make-segment s e) (cons s e)) (define (start-segment seg) (car seg)) (define (end-segment seg) (cdr seg)) (define (make-point x y) (cons x y)) (define (x-point p) (car p)) (define (y-point p) (cdr p)) (define (midpoint-segment seg) (let ((a (start-segment seg)) (b (end-segment seg))) (make-point (/ (+ (x-point a) (x-point b)) 2) (/ (+ (y-point a) (y-point b)) 2)))) (define (print-point p) (newline) (display "(") (display (x-point p)) (display ",") (display (y-point p)) (display ")")) (print-point (midpoint-segment (make-segment (make-point 32 21) (make-point 45 10)))) ; exercise 2.3 ;; 假設矩形的邊平行於座標軸，然後用左下點+右上點確定一個矩形 (define (make-rect left-bottom right-top) (cons left-bottom right-top)) (define (left-bottom rect) (car rect)) (define (right-top rect) (cdr rect)) (define (width-rect rect) (- (x-point (right-top rect)) (x-point (left-bottom rect)))) (define (height-rect rect) (- (y-point (right-top rect)) (y-point (left-bottom rect)))) (define (perimeter-rect rect) (* (+ (width-rect rect) (height-rect rect)) 2)) (define (area-rect rect) (* (width-rect rect) (height-rect rect))) (define r (make-rect (make-point 1 2) (make-point 3 6))) (perimeter-rect r) (area-rect r) ;; 其他定義一個矩形方法有很多，例如左下點+長寬等 ; exercise 2.4 (define (cdr z) (z (lambda (p q) q)))
ex2.5
#lang racket ; exercise 2.5 (define (cons a b) (* (pow 2 a) (pow 3 b))) (define (car x) (f x 2)) (define (cdr x) (f x 3)) (define (pow base exp) (define (iter cur res) (if (= 0 cur) res (iter (- cur 1) (* base res)))) (iter exp 1)) (define (f x base) (define (iter res) (if (= 0 (remainder x (pow base res))) (iter (+ res 1)) (- res 1))) (iter 1)) (define x (cons 4 6)) (car x) (cdr x)
ex2.6
這題是關於Church計數，首先我們來看一下維基百科上的定義：
---------------------------------我-----------是--------分---------割----------線----------------------------------------------
- 0 ≡
λf.λx. x - 1 ≡
λf.λx. f x - 2 ≡
λf.λx. f (f x) - 3 ≡
λf.λx. f (f (f x)) - ...
- n ≡
λf.λx. fn x - ...
就是說，自然數 
被表示為 Church 數n，它對於任何 lambda-項
F 和 X 有著性質：
- n
F X=βFn X。
---------------------------------我-----------是--------分---------割----------線----------------------------------------------
按照我的理解是：0代表函式f在變數x上作用0次，1代表函式f在變數x上作用1次，... ... ，n代表函式f在變數x上作用n次；其中函式f和變數x是使用者自己定義的。上述等式左邊代表特殊的0~n（其實他們是函式，需要知道f,
x才能求值，也就是需要傳入2個引數）
例如我們可以定義x=0，f(x)=x+1，那麼等式左邊的0~n求值後就對應自然數中的0~n
另外Church計數還定義瞭如下操作：
---------------------------------我-----------是--------分---------割----------線----------------------------------------------
加法函式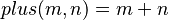 
利用了恆等式
。
- plus ≡
λm.λn.λf.λx. m f (n f x)
後繼函式 
β-等價於
(plus 1)。
- succ ≡
λn.λf.λx. f (n f x)
乘法函式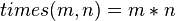 
利用了恆等式
。
- mult ≡
λm.λn.λf. n (m f)
指數函式 
由 Church 數定義直接給出。
- exp ≡
λm.λn. n m
有了上面這些知識，這題就比較容易理解了。這題給出了0和後繼函式succ的定義，讓我們求1,2, plus的定義。
已知0和後繼函式succ的定義：
(define zero (lambda (f) (lambda (x) x)))
(define (add-1 n) ;;
(lambda (f) (lambda (x) (f ((n f) x)))))例如我們可以進行如下的呼叫((zero f) 100)，其中f可以為任意函式，那麼這個表示式的值為100
根據上面的2個定義，我們可以進行如下推到：
one
= add-1 zero
= lambda (f) (lambda (x) (f ((zero f) x)))
= lambda (f) (lambda (x) (f ((lambda (x) x) x)))
= lambda (f) (lambda (x) (f x))
因而one定義如下：
(define one (lambda (f) (lambda (x) (f x))))= add-1 one
= lambda (f) (lambda (x) (f ((one f) x)))
= lambda (f) (lambda (x) (f ((lambda (x) (f x)) x)))
= lambda (f) (lambda (x) (f (f x)))
因而two定義如下：
(define two (lambda (f) (lambda (x) (f (f x)))))從而我們可以推出n的定義：
(define n (lambda (f) (lambda (x) (f (f ... f (x))))))我們在使用n這個函式的時候可以這樣呼叫：((n f) x)，其中f, x可以由使用者定義，它的值就是f(...f(x)...)
下面我們來解決加法問題。
(add m n)可以認為對變數n呼叫了m次add-1函式
呼叫1次add-1：
(lambda (f) (lambda (x) (f ((n f) x))))即
(lambda (f) (lambda (x) ((one f) ((n f) x))))呼叫2次add-1：
(lambda (f) (lambda (x) (f (f((n f) x)))))(lambda (f) (lambda (x) ((two f) ((n f) x))))....
呼叫m次add-1：
(lambda (f) (lambda (x) (f...((n f) x))))(lambda (f) (lambda (x) ((m f) ((n f) x))))(define (add m n)
(lambda (f) (lambda (x) ((m f) ((n f) x)))))