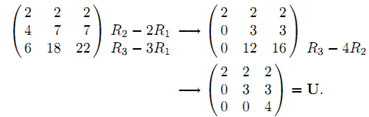1.三角分解(LU分解)

矩陣的LU分解是將一個矩陣分解為一個下三角矩陣與上三角矩陣的乘積。本質上，LU分解是高斯消元的一種表達方式。首先，對矩陣A通過初等行變換將其變為一個上三角矩陣。對於學習過線性代數的同學來說，這個過程應該很熟悉，線性代數考試中求行列式求逆一般都是通過這種方式來求解。然後，將原始矩陣A變為上三角矩陣的過程，對應的變換矩陣為一個下三角矩陣。這中間的過程，就是Doolittle algorithm(杜爾裡特演算法)。

轉一個Tony Ma同學寫的例子：
若AX=b是一個非奇異系統，那麼高斯消元法將A化簡為一個上三角矩陣。若主軸上沒有0值，則無需互動行，因此只需進行第3類初等行變換（把第 i 行加上第 j 的 k 倍）即可完成此變換。例如

第3類行變換可以通過左乘相應的初等矩陣image實現，對上例來說進行的3個變換就是相應初等矩陣的乘積。注意最右邊是一個下三角矩陣L

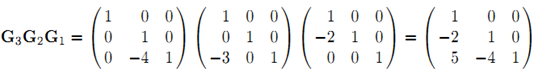
從而有G3G2G1A=U，即A=G−11G−12G−13U。因此A=LU，為一個下三角與一個上三角矩陣的乘積，因此稱為LU分解。
注意:
1）U是高斯消元的結果，且對角線上是主元
2）L對角線上是1，對角線下面的元素image恰恰是在式1中用於消去（i,j）位置上元素的乘子。

LU分解常用來求解線性方程組，求逆矩陣或者計算行列式。例如在計算行列式的時候，A=LU，det(A)=det(L)det(U)。而對於三角矩陣來說，行列式的值即為對角線上元素的乘積。所以如果對矩陣進行三角分解以後再求行列式，就會變得非常容易。

線上性代數中已經證明，如果方陣A是非奇異的，即A的行列式不為0，LU分解總是存在的。

2.QR分解

QR分解是將矩陣分解為一個正交矩陣與上三角矩陣的乘積。用一張圖可以形象地表示QR分解：

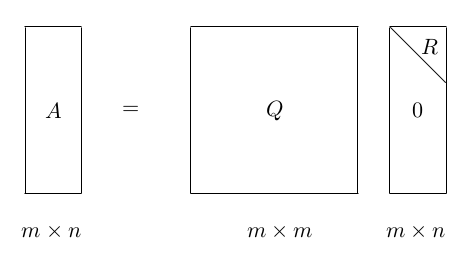
這其中， Q為正交矩陣，QTQ=I，R為上三角矩陣。
實際中，QR分解經常被用來解線性最小二乘問題。

3.Jordan分解

每次看到Jordan分解，就想起當年考研的那段時光。控制原理裡面，就有大段關於Jordan分解的內容。可惜當時矩陣分析沒有學到位，線性代數裡頭又沒有提到Jordan分解，所以理解起來那個費勁。
廢話這麼多，先來看看Jordan到底是個什麼鬼：
我們將下面的k

×k階方陣

JK(λ)=⎡⎣⎢⎢⎢⎢⎢⎢λ1λ1⋱⋱λ1λ⎤⎦⎥⎥⎥⎥⎥⎥k×k
稱為Jordan塊。同時，我們也將由若干個Jordan塊組成的對角矩陣成為Jordan陣。
由Jordan塊的定義不難看出，Jordan 陣與對角陣的差別僅在於它的上 (下)對角線的元素是0或1。因此，它是特殊的上三角陣。

為什麼要進行Jordan分解呢？或者說，Jordan分解能解決什麼問題呢？
我們先來複習一下，如果一個n階方陣A可以對角化，那麼A至少滿足下列條件的一個：
1.A有n個線性無關的特徵向量。
2.A的所有特徵值的幾何重數等於相應的代數重數，即qi=pi。
3.A的極小多項式經標準分解後，每一項都是一次項，且重數都是1。

因為有的矩陣不可以進行對角化，那麼我們可以對它進行Jordan分解，達到簡化計算的目的。

4.SVD分解