分類： 機器學習2013-07-24 11:50 517人閱讀 評論(5) 收藏 舉報

目錄(?)[-]

==========================================================================================

最近一直在看Deep Learning，各類部落格、論文看得不少

但是說實話，這樣做有些疏於實現，一來呢自己的電腦也不是很好，二來呢我目前也沒能力自己去寫一個toolbox

只是跟著Andrew Ng的UFLDL tutorial 寫了些已有框架的程式碼(這部分的程式碼見github)

後來發現了一個matlab的Deep Learning的

再一個就是matlab的實現可以省略掉很多資料結構的程式碼，使演算法思路非常清晰

所以我想在解讀這個toolbox的程式碼的同時來鞏固自己學到的，同時也為下一步的實踐打好基礎

(本文只是從程式碼的角度解讀演算法，具體的演算法理論步驟還是需要去看paper的

我會在文中給出一些相關的paper的名字，本文旨在梳理一下演算法過程，不會深究演算法原理和公式)

==========================================================================================

使用的程式碼：DeepLearnToolbox  ，下載地址：點選開啟，感謝該toolbox的作者

==========================================================================================

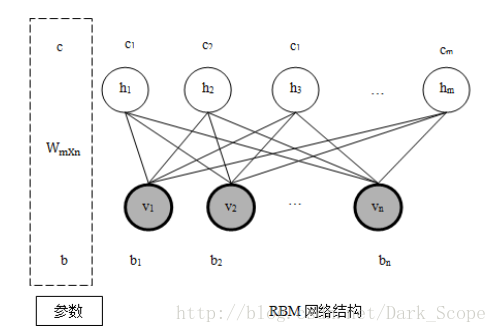
今天介紹DBN的內容，其中關鍵部分都是(Restricted Boltzmann Machines, RBM)的步驟，所以先放一張rbm的結構，幫助理解

(圖來自baidu的一個講解ppt)

==========================================================================================

照例，我們首先來看一個完整的DBN的例子程式：

這是\tests\test_example_DBN.m 中的ex2

1. //train dbn
2. dbn.sizes = [100 100];  
3. opts.numepochs =   1;  
4. opts.batchsize = 100;  
5. opts.momentum  =   0;  
6. opts.alpha     =   1;  
7. dbn =dbnsetup(dbn, train_x, opts);                //here！！！
8. dbn = dbntrain(dbn, train_x, opts);                //here！！！
9. //unfold dbn to nn
10. nn = dbnunfoldtonn(dbn, 10);                       //here！！！
11. nn.activation_function = 'sigm';  
12. //train nn
13. opts.numepochs =  1;  
14. opts.batchsize = 100;  
15. nn = nntrain(nn, train_x, train_y, opts);  
16. [er, bad] = nntest(nn, test_x, test_y);  
17. assert(er < 0.10, 'Too big error'); 

其中的過程簡單清晰明瞭，就是dbnsetup(),dbntrain()以及dbnunfoldtonn()三個函式

最後fine tuning的時候用了（一）裡看過的nntrain和nntest，參見（一）

\DBN\dbnsetup.m

     這個實在沒什麼好說的，

     直接分層初始化每一層的rbm(受限波爾茲曼機(Restricted Boltzmann Machines, RBM))
     同樣，W,b,c是引數，vW,vb,vc是更新時用到的與momentum的變數，見到程式碼時再說

1. for u = 1 : numel(dbn.sizes) - 1  
2.     dbn.rbm{u}.alpha    = opts.alpha;  
3.     dbn.rbm{u}.momentum = opts.momentum;  
4.     dbn.rbm{u}.W  = zeros(dbn.sizes(u + 1), dbn.sizes(u));  
5.     dbn.rbm{u}.vW = zeros(dbn.sizes(u + 1), dbn.sizes(u));  
6.     dbn.rbm{u}.b  = zeros(dbn.sizes(u), 1);  
7.     dbn.rbm{u}.vb = zeros(dbn.sizes(u), 1);  
8.     dbn.rbm{u}.c  = zeros(dbn.sizes(u + 1), 1);  
9.     dbn.rbm{u}.vc = zeros(dbn.sizes(u + 1), 1);  
10. end 

\DBN\dbntrain.m

     應為DBN基本就是把rbm當做磚塊搭建起來的，所以train也很簡單

1. function dbn = dbntrain(dbn, x, opts)  
2.     n = numel(dbn.rbm);  
3. //對每一層的rbm進行訓練
4.     dbn.rbm{1} = rbmtrain(dbn.rbm{1}, x, opts);  
5. for i = 2 : n  
6.         x = rbmup(dbn.rbm{i - 1}, x);  
7.         dbn.rbm{i} = rbmtrain(dbn.rbm{i}, x, opts);   
8.     end  
9. end 

  首先映入眼簾的是對第一層進行rbmtrain()，後面每一層在train之前用了rbmup，

  rbmup其實就是簡單的一句sigm(repmat(rbm.c', size(x, 1), 1) + x * rbm.W');

  也就是上面那張圖從v到h計算一次，公式是Wx+c

   接下來是最關鍵的rbmtrain了：

\DBN\rbmtrain.m

        程式碼如下，說明都在註釋裡

         論文參考：【1】Learning Deep Architectures for AI   以及   

                          【2】A Practical Guide to Training Restricted Boltzmann Machines

         你可以和【1】裡面的這段虛擬碼對應一下

1. for i = 1 : opts.numepochs //迭代次數
2.      kk = randperm(m);  
3.      err = 0;  
4. for l = 1 : numbatches  
5.          batch = x(kk((l - 1) * opts.batchsize + 1 : l * opts.batchsize), :);  
6.          v1 = batch;  
7.          h1 = sigmrnd(repmat(rbm.c', opts.batchsize, 1) + v1 * rbm.W');            //gibbs sampling的過程
8.          v2 = sigmrnd(repmat(rbm.b', opts.batchsize, 1) + h1 * rbm.W);  
9.          h2 = sigmrnd(repmat(rbm.c', opts.batchsize, 1) + v2 * rbm.W');  
10. //Contrastive Divergence 的過程 
11. //這和《Learning Deep Architectures for AI》裡面寫cd-1的那段pseudo code是一樣的
12.          c1 = h1' * v1;  
13.          c2 = h2' * v2;  
14. //關於momentum，請參看Hinton的《A Practical Guide to Training Restricted Boltzmann Machines》
15. //它的作用是記錄下以前的更新方向，並與現在的方向結合下，跟有可能加快學習的速度
16.          rbm.vW = rbm.momentum * rbm.vW + rbm.alpha * (c1 - c2)     / opts.batchsize;      
17.          rbm.vb = rbm.momentum * rbm.vb + rbm.alpha * sum(v1 - v2)' / opts.batchsize;  
18.          rbm.vc = rbm.momentum * rbm.vc + rbm.alpha * sum(h1 - h2)' / opts.batchsize;  
19. //更新值
20.          rbm.W = rbm.W + rbm.vW;  
21.          rbm.b = rbm.b + rbm.vb;  
22.          rbm.c = rbm.c + rbm.vc;  
23.          err = err + sum(sum((v1 - v2) .^ 2)) / opts.batchsize;  
24.      end  
25. end 

\DBN\dbnunfoldtonn.m

      DBN的每一層訓練完成後自然還要把引數傳遞給一個大的NN，這就是這個函式的作用

1. function nn = dbnunfoldtonn(dbn, outputsize)  
2. %DBNUNFOLDTONN Unfolds a DBN to a NN  
3. %   outputsize是你的目標輸出label，比如在MINST就是10，DBN只負責學習feature  
4. %   或者說初始化Weight，是一個unsupervised learning，最後的supervised還得靠NN  
5. if(exist('outputsize','var'))  
6.         size = [dbn.sizes outputsize];  
7. else
8.         size = [dbn.sizes];  
9.     end  
10.     nn = nnsetup(size);  
11.     %把每一層展開後的Weight拿去初始化NN的Weight  
12.     %注意dbn.rbm{i}.c拿去初始化了bias項的值  
13. for i = 1 : numel(dbn.rbm)  
14.         nn.W{i} = [dbn.rbm{i}.c dbn.rbm{i}.W];  
15.     end  
16. end 

最後fine tuning就再訓練一下NN就可以了

總結

      還是那句話，本文只是梳理一下學習路線，具體的東西還是要靠paper

      dbn主要的關鍵就是rbm，推薦幾篇經典的文章吧，rbm可是Hinton的寶貝啊

      其中涉及到MCMC，Contrastive divergence，感覺比Autoencoder難理解多了

          [1] An Introduction to Restricted Boltzmann Machines

          [2] Learning Deep Architectures for AI                                                     Bengio大作啊

          [3] A Practical Guide to Training Restricted Boltzmann Machines              上面提到過，比較細緻

          [4] A learning Algorithm for Boltzmann Machines                                      Hinton的