《資料結構(C語言版)》- 樹和二叉樹
本文將討論非線性資料結構中的樹型結構。樹型結構中樹和二叉樹最常用,直觀來說,樹是以分支關係定義的層次結構,樹結構在客觀世界中廣泛存在,如人類社會的族譜,最上面是族長,然後下面依次是族長的孩子,孫子等等。這就可以用樹來更加形象的表示。樹在計算機領域中也有十分廣泛地應用,如在編譯程式中,可用樹來表示源程式的語法結構。
1. 樹的定義
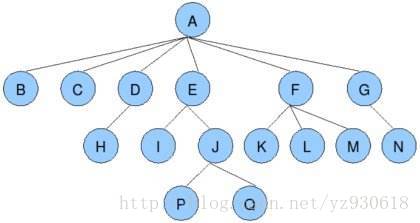
樹的形狀如下圖:
樹(Tree)是n(
有且僅有一個特定的稱為根(Root)的結點,如圖中的結點A就是這棵樹的根節點;
當
n>1 時,其餘結點可分為m(m>0 )個互不相交的有限集T1,T2,..., ,其中每一個集合又可以作為一棵樹,並稱為根的子樹(SubTree);Tm
2. 樹結構中的基本術語
下面將列出樹結構中的一些基本術語:
樹的結點所擁有的子樹的個數稱為結點的度(Degree)。如上圖中,A的度為6,D的度為1,P的度為0;
度為0的結點稱為葉子(Leaf)或終端結點。 如上圖中,B,C,H,I,P,Q,K,L,M,N都是葉子結點;
樹的度是樹內各結點的度的最大值。如上圖中,樹的度為4;
結點的子樹的根稱為該結點的孩子(Child),該結點同樣稱為孩子的雙親(Parent)。如上圖中,E為A的子樹的根,則E為A的孩子,而A則是E的雙親;
同一個雙親的孩子之間互稱兄弟(Sibling)。如上圖中,B,C,D,E,F,G互為兄弟;
結點的祖先是從根到該結點所經過分支上的所有結點。反之,以某結點為根的子樹中的任一結點都稱為該結點的子孫。如上圖中,P的祖先為A,E,J,E的子孫為I,J,P,Q;
結點的層次(Level)從根開始定義起,根為第一層,根的孩子為第二層,以此類推。
結點雙親都在同一層的結點互為堂兄弟。如上圖中,H,I,J,K,L,M,N互為堂兄弟。
樹中結點的最大層次稱為樹的深度(Depth)或高度。如上圖中,樹的深度為4;
如果將樹中結點的各子樹看成從左至右是有次序的(即不能互換),則稱該樹為有序樹,否則稱為無序樹。如上圖中,如果將A的以D為根的子樹和以E為根的子樹互換位置後和原先的樹表示兩顆樹,則稱該樹為有序樹,如果表示同一棵樹,則稱該樹為無序樹。在有序樹中最左邊的子樹的根稱為第一個孩子,最右邊的稱為最後一個孩子;
森林(Forest)是m(
m≥0 )棵互不相交的樹的集合。
3. 二叉樹的定義
二叉樹(Binary Tree)是另一種樹型結構,它的特點是每個結點至多只有兩顆子樹,也就是說,二叉樹不存在度大於2的結點,並且二叉樹的子樹有左右之分,其次序不能任意顛倒。
一顆深度為
如果對滿二叉樹的結點進行連續編號,約定遍號從根節點起,自上而下,自左至右。其中,深度為
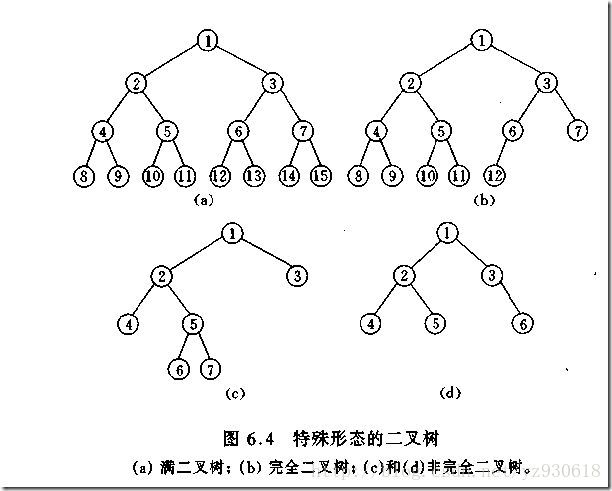
如下圖,(a)和(b)分別為完成二叉樹和滿二叉樹,而(c)和(d)為非完成二叉樹:
抽象資料型別二叉樹的定義如下:


4. 二叉樹的性質
下面敘述二叉樹的重要性質:
性質1 : 在二叉樹的第
i 層上至多有2i−1 個結點(i≥1 )。性質2 : 深度為
k 的二叉樹至多有2k−1 個結點(k≥1 )。性質3 :對任何一顆二叉樹
T ,如果其葉子結點數為n0 ,度為2的結點數為n2 ,則n0=n2+1 。性質4 :具有
n 個結點的完全二叉樹的深度為[log2n]+1 。性質5:如果對一顆有
n 個結點的完全二叉樹的結點按層序編號,則對任一結點i(1≤i≤n) ,有:(1) 如果
i=1 ,則結點i 是二叉樹的根,無雙親;如果i>1 ,則其雙親是結點[i/2] 。(2) 如果
2i>n ,則結點i 無左孩子(由於是完全二叉樹,所以結點i 是葉子結點);否則其左孩子是結點2i 。(3) 如果
2i+1>n ,則結點i 無右孩子;否則其右孩子是結點2i+1 。
5. 二叉樹的Java實現
下面是二叉樹的Java實現:
二叉樹結構類:
/**
* Created by yuzhan on 2017/8/24.
*/
public class TreeNode<T> {
public T val; //結點值
public TreeNode<T> left; //左結點的值
public TreeNode<T> right; //右結點的值
public TreeNode(T data){
this.val = data;
this.left = null;
this.right = null;
}
public TreeNode(){
}
}二叉樹方法介面
/**
* 二叉樹介面
* Created by yuzhan on 2017/8/24.
*/
public interface BinaryTree<T> {
/**
* 構造空二叉樹
*/
TreeNode InitBiTree();
/**
* 銷燬二叉樹
*/
void DestroyBiTree(TreeNode tree);
/**
* 按Object[]構造二叉樹
*/
TreeNode CreateBiTree(Object[] array);
/**
* 將二叉樹清為空樹
*/
void ClearBiTree(TreeNode tree);
/**
* 若二叉樹存在,則返回TRUE,否則FALSE
*/
Boolean BiTreeEmpty(TreeNode tree);
/**
* 返回二叉樹的根
* @return
*/
T Root(TreeNode tree);
/**
* 先序遍歷
*/
void preOrderByRecurse(TreeNode node);
/**
* 中序遍歷
*/
void InOrderByRecurse(TreeNode root);
/**
* 後序遍歷
*/
public void PostOrderByRecurse(TreeNode root);
}二叉樹方法介面實現類
import java.util.ArrayList;
import java.util.List;
/**
* 二叉樹介面實現類
* Created by yuzhan on 2017/8/24.
*
*/
public class BinaryTreeImpl<T> implements BinaryTree<T>{
/**
* 構造空二叉樹T
*/
public TreeNode InitBiTree(){
return new TreeNode();
}
/**
* 銷燬二叉樹
*/
public void DestroyBiTree(TreeNode tree){
if(tree != null){
tree.val = null;
tree.left = null;
tree.right = null;
}else{
throw new IllegalArgumentException("二叉樹為空");
}
}
/**
* 按Object[]構造二叉樹
*/
public TreeNode CreateBiTree(Object[] array){
if(array == null || array.length == 0){
throw new IllegalArgumentException("輸入不合法");
}else{
//將Object存入list中
List<TreeNode<T>> list = new ArrayList<>();
for(int i = 0;i < array.length;i++){
list.add(new TreeNode<T>((T) array[i]));
}
//為結點賦值(由於是完全二叉樹構造方式,所以非葉子結點的數量為[n/2])
for(int j = 0;j < (list.size() /2);j++){
try {
//為左子樹賦值 2*j + 1
if((2*j + 1) < list.size())
list.get(j).left = list.get(2 * j + 1);
else
list.get(j).left = null;
//為右子樹賦值 2*j + 2
if((2*j + 2) < list.size())
list.get(j).right = list.get(2 * j + 2);
else
list.get(j).right = null;
} catch (Exception e) {
e.printStackTrace();
}
}
TreeNode tree = new TreeNode();
//為根結點賦值
tree.val = list.get(0).val;
//為根結點的左子樹賦值
if(list.get(0).left != null){
tree.left = list.get(0).left;
}else{
tree.left = null;
}
//為根結點的右子樹賦值
if(list.get(0).right != null){
tree.right = list.get(0).right;
}else{
tree.right = null;
}
return tree;
}
}
/**
* 將二叉樹清為空樹
*/
public void ClearBiTree(TreeNode tree){
if(tree.val != null){
tree.val = null;
tree.right = null;
tree.left = null;
}else{
throw new IllegalArgumentException("二叉樹為空");
}
}
/**
* 若二叉樹存在,則返回TRUE,否則FALSE
*/
public Boolean BiTreeEmpty(TreeNode tree){
if(tree.val != null){
return false;
}else{
return true;
}
}
/**
* 返回二叉樹的根
* @return
*/
public T Root(TreeNode tree){
if(tree.val != null){
return (T) tree.val;
}else{
throw new IllegalArgumentException("二叉樹為空");
}
}
/**
* 先序遍歷
*/
public void preOrderByRecurse(TreeNode root) {
if (root == null) {
return;
}
System.out.print(root.val+" ");
preOrderByRecurse(root.left);
preOrderByRecurse(root.right);
}
/**
* 中序遍歷
*/
public void InOrderByRecurse(TreeNode root) {
if (root == null) {
return;
}
InOrderByRecurse(root.left);
System.out.print(root.val+" ");
InOrderByRecurse(root.right);
}
/**
* 後序遍歷
*/
public void PostOrderByRecurse(TreeNode root) {
if (root == null) {
return;
}
PostOrderByRecurse(root.left);
PostOrderByRecurse(root.right);
System.out.print(root.val+" ");
}
}測試類
public static void main(String[] args) {
BinaryTree<Integer> bt = new BinaryTreeImpl<>();
TreeNode tree;
//tree = bt.InitBiTree(); // 初始化空二叉樹
//bt.DestroyBiTree(tree); //銷燬二叉樹
Object[] array = {1,2,3,4,5,6,7,8,9,10};
tree = bt.CreateBiTree(array); //構造二叉樹
//bt.ClearBiTree(); //清空二叉樹
Boolean flag = bt.BiTreeEmpty(tree);//判斷二叉樹是否存在
Integer root = bt.Root(tree); //返回二叉樹的根結點
bt.preOrderByRecurse(tree); //前序遍歷
System.out.println();
bt.InOrderByRecurse(tree); //中序遍歷
System.out.println();
bt.PostOrderByRecurse(tree); //後序遍歷
}