原文地址：http://blog.csdn.net/jsqfengbao/article/details/47291207

題目：輸入一顆二叉樹和一個整數，打印出二叉樹中結點值的和為輸入整數的所有路徑。從樹的根節點開始往下一直到葉結點所經過的所有的結點形成一條路徑。

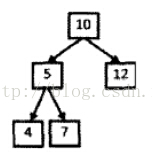
如下圖，輸入二叉樹和整數22，則打印出兩條路徑，第一條路徑包含結點10，12，第二條路徑包含的結點為10，5，7.

一般的資料結構和演算法的教材都沒有介紹樹的路徑，因此對大多數應聘者而言，這是一個新概念，也就很難一下子想出完整的解題思路。這個時候我們可以試著從一兩個具體的例子入手，找到規律。

以圖中的二叉樹為例分析，由於路徑是從根節點出發到葉結點，也就是說路徑是以根節點為起始點，因此我們首先需要遍歷根節點。在樹的前序、中序、後序三種遍歷方式中，只有前序遍歷是首先訪問根節點的。

按照前序遍歷的順序遍歷途中的二叉樹，在訪問結點10之後，就會訪問結點5.從二叉樹結點的定義可以看出，在本題的二叉樹結點中沒有指向父節點的指標，訪問到結點5的時候，我們是不知道前面經過了哪些結點的，除非我們把經過的路徑上的結點都儲存起來。每訪問到一個結點的時候，我們都把當前的結點新增到路徑中去。到達結點5時，路徑中包含兩個結點，他們的值分別是10和5.接下來遍歷到結點4，我們把這個結點也新增到路徑中，這個時候已經到達了葉結點，但路徑上三個結點的值之和為19.這個和不等於輸入的值22，因此不符合要求的路徑。

我們接著要遍歷其他的結點。在遍歷下一個節點之前，先要從結點4回到結點5，再去遍歷結點5的右子節點7.值得注意的是，回到結點5的時候，由於結點4已經不在前往結點7的路徑上了，我們需要把結點4從路徑中刪除。接下來訪問到結點7的時候，再把結點新增到路徑中。此時路徑中三個結點10，5，7之和剛好是22，是一條符合要求的路徑。

我們最後要遍歷的結點是12。在遍歷這個結點之前，需要先經過結點5回到結點10。同樣，每一次當從子節點回到父節點的時候，我們都需要在路徑上刪除子節點。最後從結點10到達結點12的時候，路徑上的兩個結點的值之和也是22，因此這也是一條符合條件的路徑。

總結過程如下：

分析完前面的具體的例子之後，我們就找到了一些規律。當用前序遍歷的方式訪問到某一節點時，我們把該結點新增到路徑上，並累加該結點的值。如果該結點為葉結點並且路徑中結點值的和剛好為輸入的整數，則當前的路徑符合要求，我們把它打印出來。如果當前的結點不是葉結點，則繼續訪問它的子節點。當前結點訪問結束後，遞迴函式將自動回到它的父節點。因此我們在函式退出之前要在路徑上刪除當前結點並減去當前結點的值，以確保返回父節點時路徑剛好是從根節點到父節點的路徑。我們不難看出儲存路徑的資料結構實際上是一個棧，因此路徑要與遞迴呼叫狀態一致，而遞迴呼叫的本質上是一個壓棧和出棧的過程。

用Java程式碼實現：

1. /** 
2.  * 輸入一顆二叉樹和一個整數，打印出二叉樹中結點值的和為輸入整數的所有路徑。從樹的根節點開始往下一直到葉結點所經過的結點形成一條路徑。 
3.  */
4. package swordForOffer;  
5. import java.util.Stack;  
6. import utils.BinaryTreeNode;  
7. /** 
8.  * @author JInShuangQi 
9.  * 
10.  * 2015年8月5日 
11.  */
12. publicclass E25PathInTree {  
13.     publicvoid findPath(BinaryTreeNode root,int k){  
14.         if(root == null)  
15.             return;  
16.         Stack<Integer> stack = new Stack<Integer>();  
17.         findPath(root,k,stack);  
18.     }  
19.     publicvoid findPath(BinaryTreeNode root,int k,Stack<Integer> path){  
20.         if(root == null)  
21.             return;  
22.         if(root.leftNode == null && root.rightNode == null){  
23.             if(root.value == k){  
24.                 System.out.println("路徑開始");  
25.                 for(int i :path){  
26.                     System.out.print(i+",");                                                                                             }  
27.                 System.out.print(root.value);  
28.             }  
29.         }  
30.         else{  
31.             path.push(root.value);  
32.             findPath(root.leftNode,k-root.value,path);  
33.             findPath(root.rightNode,k-root.value,path);  
34.             path.pop();  
35.         }  
36.     }  
37.     publicstaticvoid main(String[] args){  
38.         BinaryTreeNode root1 = new BinaryTreeNode();  
39.         BinaryTreeNode node1 = new BinaryTreeNode();  
40.         BinaryTreeNode node2 = new BinaryTreeNode();  
41.         BinaryTreeNode node3 = new BinaryTreeNode();  
42.         BinaryTreeNode node4 = new BinaryTreeNode();  
43.         BinaryTreeNode node5 = new BinaryTreeNode();  
44.         BinaryTreeNode node6 = new BinaryTreeNode();  
45.         root1.leftNode = node1;  
46.         root1.rightNode = node2;  
47.         node1.leftNode = node3;  
48.         node1.rightNode = node4;  
49.         node4.leftNode = node5;  
50.         node4.rightNode = node6;  
51.         root1.value = 8;  
52.         node1.value = 8;  
53.         node2.value = 7;  
54.         node3.value = 9;  
55.         node4.value = 2;  
56.         node5.value = 4;  
57.         node6.value = 7;  
58.         E25PathInTree test = new E25PathInTree();  
59.         test.findPath(root1, 25);  
60.     }  
61. }