原文自：https://www.cnblogs.com/chenyg32/p/3293247.html

一、問題描述

問題描述：N個人分配N項任務，一個人只能分配一項任務，一項任務只能分配給一個人，將一項任務分配給一個人是需要支付報酬，如何分配任務，保證支付的報酬總數最小。

問題數學描述：

二、例項分析---窮舉法

在講將匈牙利演算法解決任務問題之前，先分析幾個具體例項。

以3個工作人員和3項任務為例項，下圖為薪酬圖表和根據薪酬圖表所得的cost矩陣。

利用最簡單的方法(窮舉法)進行求解，計算出所有分配情況的總薪酬開銷，然後求最小值。

total_cost1 = 250 + 600 + 250 = 1100;  x00 = 1,x11 = 1,x22 = 1;

total_cost2 = 250 + 350 + 400 = 1000;  x00 = 1,x12 = 1,x21 = 1;

total_cost3 = 400 + 400 + 250 = 1050;  x01 = 1,x10 = 1,x22 = 1;

total_cost4 = 400 + 350 + 200 = 950;   x01 = 1,x12 = 1,x20 = 1;  //最優分配

total_cost5 = 350 + 400 + 400 = 1150; x02 = 1,x10 = 1,x21 = 1;

total_cost6 = 350 + 600 + 250 = 1150; x02 = 1,x11 = 1,x22 = 1;

對於任務數和人員數較少時，可利用窮舉法計算結果。

若將N任務分配給N個人員，其包含的所有分配情況數目為N!，N增大時，窮舉法將難以完成任務。

三、匈牙利演算法

下面簡要介紹匈牙利演算法。

其基本的理論基礎是針對cost矩陣，將cost矩陣的一行或一列資料加上或減去一個數，其最優任務分配求解問題不變。

演算法的基本步驟如下：

四、例項分析---匈牙利演算法

下面結合具體例項，分析匈牙利演算法如何解決任務分配問題。

以N = 4為例項，下圖為cost列表和cost矩陣。

Step1.從第1行減去75，第2行減去35，第3行減去90，第4行減去45。

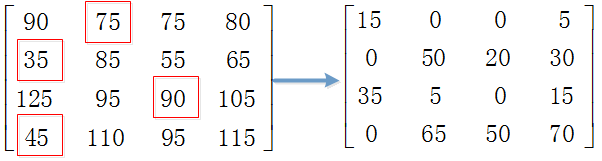
Step2.從第1列減去0，第2列減去0，第3列減去0，第4列減去5。

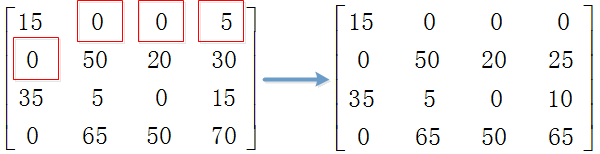
Step3.利用最少的水平線或垂直線覆蓋所有的0。

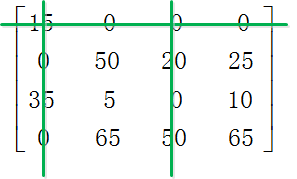
Step4.由於水平線和垂直線的總數是3，少於4，進入Step5。

Step5.沒有被覆蓋的最小值是5，沒有被覆蓋的每行減去最小值5，被覆蓋的每列加上最小值5，然後跳轉到步驟3.

Step3.利用最少的水平線或垂直線覆蓋所有的0。

Step4.由於水平線和垂直線的總數是3，少於4，進入Step5。

Step5.沒有被覆蓋的最小值是20，沒有被覆蓋的每行減去最小值20，被覆蓋的每列加上最小值20，然後跳轉到步驟3.

Step3.利用最少的水平線或垂直線覆蓋所有的0。

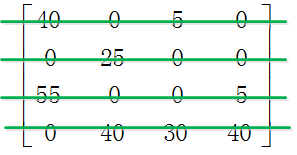
Step4.由於水平線和垂直線的總數是4，演算法結束，分配結果如下圖所示。

其中，黃色框表示分配結果，左邊矩陣的最優分配等價於左邊矩陣的最優分配。

五、參考資料

http://www.hungarianalgorithm.com/examplehungarianalgorithm.php
https://brilliant.org/wiki/hungarian-matching/