二叉樹相關程式設計題總結
關於二叉樹的五道面試題的總結
- 求二叉樹的最遠兩個結點的距離;
- 由前序遍歷和中序遍歷重建二叉樹;
- 判斷一棵樹是否是完全二叉樹;
- 求二叉樹兩個節點的最近公共祖先;
- 將二叉搜尋樹轉換成一個排序的雙向連結串列。要求不能建立任何新的結點,只能調整樹中結點指標的指向。
請仔細閱讀程式碼和註釋!!!
<一> 求二叉樹的最遠兩個結點的距離
本題在上一篇部落格中已經進行了詳細的實現,下面給出本題的連線:
<二>由前序遍歷和中序遍歷重建二叉樹
分析:這是一道考察基礎的題目,即對二叉樹的遍歷方式是否有深刻的瞭解,同時也考察對二叉樹的構建的瞭解,通常給定一個序列構建二叉樹的方式是利用前序遍歷並且結合非法值的方式進行構建,這個在第一題的實現中已經有了體現;
目前我們所瞭解的二叉樹的遍歷方式有四種:前,中,後,層序遍歷;
其中前序遍歷是深度優先遍歷,層序遍歷是廣度優先遍歷(這個會在第三題中用到);當然,這個屬於只是擴充套件;
本題所考察的前序和中序遍歷構建二叉樹,我們以下面這倆個序列為例,分析:
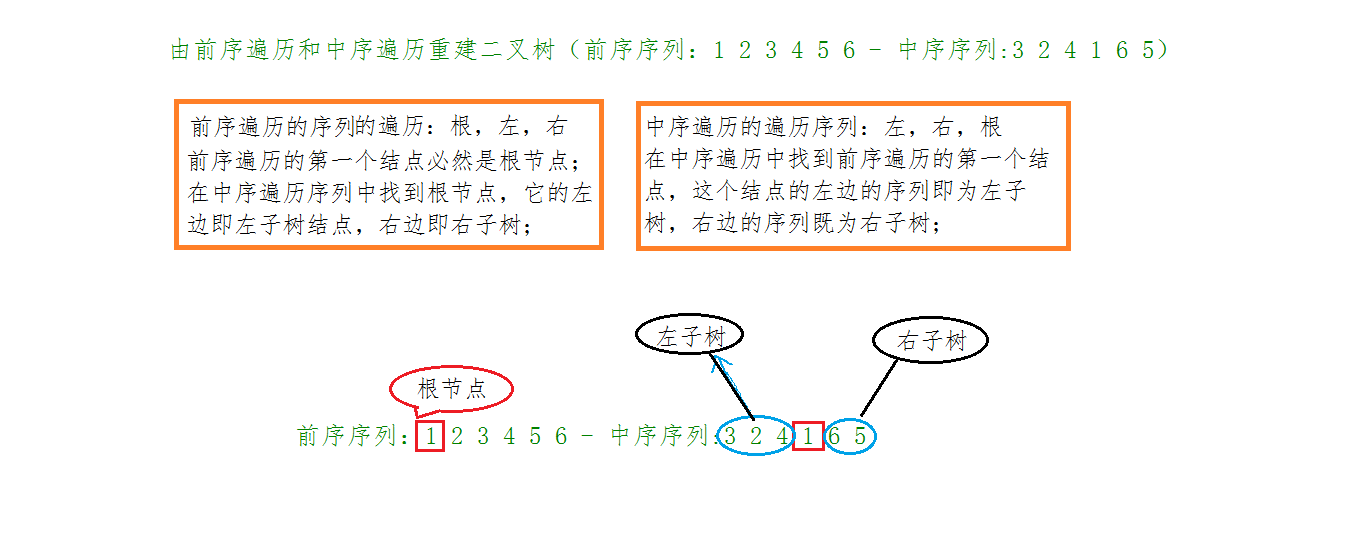
(前序序列:1 2 3 4 5 6 - 中序序列:3 2 4 1 6 5)
:我們根據前序和中序的特性,劃分出了根節點的左子樹和右子樹,那麼此時,我們至少知道了這棵樹的根節點,也就是擁有了根節點,還知道了左右子樹的節點個數,接下來,就該去建立它的左子樹和右子樹,而左右子樹又可以單獨的看作是一棵樹,我們可以知道左右子樹的根節點,怎麼知道的?
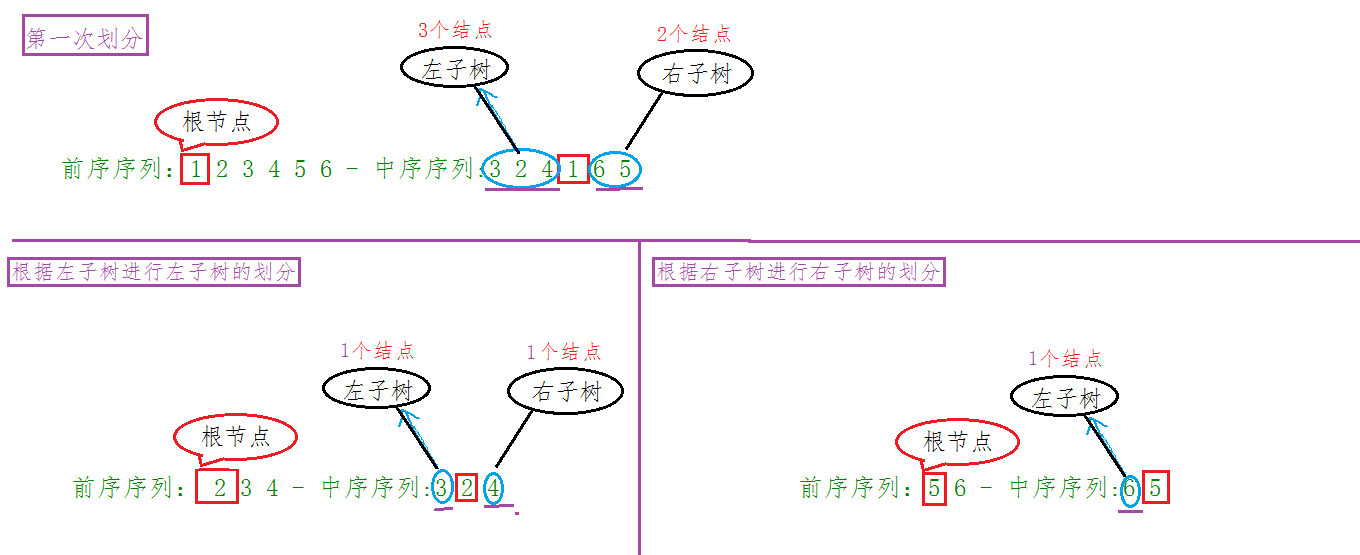
前序遍歷就在那放著,根結點1 的右邊第一個不就是左子樹的根節點,而根據中序遍歷我們又知道左子樹的節點個數,1 往右 3 個結點之後不就是5;那麼 5 就是 1 的右子樹的根節點,以此類推,這棵樹都所有結點我們都擁有了,樹不就建出來了,下面給出一個圖示:
:思路都理得差不多了,但是實現程式碼又和思路有些差異,因為程式碼的實現需要考慮很多因素,所以,請仔細看程式碼的實現;
程式碼:
//前序序列:1 2 3 4 5 6 - 中序序列:3 2 4 1 6 5
//在沒有重複節點的前提下
Node* _GreatTree(int* prestart, int* preend,int* inarrstart,int* inarrend)
{
Node* root = new Node(*prestart);
//如果只有當前一個節點,則將建立好的這個節點返回;
if(prestart == preend && inarrstart == inarrend)
return <三>判斷一棵樹是否是完全二叉樹
分析:這道題可以這麼說,如果你想到了方法,就很簡單不過了,沒有思路的話當然就不簡單了,當你不會的時候看了一下別人的解決方法,又會痛心疾首的痛恨自己怎麼這麼簡單的題都想不出來!
當然,以上純屬廢話;
判斷一顆樹是否是完全二叉樹,首先需要知道什麼是完全二叉樹,我相信有很多人對這個概念並不是很清晰;
完全二叉樹(Complete Binary Tree)
若設二叉樹的深度為h,除第 h 層外,其它各層 (1~h-1) 的結點數都達到最大個數,第 h 層所有的結點都連續集中在最左邊,這就是完全二叉樹。
完全二叉樹是由滿二叉樹而引出來的。對於深度為K的,有n個結點的二叉樹,當且僅當其每一個結點都與深度為K的滿二叉樹中編號從1至n的結點一一對應時稱之為完全二叉樹。
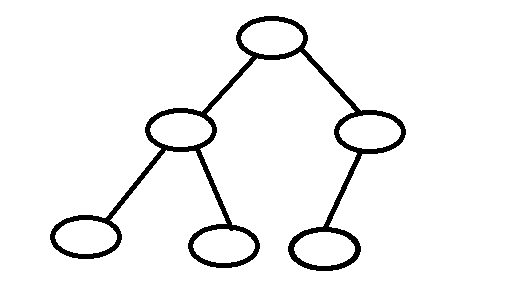
一棵二叉樹至多隻有最下面的一層上的結點的度數可以小於2,並且最下層上的結點都集中在該層最左邊的若干位置上,則此二叉樹成為完全二叉樹。
例如下面這棵樹:
那麼,瞭解了完全二叉樹的基本概念之後,這道題似乎就變得簡單了很多,既然前k-1層是滿二叉樹,而最後一層又是從左到右沒有間隔的,瞭解層序遍歷的同學相信很容易就想到了用層序遍歷來解這道題,至於什麼是層序遍歷,就不在這裡贅述了;
下面我給出這道題基於層序遍歷的兩種解法:
1)設定標誌法
從根節點開始,入佇列,如果佇列不為空,迴圈。
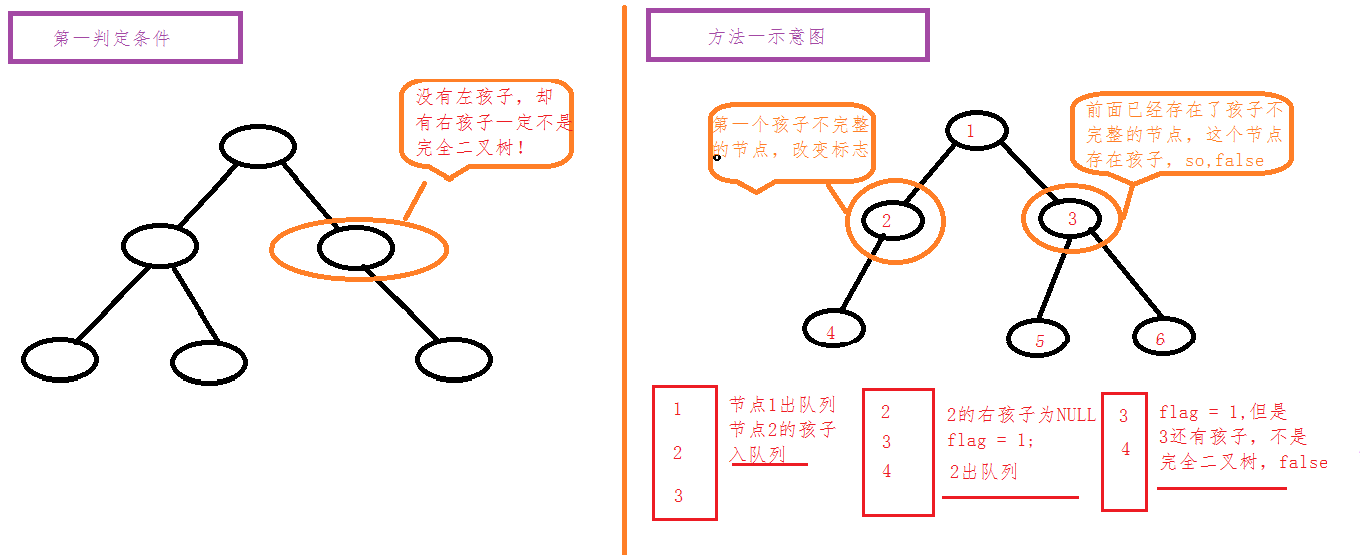
遇到第一個沒有左兒子或者右兒子的節點,設定標誌位,如果之後再遇到有左/右兒子的節點,那麼這不是一顆完全二叉樹。
圖示:
核心演算法程式碼實現:
bool IsCompleteTreeTwo(Node* root)
{
queue<Node*> q;
q.push(root);
Node* cur = q.front();
int flag = 0; //標誌
while(cur)
{
沒有左孩子卻有右孩子,一定不是完全二叉樹
if(cur->_left == NULL && cur->_right != NULL)
return false;
//如果flaga==1,並且當前節點右孩子,則false
if(flag == 1 && (cur->_left != NULL || cur->_right != NULL))
return false;
//當前節點沒有右孩子或者左孩子
if(cur->_left == NULL || cur->_right == NULL)
flag = 1;
if(cur->_left != NULL)
q.push(cur->_left);
if(cur->_right != NULL)
q.push(cur->_right);
q.pop();
if(!q.empty())
cur = q.front();
else
cur = NULL;
}
return true;
}2)剩餘佇列判空法
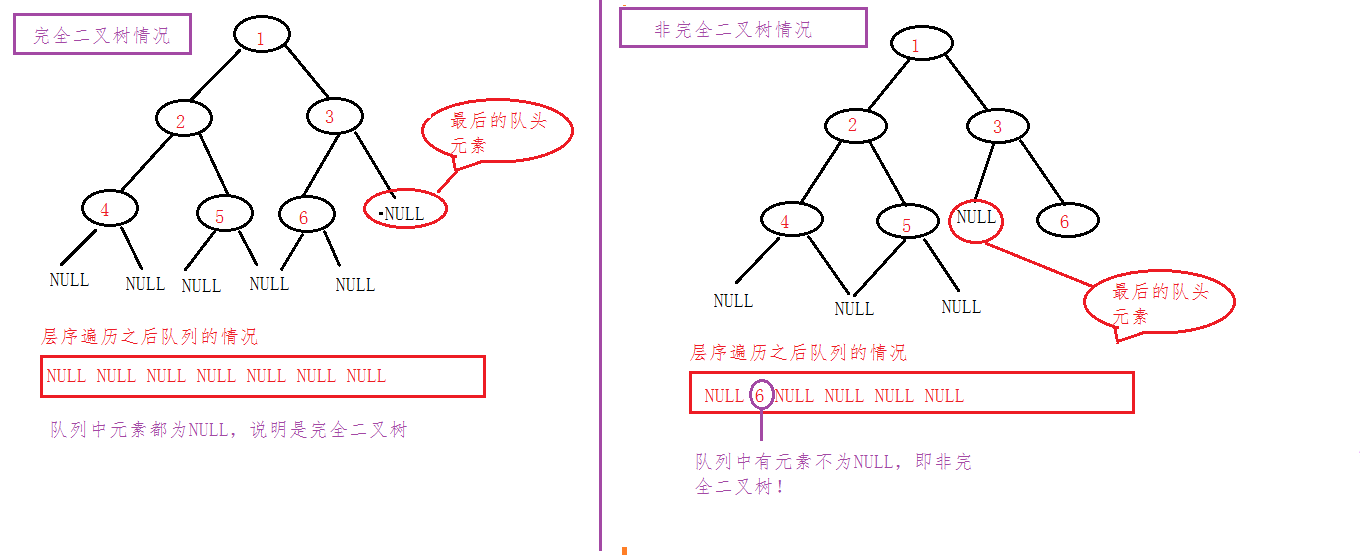
這個方法同樣需要入佇列,不同的在於判斷的方式,試想一顆完全二叉樹,我們把它的所有節點,包括葉子節點的左右空孩子都入佇列,通過層序遍歷,不斷的入佇列和出佇列的方式,如果遇到第一個隊頭元素為空,那麼如果是完全二叉樹的 話,此時一定遍歷完了所有節點,佇列中剩餘的元素肯定全是NULL的節點,也就是葉子節點的空孩子,如若不是如此,那麼,抱歉了,這就不是一顆完全二叉樹!
圖示:
圖中省略入隊出隊過程;
核心程式碼實現:
bool IsCompleteTree(Node* root)
{
if(root == NULL)
return false;
//用到輔助記憶體佇列
queue<Node*> q;
q.push(root);
//先將所有的節點以及它們的左右節點入佇列
Node* cur = q.front();
while(cur) //如果遇到第一個空節點停止
{
q.push(cur->_left);
q.push(cur->_right);
q.pop();
cur = q.front();
}
//此時應該是完全二叉樹的結尾;
//此時正確的情況應該是佇列中的所有元素都是NULL,否則不是完全二叉樹
while(!q.empty())
{
if(q.front() != NULL)
return false;
q.pop();
}
return true;
}本題完整程式碼實現連結:
<四>求二叉樹兩個節點的最近公共祖先
分析: 這道題是劍指offer上的一道題,難點在於全面的考慮各種情況,利用合適的方法解決各種情況;
什麼是最近公共祖先?
即從根節點分別到兩個節點的路經中最後一個公共節點,即最近公共祖先;
如下圖所示:
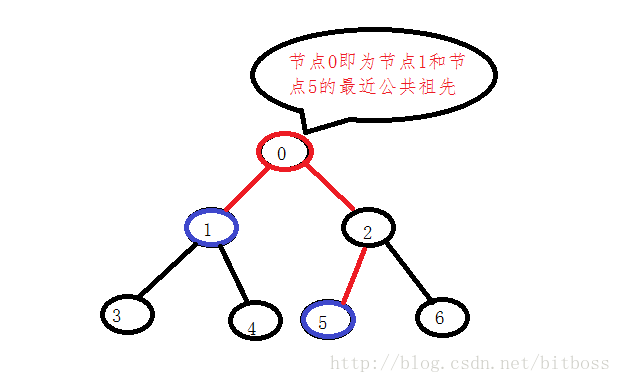
再然後,我們需要分析出都有哪些情況?
1)二叉搜尋樹
2)帶有父指標的二叉樹(就是三叉鏈)
3)一顆普通的樹
情況1:
最簡單的情景,即本身就是一顆二叉搜尋樹,即是有關聯的,那麼我們只要找到一個比其中一個節點大或者等於,並且比另一個節點小或者等於的節點就可以了,這個節點就是最低公共祖先,這個很好理解,就不多做贅述,直接上程式碼了;
//查詢最小公共祖先
int MinCommonAncestor(int x,int y)
{
Node* cur = _root;
Node* tmp = NULL;
while(cur)
{
//比兩個目標節點的值都大,繼續往左子樹找;
if(cur->_data > x && cur->_data > y)
{
tmp = cur;
cur = cur->_left;
}
//比兩個目標節點的值都小,繼續往右子樹找;
else if(cur->_data < x && cur->_data < y)
{
tmp = cur;
cur = cur->_right;
}
//符合條件找到目標節點
else if(cur->_data >= x && cur->_data <= y || cur->_data <= x && cur->_data >= y)
{
return cur->_data;
}
}
}情景2:
不是二叉搜尋樹,但是有父指標的二叉樹;
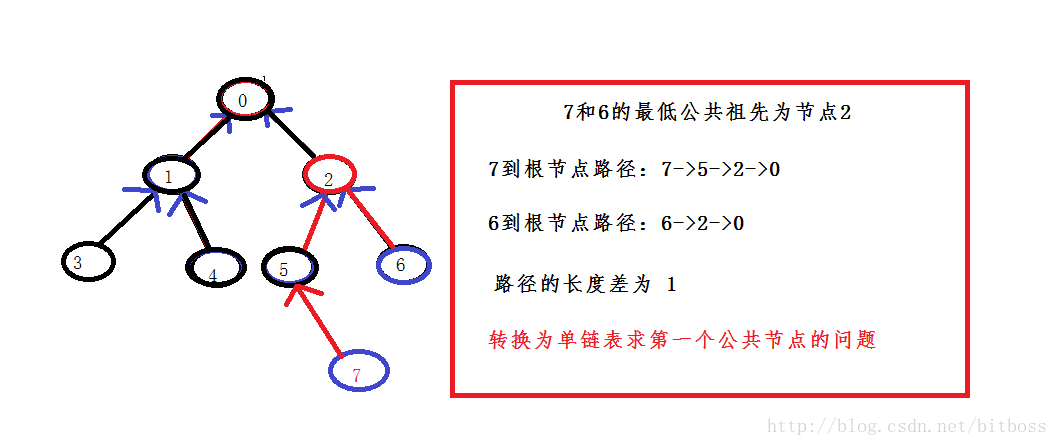
既然有父指標,即是三叉連,那麼問題就又變的簡單了,熟悉的同學應該很快就發現,這樣的話就把問題轉化為求兩條相交連結串列的第一個公共節點的問題了,當然,為什麼是第一個公共節點?前面說最低公共祖先的概念的時候不是說是從根節點分別到兩個節點的最後一個公共節點嗎?
不要急,你想想,現在我們有了父節點的話,完全可以從兩個目標節點往上遍歷,這不就是反著的了,求兩個相交節點的 第一個公共節點,出發點不一樣;
而從兩個目標節點向上遍歷的時候又有好幾種辦法,比如說利用棧,利用長度差的方法,棧的方法我們先不用,留到下一種情景用,這裡我們用的 是長度差的方法,何為長度差的方法?
長度差:即我們尋找兩個目標節點的時候,順便把從根節點到他們所經過的路徑長度儲存起來,分別是count1和count2; 然後求得他們的差值,即長的那條路徑比短的那條路徑多的節點數,為什麼要這樣呢?
因為我們需要逆向找路徑上的第一個公共節點,而如果從兩個目標節點同時出發的話,肯定就不是我麼想要的結果了,看著上面那個圖所舉得例子,如果7和6同時開始遍歷,那就有問題了,而如果我們讓路徑長的那個節點先走上他們的長度差的節點後,兩個節點再同時向上遍歷,第一個相同的節點不就是第一個公共節點了(當然,我們排除出現相同節點的可能性);
程式碼:
//查詢最小公共祖先
int MinCommonAncestor(int x,int y)
{
//根據已知節點向上查詢到根節點,求兩個連結串列的第一個交點
//前提都是建立在沒有重複元素的二叉樹中
if(x == y)
return x;
//不考慮返回空的情況,即暫時不考慮非法輸入
//採用找兩個連結串列第一個公共節點的方法求解,三種方法,窮舉,輔助棧,和求長度差;
//利用第三種方法,求長度差
int count1 = 1;
int count2 = 1;
Node* nodeone = NULL;
Node* nodetwo = NULL;
Node* cur = _root;
while(cur)
{
if(cur->_data == x)
{
nodeone = cur;
break;
}
++count1;
}
cur = _root;
while(cur)
{
if(cur->_data == y)
{
nodetwo = cur;
break;
}
++count2;
}
//求出長度差
int len = abs(count1 - count2);
if(count1 >= count2)
return _FindFirstNode(nodeone,nodetwo,len);
else
return _FindFirstNode(nodeone,nodetwo,len);
}
int _FindFirstNode(Node* one,Node* two, int len)
{
while(len--)
one = one->_parent;
while(one != two)
{
one = one->_parent;
two = two->_parent;
}
return one->_data;
}情景3:
普通的二叉樹,那就別無他法了,只能利用最原始的概念,從根節點開始分別到兩個目標節點的路徑的最後一個公共節點;
這樣的就沒有什麼技巧可言了,我們為了方便起見還是以二叉樹為例(當然,三叉,四岔的就麻煩點了);
可以利用兩種方法來實現:即遞迴和利用棧;
遞迴的思想有些類似於第一題的思想:利用遞迴帶返回值的方法進行判斷;
不停的向下遞迴,如果找到倆個目標節點的其中一個節點,就把當前這個節點返回,如果遞迴到葉子節點還沒有找到一個目標節點就返回NULL;
接收左右子樹的反饋結果,如果left和right都不為NULL,那麼很好,說明兩個目標節點分別在我的左右子樹上,返回當前節點,當前節點就是最低公共祖先;如果只有一顆子樹返回的非空值,那麼就說明兩個目標節點都在我的那個返回非空節點的子樹上,而返回值就是最低公共祖先,這裡是最難懂的地方,為什麼非空的返回值就是最低公共祖先?
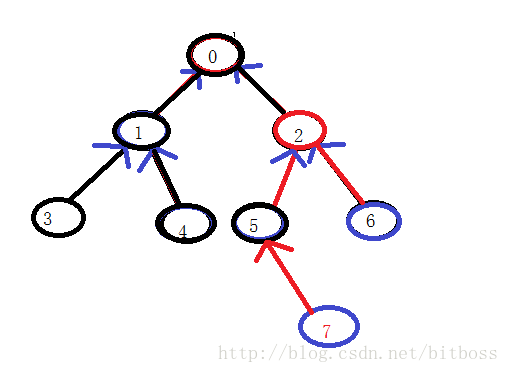
聯絡這張圖看看:
假如我們要求得2和5的最低公共祖先,那麼我們從根節點遞迴的往下遍歷,左子樹肯定是返回NULL了,而右子樹遞迴到2的時候就返回了,既然我已經找到了一個目標節點,那我就不繼續遞迴了,要不然另一個目標節點在另一個子樹上,不管我2的事,要不然5就在我2的子樹上,那就更簡單了,2就是最低公共祖先了,所以也就不存在很多同學擔心兩個目標節點在一條線上的情況會出現誤判的情況了;
講完這段感覺我都變2了;
int MinCommonAncestor(int x,int y)
{
Node* left = NULL;
Node* right = NULL;
Node* cur = _MinCommonAncestor(_root,x,y);
return cur->_data;
}
Node* _MinCommonAncestor(Node* root,const int x, const int y)
{
Node* left = NULL;
Node* right = NULL;
if(root == NULL)
return NULL;
if(root->_data == x || root->_data == y)
return root;
left = _MinCommonAncestor(root->_left,x,y);
right = _MinCommonAncestor(root->_right,x,y);
if(left && right)
return root;
return left ? left : right;
}利用棧的實現原理:無外乎就是儲存路徑,而棧的後進先出的特性,就又變成了第一個相同節點的問題了;
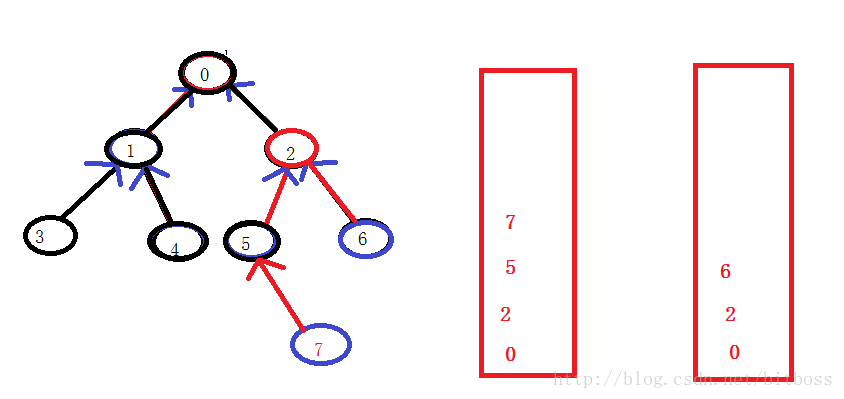
如圖:
7和6的路徑分別入棧,然後還是需要一個路徑差,不過這時候的路徑差就很簡單的可以利用棧的size()求出,同樣,size大的棧先pop掉路徑差個元素,然後,兩個棧同時pop,知道遇到一個相同的元素,這其實已經和情景2一樣了;
程式碼:
//利用遞迴和棧儲存路徑,然後消去兩條路徑的差值,進行同時pop();找到第一對不同;
int MinCommonAncestor(int x,int y)
{
stack<Node*> s1;
_MinCommonAncestor(_root,s1,x);
stack<Node*> s2;
_MinCommonAncestor(_root,s2,y);
if(s1.size() > s2.size())
{
int count = s1.size() - s2.size();
return FindCommonParent(s1,s2,count)->_data;
}
int count = s2.size() - s1.size();
return FindCommonParent(s2,s1,count)->_data;
}
Node* FindCommonParent(stack<Node*> first,stack<Node*> second,int count)
{
while(count--)
first.pop();
Node* cur = NULL;
while(!first.empty() && !second.empty() && first.top() != second.top())
{
first.pop();
second.pop();
}
return first.top();
}
bool _MinCommonAncestor(Node* root,stack<Node*>& s, const int x)
{
if(root == NULL)
return false;
if(root->_data == x)
{
s.push(root);
return true;
}
s.push(root);
bool left = _MinCommonAncestor(root->_left,s,x);
bool right = _MinCommonAncestor(root->_right,s,x);
if(left == false && right == false)
{
s.pop();
return false;
}
return true;
}<五>將二叉搜尋樹轉換成一個排序的雙向連結串列。要求不能建立任何新的結點,只能調整樹中結點指標的指向。
分析:怎麼說呢,這道題本質也很簡單,但是我們一看到限制條件就先慌張了,既然有附加條件肯定不會那麼簡單,那麼,其實想的複雜了,這道題其實就是簡單的考察你對二叉搜尋樹的瞭解;
二叉搜尋樹,也是有分別指向左子樹和右子樹的指標,而且中序遍歷有序;
而把二叉搜尋樹變為有序的雙向連結串列,第一點不免想到的肯定是中序遍歷的 方法,然後就是改變指標的指向,因為不允許建立新的節點,而改變指標的指向的話,就簡單很多了,只要讓left變為指向前一個節點的指標,right變為指向後一個節點的 指標就可以了,當然,程式碼的實現過程中肯定會有些許的細節差異!
程式碼:
Node* TurnToList()
{
Node* prev = NULL;
_TurnToList(_root,prev);
//返回雙向連結串列的頭結點
Node* cur = _root;
while(cur && cur->_left)
cur = cur->_left;
return cur;
}
void _TurnToList(Node* root, Node*& prev)
{
if(root == NULL)
return;
_TurnToList(root->_left,prev);
if(prev != NULL)
prev->_right = root;
prev = root;
_TurnToList(root->_right,prev);
}