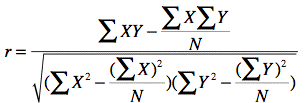利用matlab求三種相關係數
在多元分析中我們經常要用到相關係數。常用的相關係數有三種:Pearson相關係數,Kendall相關係數和Spearman相關係數。
一、Pearson相關係數
Pearson相關係數是英國統計學家皮爾遜於20世紀提出的一種計算直線相關的方法。
按照大學的線性數學水平來理解, 它比較複雜一點,可以看做是兩組資料的向量夾角的餘弦.
Pearson相關係數用來衡量兩個資料集合是否在一條線上面。其計算公式為:
一個具體的計算的例子:
X Y 1 2 2 5 3 6
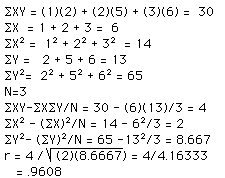
而利用matlab計算:函式 corrcoef
皮爾遜相關的約束條件
- 1 兩個變數間有線性關係
- 2 變數是連續變數
- 3 變數均符合正態分佈,且二元分佈也符合正態分佈
- 4 兩變數獨立
皮爾遜相關係數適用於:
(1)兩個變數之間是線性關係,都是連續資料。
(2)兩個變數的總體是正態分佈,或接近正態的單峰分佈。
(3)兩個變數的觀測值是成對的,每對觀測值之間相互獨立。
二、Kendall相關係數
Kendall相關係數是以Maurice Kendall命名的,並經常用希臘字母τ(tau)表示其值。Kendall相關係數用於反映分類變數相關性的指標,適用於兩個分類變數均為有序分類的情況,Kendall相關係數的取值範圍在-1到1之間,當τ為1時,表示兩個隨機變數擁有一致的等級相關性;當τ為-1時,表示兩個隨機變數擁有完全相反的等級相關性;當τ為0時,表示兩個隨機變數是相互獨立的。
三、Spearman相關係數
Spearman等級相關係數又稱秩相關係,它以Charles Spearman命名,並經常用希臘字母ρ(rho)表示其值。它是利用兩變數的秩次大小作線性相關分析,Spearman等級相關係數用來估計兩個變數X、Y之間的相關性,其中變數間的相關性可以使用單調函式來描述。如果兩個變數取值的兩個集合中均不存在相同的兩個元素,那麼,當其中一個變數可以表示為另一個變數的很好的單調函式時(即兩個變數的變化趨勢相同),兩個變數之間的ρ可以達到+1或-1。
四、Matlab程式
1.X與Y是兩個變數取值所構成的向量
Pearson相關係數:corr(X,Y,'type','Pearson')
Kendall相關係數:corr(X,Y,'type','Kendall')
Spearman相關係數:corr(X,Y,'type','Spearman')
2.X是一個數據矩陣,列為個變數取值
Pearson相關係數:corr(X,'type','Pearson')
Kendall相關係數:corr(X,'type','Kendall')
Spearman相關係數:corr(X,'type','Spearman')
1.corrcoef
corrcoef(X):返回從矩陣X形成的一個相關係數矩陣,若X是一個m*n的矩陣,那麼得到的相關係數矩陣A就是一個n*n的對稱矩陣,A中的第i行第j列的元素表示的就是X第i列和第j列的相關係數。
corrcoef(X,Y):它的作用和corrcoef([X,Y])是一樣的,表示序列x和序列y的相關係數,得到的結果是一個2*2矩陣,其中對角線上的元素分別表示x和y的自相關,非對角線上的元素分別表示x與y的相關係數和y與x的相關係數,兩個是相等的。
corrcoef函式算出來的是皮爾遜相關係數。
corrcoef函式計算相關係數是在matlab提供的cov函式基礎上進行計算的,形成的矩陣是
2.corr
corr(X)輸出的結果和corrcoef是一致的,但是corr可以自己選擇相關係數的型別。matlab提供三種,預設的是皮爾遜相關係數,剩下的兩種是kendall和spearman.
相關程度與相關函式的之間的聯絡
在概率論和統計學中,相關(Correlation,或稱相關係數或關聯絡數),顯示兩個隨機變數之間線性關係的強度和方向。在統計學中,相關的意義是用來衡量兩個變數相對於其相互獨立的距離。最常用的是皮爾遜積矩相關係數。其定義是兩個變數協方差除以兩個變數的標準差(方差的平方根)。
相關係數只是一個比率,不是等單位量度,無什麼單位名稱,也不是相關的百分數,一般取小數點後兩位來表示。相關係數的正負號只表示相關的方向,絕對值表示相關的程度。因為不是等單位的度量,因而不能說相關係數0.7是0.35兩倍,只能說相關係數為0.7的二列變數相關程度比相關係數為0.35的二列變數相關程度更為密切和更高。也不能說相關係數從0.70到0.80與相關係數從0.30到0.40增加的程度一樣大。
對於相關係數的大小所表示的意義目前在統計學界尚不一致,但通常按下是這樣認為的:
相關係數 相關程度
0.00-±0.30 微相關
±0.30-±0.50 實相關
±0.50-±0.80 顯著相關
±0.80-±1.00 高度相關