在學習稀疏自編碼器之前，需要讀者有BP神經網路的基礎

1. 為什麼要用稀疏自編碼器

  對於沒有帶類別標籤的資料，由於為其增加類別標記是一個非常麻煩的過程，因此我們希望機器能夠自己學習到樣本中的一些重要特徵。通過對隱藏層施加一些限制，能夠使得它在惡劣的環境下學習到能最好表達樣本的特徵，並能有效地對樣本進行降維。這種限制可以是對隱藏層稀疏性的限制。
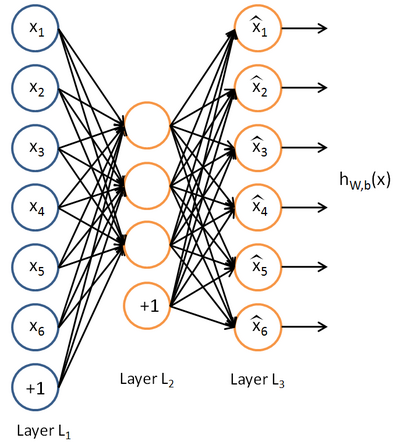
  如果給定一個神經網路，我們假設其輸出與輸入是相同的，然後訓練調整其引數，得到每一層中的權重。自然地，我們就得到了輸入的幾種不同表示（每一層代表一種表示），這些表示就是特徵。自動編碼器就是一種儘可能復現輸入訊號的神經網路。為了實現這種復現，自動編碼器就必須捕捉可以代表輸入資料的最重要的因素，就像PCA那樣，找到可以代表原資訊的主要成分。
  當然，我們還可以繼續加上一些約束條件得到新的Deep Learning方法，如：如果在AutoEncoder的基礎上加上L1的Regularity限制（L1主要是約束隱含層中的節點中大部分都要為0，只有少數不為0，這就是Sparse名字的來源），我們就可以得到Sparse AutoEncoder法。
  之所以要將隱含層稀疏化，是由於，如果隱藏神經元的數量較大（可能比輸入畫素的個數還要多），不稀疏化我們無法得到輸入的壓縮表示。具體來說，如果我們給隱藏神經元加入稀疏性限制，那麼自編碼神經網路即使在隱藏神經元數量較多的情況下仍然可以發現輸入資料中一些有趣的結構。

2. 稀疏自編碼器的解釋

稀疏性可以被簡單地解釋如下。如果當神經元的輸出接近於1的時候我們認為它被啟用，而輸出接近於0的時候認為它被抑制，那麼使得神經元大部分的時間都是被抑制的限制則被稱作稀疏性限制。這裡我們假設的神經元的啟用函式是sigmoid函式。如果你使用tanh作為啟用函式的話，當神經元輸出為-1的時候，我們認為神經元是被抑制的。

3. 模型

我們的目標是，使得hw,b(x)=x。並且通過隱含層，得到輸入的壓縮表示。

在神經網路裡面，我們得到的隱含層輸出用a表示。在這裡，我們將其轉換一下概念。a(2)j是隱含層第j個單元的輸出。a(2)j（x(i)）表示在給定輸入為 x 情況下，自編碼神經網路隱藏神經元 j 的啟用度。 進一步，讓
ρ

表示隱藏神經元 j 的平均活躍度（在訓練集上取平均）。我們可以近似的加入一條限制。

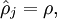
其中， ρ 是稀疏性引數，通常是一個接近於0的較小的值（比如 ρ= 0.05 ）。換句話說，我們想要讓隱藏神經元 ρˆ的平均活躍度接近0.05。為了滿足這一條件，隱藏神經元的活躍度必須接近於0。
為了實現這一限制，我們將會在我們的優化目標函式中加入一個額外的懲罰因子，而這一懲罰因子將懲罰那些ρˆ 和 ρ 有顯著不同的情況從而使得隱藏神經元的平均活躍度保持在較小範圍內。懲罰因子的具體形式有很多種合理的選擇，我們將會選擇以下這一種(KL散度)：

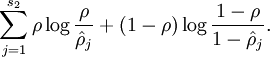
其中為了方便書寫：

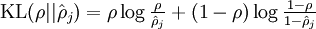
這樣，神經網路整體代價函式就可以表示為：

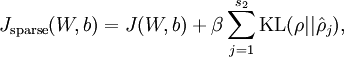
然後我們基於此再推導一次神經網路的反向傳播演算法。

最後我們得到，原本的神經網路誤差項：

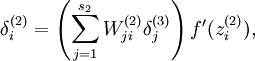
變成：

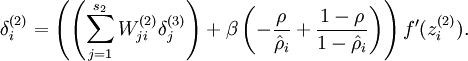
接下來就是訓練神經網路，直到收斂了。到最後，我們可以得到輸入層到隱含層的權重，利用這我們可以知道我們學習到了什麼。具體可參考視覺化自編碼器訓練結果

4.程式碼實現

由於是ufldl的教程，github上已經有開源的實現。
python實現
matla實現
讀者可以將原始碼下載回來，在自己的電腦上跑。但學習一個新演算法，最好的方式還是能夠自己能夠實現一次。所以以後有時間我會更新自己的稀疏自編碼器的實現。

參考文獻：