Time Limit: 5000MS Memory Limit: 65536K
Total Submissions: 5459 Accepted: 2262

Description
Some of you may have played a game called ‘Blocks’. There are n blocks in a row, each box has a color. Here is an example: Gold, Silver, Silver, Silver, Silver, Bronze, Bronze, Bronze, Gold.
The corresponding picture will be as shown below:

                        Figure 1

If some adjacent boxes are all of the same color, and both the box to its left(if it exists) and its right(if it exists) are of some other color, we call it a ‘box segment’. There are 4 box segments. That is: gold, silver, bronze, gold. There are 1, 4, 3, 1 box(es) in the segments respectively.

Every time, you can click a box, then the whole segment containing that box DISAPPEARS. If that segment is composed of k boxes, you will get k*k points. for example, if you click on a silver box, the silver segment disappears, you got 4*4=16 points.

Now let’s look at the picture below:

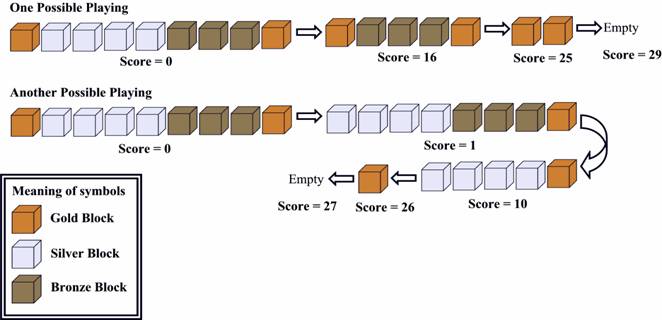
                       Figure 2
 

The first one is OPTIMAL.

Find the highest score you can get, given an initial state of this game.

Input
The first line contains the number of tests t(1<=t<=15). Each case contains two lines. The first line contains an integer n(1<=n<=200), the number of boxes. The second line contains n integers, representing the colors of each box. The integers are in the range 1~n.

Output
For each test case, print the case number and the highest possible score.

Sample Input

2
9
1 2 2 2 2 3 3 3 1
1
1

Sample Output

Case 1: 29
Case 2: 1
解題思路：

click_box(i,j,ex_len)
表示:
大塊j的右邊已經有一個長度為ex_len的大塊(該大塊可能是在合併過程中形成的，不妨就稱其為ex_len)， 且j的顏色和ex_len相同，在此情況下將 i 到j以及ex_len都消除所能得到的最高分。於是整個問題就是求： click_box(0,n-1,0)
求click_box(i,j,ex_len)時，有兩種處理方法，取最優者並且假設j和ex_len合併後的大塊稱作 Q
1) 將Q直接消除，這種做法能得到的最高分就是：
click_box(i,j-1,0) + (len[j]+ex_len)2
2) 期待Q以後能和左邊的某個同色大塊合併。需要列舉可能和Q合併的大塊。假設讓大塊k和Q合併，則此時能得到的最大分數是：
click_box(i,k,len[j]+ex_len) + click_box(k+1,j-1,0)
遞迴的終止條件是什麼？
i == j;

#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;

const int MAXN = 205;
struct Block{
    int len;
    int color;
}block[MAXN];
int dp[MAXN][MAXN][MAXN];

int dfs(int start, int end, int add)
{
    if (dp[start][end][add]) {
        return dp[start][end][add];
    }
    int ret = block[end].len + add;
    ret *= ret;
    if (end == start) {
        return dp[start][end][add] = ret;
    }
    ret += dfs(start, end - 1, 0);
    for (int i = end - 1; i >= start; i--) {
        if (block[i].color == block[end].color) {
            int retS = dfs(start, i, block[end].len + add) + dfs(i + 1, end - 1, 0);
            if (retS > ret) {
                ret = retS;
                break;
                //return dp[start][end][add] = retS;
            }
        }
    }
    return dp[start][end][add] = ret;
}

int main()
{
    int t, n;
    scanf("%d", &t);
    for (int i = 1; i <= t; i++){
        memset(dp, 0, sizeof(dp));
        scanf("%d", &n);
        int color, end = 0;
        scanf("%d", &color);
        block[end].color = color;
        block[end].len = 1;
        n--;
        while (n--) {
            scanf("%d", &color);
            if (color == block[end].color) {
                block[end].len++;
            }
            else {
                end++;
                block[end].color = color;
                block[end].len = 1;
            }
        }
        int score = dfs(0, end, 0);
        printf("Case %d: %d\n", i, score);
    }
    return 0;
}