如果搜尋文件有很多重複的文字，比如一些文件是轉載的其他的文件，只是佈局不同，那麼就需要把重複的文件去掉，一方面節省儲存空間，一方面節省搜尋時間，當然搜尋質量也會提高。
simhash是google用來處理海量文字去重的演算法。

1. 原理：

simhash將一個文件轉換成一個64位的位元組，暫且稱之為簽名值，然後判斷兩篇文件的簽名值的距離是不是小於等於n（根據經驗這個n一般取值為3），就可以判斷兩個文件是否相似。

2. simhash和傳統的hash演算法有什麼不同？

simhash和傳統的hash都可以將文件轉換為一個簽名值，它們有什麼不同呢？
simhash基於區域性敏感雜湊框架，即如果兩個文件內容越相似，則其對應的兩個雜湊值也越接近，所以就可以將文字內容相似性問題轉換為雜湊值的相近性問題。
而傳統的hash演算法只負責將原始內容儘量均勻隨機地對映為一個簽名值，原理上相當於偽隨機數產生演算法。產生的兩個簽名，如果相等，說明原始內容在一定概率下是相等的；如果不相等，除了說明原始內容不相等外，不再提供任何資訊，因為即使原始內容只相差一個位元組，所產生的簽名也很可能差別極大。而simhash的簽名值除了提供原始內容是否相等的資訊外，還能額外提供不相等的原始內容的差異程度的資訊。

3. simhash演算法步驟描述：

simhash演算法步驟見下圖：

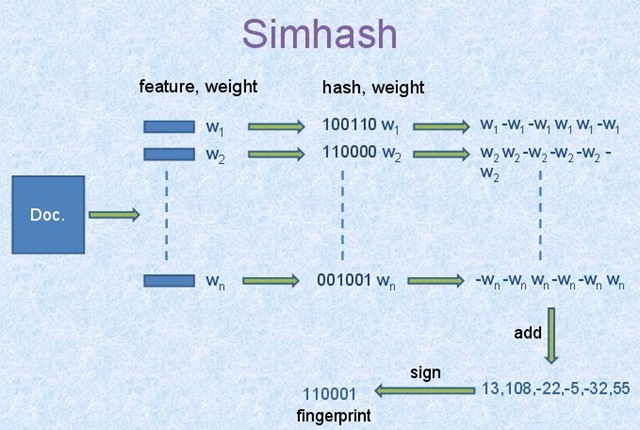
1）首先從文件內容中抽取n個能表徵文件的特徵，至於具體實現，則可以採用不同的抽取方法，經過此步驟，獲得文件的特徵詞及其權值對，即圖中的n個(feature,weight)。方法之一可以參考 使用向量空間模型（df-idf）計算搜尋文件與查詢詞的相關性中的（6）使用TF*IDF框架提取文件和使用者查詢的特徵詞及其權重。
2）利用一個雜湊函式將每個特徵詞對映成bit_count位的二進位制數值。圖中所示演算法將每個特徵詞轉換為了bit_count=6的二進位制數值，這樣每個（feature，weight）就轉換為圖中的（hash，weight）了。
3）利用權重改寫特徵的二進位制hash值，將權重融入其中，將bit_count位的二進位制數值改寫為bit_count個實數，形成一個實數向量。假設某個特徵的權值是w，則對二進位制向量做如下改寫：如果二進位制的某個位元位是數值1，則實數向量中對應位置改寫為數值w；如果位元位數值為0，則實數向量中對應位置改寫為數值-w，即權值的負數。通過以上規則，就將bit_count的二進位制數改為了特徵權重的實數向量。
4）當n個特徵都進行了上述改寫後，對所有特徵的實數向量累加獲得一個代表文件整體的實數向量。累加規則也很簡單，就是將對應位置的數值累加即可。
5）再次將實數向量轉換為bit_count位的二進位制數值。轉換規則如下：如果對應位置的數值大於0，則設定為二進位制數字1；如果小於等於0，則設定為二進位制數字0。如此就得到了文件的資訊指紋，即最終的simhash值。
上圖將文件特徵詞hash為6位的二進位制數值，在實際計算中，往往會將長度設定為64，即每個文件轉換為64位元的simhash值。

4. 利用simhash對文件去重

將文件轉換為simhash值後，如何利用simhash值比較兩個文件的相似性呢？對於兩個文件A和B，其內容相似性可以通過比較simhash值的差異來體現，內容越相似，則二進位制數值對應位置的相同的0或者1越多，兩個二進位制數值不同的二進位制位數稱為“海明距離”（也就是兩個二進位制數值xor 後二進位制中1的個數）。
舉例如下：

A = 100111;
B = 101010;
hamming_distance(A, B) = count_1(A xor B) = count_1(001101) = 3;

當我們算出所有文件的simhash值之後，需要計算文件 A和文件 B之間是否相似的條件是：A和B的海明距離是否小於等於n

5. simhash的c++實現：

6. 處理海量文件

1）利用hash查詢海量simhash（一）
海量的網頁經過上述步驟，轉換為海量的二進位制數值，此時如果新抓取到一個網頁，如何找出近似重複的內容呢？
一個很容易想到的方式是一一匹配，將新網頁轉換為64位元的二進位制數值，之後和所有網頁的simhash一一比較，如果兩者的海明距離小於等於3，則可以認為是近似重複網頁。這種方法雖然直觀，但是計算量過大，所以在以億計的網頁中，實際是不太可行的。
假設我們要尋找海明距離3以內的數值，根據抽屜原理，只要我們將整個64位的二進位制串劃分為4塊，無論如何，匹配的兩個simhash之間至少有一塊區域是完全相同的，所以我們可以借鑑hash查詢的方法，把這一區域的數值作為key，先找到哪些simhash的key等於目標simhash的key，然後在這些simhash集合中查詢那些海明距離在3以內的數值。
這就要求我們在儲存simhash時，需要把key相同的simhash儲存在一起。
但又因為我們無法事先得知完全相同的是哪一塊區域，所以四個區域的每個區域都應該作為我們查詢value的key值。
具體做法如下：

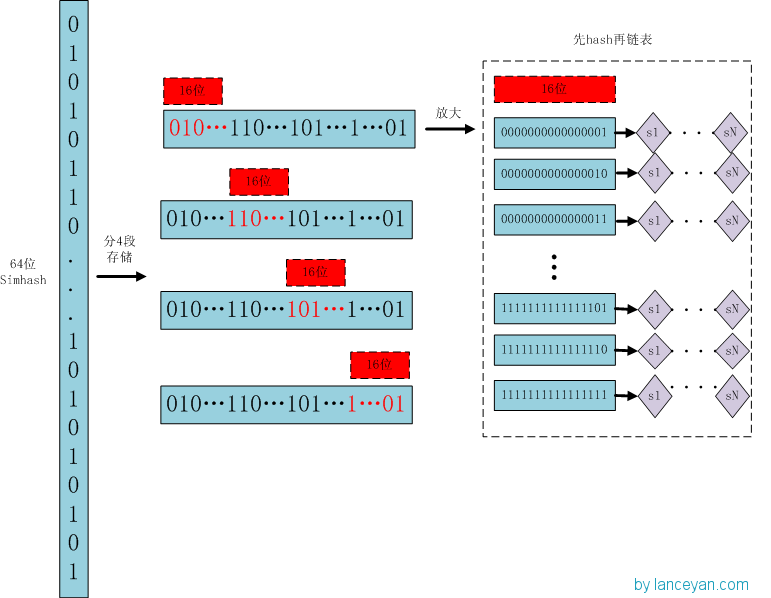
儲存：
1）將64位的simhash code平均分成4個區域，每個區域都有16bit。（圖上紅色的16位）
2）分別以4個16位二進位制碼作為key，查詢該key對應位置上是否有元素。（放大後的16位）
3）對應位置沒有元素，直接追加到連結串列上；對應位置有則直接追加到連結串列尾端。（圖上的 S1 — SN）
查詢：
1）將需要比較的simhash code拆分成4個16位的二進位制碼。
2）分別以4個16位二進位制碼作為key，查詢simhash集合每個key對應位置上是否有元素。
3）如果有元素，則把連結串列拿出來順序查詢比較，查詢那些海明距離小於3的數值，整個過程完成。
2）空間和時間開銷（一）
這種方法，由於每個hashcode最多有4個key（顯然如果有兩個區域的code值相同，則key小於4個），每個key都要儲存一遍，所以需要的空間是原來的4倍。但每個key對應的simhash平均數量變為simhash數量總和的1/216，所以搜尋時間是一一搜索的4216。
3）利用hash查詢海量simhash（二）
假設我們還是要尋找海明距離3以內的數值，如果我們要把4個區域變成5個區域，所花的空間和時間又變成多少呢？
因為根據抽屜原理，如果分成5個區域，則至少有兩個區域是完全相同的，所以需要將這兩塊區域的值作為key，查詢時先找到哪些simhash的key等於目標simhash的key，然後在這些simhash集合中查詢那些海明距離在3以內的數值。
究竟是哪兩塊區域相同共有C25=10種情況，所以兩個區域組成的這10個key都應該作為我們查詢value的key值。
具體做法如下：
儲存：
1）將64位的simhash code分成5個區域，每個區域分別有13 13 13 13 12位。
2）分別以10種26位（13+13）或25位（13+12）二進位制碼作為key，查詢該key對應位置上是否有元素
3）對應位置沒有元素，直接追加到連結串列上；對應位置有則直接追加到連結串列尾端
查詢：
1）將需要比較的simhash code分成5個區域，每個區域分別有13 13 13 13 12位。
2）分別以10種26位（13+13）或25位（13+12）二進位制碼作為key，查詢simhash集合對應key位置上是否有元素。
3）如果有元素，則把連結串列拿出來順序查詢比較，查詢那些海明距離小於3的數值，整個過程完成。
4）空間和時間開銷（二）
這種方法，由於每個hashcode最多有10個key，每個key都要儲存一遍，所以需要的空間是原來的10倍。但每個key對應的simhash平均數量為simhash數量總和的1226或1225，所以搜尋時間是一一搜索的10226或10225。

7. 儲存simhash的資料結構：

根據6，儲存simhash需要用的資料結構應該為：hash < int,vector < uint_64>>吧。

8. 參考：