【專案 - 用二叉樹求解代數表示式】
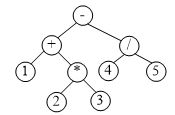
　　用二叉樹來表示代數表示式，樹的每一個分支節點代表一個運算子，每一個葉子節點代表一個運算數（為簡化，只支援二目運算的+、-、*、/，不加括號，運算數也只是一位的數字字元。本專案只考慮輸入合乎以上規則的情況）。請設計演算法，（1）根據形如“1+2∗3−4/5 ”的字串代表的表示式，構造出對應的二叉樹（如圖），用後序遍歷的思路計算表示式的值時，能體現出先乘除後加減的規則；（2）對構造出的二叉樹，計算出表示式的值。

[參考解答] 程式中的btree.h，見二叉樹演算法庫。

#include <stdio.h>
#include <string.h>
 

#include <malloc.h>
#include "btree.h"

//用s[i]到s[j]之間的字串，構造二叉樹的表示形式
BTNode *CRTree(char s[],int i,int j)
{
    BTNode *p;
    int k,plus=0,posi;
    if (i==j)    //i和j相同，意味著只有一個字元，構造的是一個葉子節點
    {
        p=(BTNode *)malloc(sizeof(BTNode));   //分配儲存空間
        p->data=s[i];                         //值為s[i]
 

        p->lchild=NULL;
        p->rchild=NULL;
        return p;
    }
    //以下為i!=j的情況
    for (k=i; k<=j; k++)
        if (s[k]=='+' || s[k]=='-')
        {
            plus++;
            posi=k;              //最後一個+或-的位置
        }
    if (plus==0)                 //沒有+或-的情況(因為若有+、-，前面必會執行plus++)
 

        for (k=i; k<=j; k++)
            if (s[k]=='*' || s[k]=='/')
            {
                plus++;
                posi=k;
            }
    //以上的處理考慮了優先將+、-放到二叉樹較高的層次上
    //由於將來計算時，運用的是後序遍歷的思路
    //處於較低層的乘除會優先運算
    //從而體現了“先乘除後加減”的運演算法則
    //建立一個分支節點，用檢測到的運算子作為節點值
    if (plus!=0)
    {
        p=(BTNode *)malloc(sizeof(BTNode));
        p->data=s[posi];                //節點值是s[posi]
        p->lchild=CRTree(s,i,posi-1);   //左子樹由s[i]至s[posi-1]構成
        p->rchild=CRTree(s,posi+1,j);   //右子樹由s[poso+1]到s[j]構成
        return p;
    }
    else       //若沒有任何運算子，返回NULL
        return NULL;
}

double Comp(BTNode *b)
{
    double v1,v2;
    if (b==NULL)
        return 0;
    if (b->lchild==NULL && b->rchild==NULL)  //葉子節點，應該是一個數字字元（本專案未考慮非法表示式）
        return b->data-'0';    //葉子節點直接返回節點值，結點中儲存的數字用的是字元形式，所以要-'0'
    v1=Comp(b->lchild); //先計算左子樹
    v2=Comp(b->rchild); //再計算右子樹
    switch(b->data)     //將左、右子樹運算的結果再進行運算，運用的是後序遍歷的思路
    {
    case '+':
        return v1+v2;
    case '-':
        return v1-v2;
    case '*':
        return v1*v2;
    case '/':
        if (v2!=0)
            return v1/v2;
        else
            abort();
    }
}

int main()
{
    BTNode *b;
    char s[MaxSize]="1+2*3-4/5";
    printf("代數表示式%s\n",s);
    b=CRTree(s,0,strlen(s)-1);
    printf("對應二叉樹:");
    DispBTNode(b);
    printf("\n表示式的值:%g\n",Comp(b));
    DestroyBTNode(b);
    return 0;
}