Pocket Cube

Time Limit: 20000/10000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 757 Accepted Submission(s): 234


Problem Description Pocket Cube is a 3-D combination puzzle. It is a 2 × 2 × 2 cube, which means it is constructed by 8 mini-cubes. For a combination of 2 × 2 mini-cubes which sharing a whole cube face, you can twist it 90 degrees in clockwise or counterclockwise direction, this twist operation is called one twist step.
Considering all faces of mini-cubes, there will be totally 24 faces painted in 6 different colors (Indexed from 0), and there will be exactly 4 faces painted in each kind of color. If 4 mini-cubes' faces of same color rely on same large cube face, we can call the large cube face as a completed face.

Now giving you an color arrangement of all 24 faces from a scrambled Pocket Cube, please tell us the maximum possible number of completed faces in no more than N twist steps.
Index of each face is shown as below:



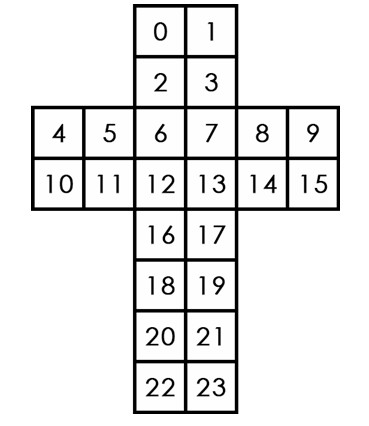
Input There will be several test cases. In each test case, there will be 2 lines. One integer N (1 ≤ N ≤ 7) in the first line, then 24 integers Ci separated by a single space in the second line. For index 0 ≤ i < 24, Ci is color of the corresponding face. We guarantee that the color arrangement is a valid state which can be achieved by doing a finite number of twist steps from an initial cube whose all 6 large cube faces are completed faces.
Output For each test case, please output the maximum number of completed faces during no more than N twist step(s).
Sample Input 1 0 0 0 0 1 1 2 2 3 3 1 1 2 2 3 3 4 4 4 4 5 5 5 5 1 0 4 0 4 1 1 2 5 3 3 1 1 2 5 3 3 4 0 4 0 5 2 5 2
Sample Output 6 2
Source 每次旋轉有六種情況，最多旋轉7次，6^7的時間複雜度，用佇列來寫，比較所有的情況，找出最大值，但是不知為毛，用c++提交，不是超時，就是超記憶體，用 G++提交然後就對了，鬱悶。。。

#include<stdio.h>
#include<queue>
using namespace std;
struct node
{
    int a[26];
    int step;
}b,s;
int n;
int judge(struct node s)
{
    int ans=0;
    if(s.a[0]==s.a[1]&&s.a[0]==s.a[2]&&s.a[0]==s.a[3])
        ans++;
    if(s.a[4]==s.a[5]&&s.a[4]==s.a[10]&&s.a[4]==s.a[11])
        ans++;
    if(s.a[6]==s.a[7]&&s.a[6]==s.a[12]&&s.a[6]==s.a[13])
        ans++;
    if(s.a[8]==s.a[9]&&s.a[8]==s.a[14]&&s.a[8]==s.a[15])
        ans++;
    if(s.a[16]==s.a[17]&&s.a[16]==s.a[18]&&s.a[16]==s.a[19])
        ans++;
    if(s.a[20]==s.a[21]&&s.a[20]==s.a[22]&&s.a[20]==s.a[23])
        ans++;
    return ans;
}
void bfs(struct node s)
{
    int max,ans,c,d;
    queue<node>q;
    s.step=0;
    q.push(s);
    max=-1;
    while(!q.empty())
    {
        s=q.front();
        q.pop();
        ans=judge(s);
        if(ans>max)
        {
            max=ans;
            if(ans==6)
                break;
        }
        if(s.step<n)
        {
            b=s;
            b.a[0]=s.a[6];   b.a[2]=s.a[12];  b.a[6]=s.a[16];
            b.a[12]=s.a[18]; b.a[16]=s.a[20]; b.a[18]=s.a[22];
            b.a[20]=s.a[0];  b.a[22]=s.a[2];
            b.a[4]=s.a[5];   b.a[5]=s.a[11];
            b.a[11]=s.a[10]; b.a[10]=s.a[4];
            b.step=s.step+1;  q.push(b);

            b=s;
            b.a[22]=s.a[18]; b.a[20]=s.a[16]; b.a[18]=s.a[12];
            b.a[16]=s.a[6];  b.a[12]=s.a[2];  b.a[6]=s.a[0];
            b.a[2]=s.a[22];  b.a[0]=s.a[20];
            b.a[4]=s.a[10];  b.a[10]=s.a[11];
            b.a[11]=s.a[5];  b.a[5]=s.a[4];
            b.step=s.step+1; q.push(b);

            b=s;
            b.a[4]=s.a[18]; b.a[10]=s.a[19]; b.a[18]=s.a[15];
            b.a[19]=s.a[9]; b.a[15]=s.a[1];  b.a[9]=s.a[0];
            b.a[1]=s.a[4];  b.a[0]=s.a[10];
            b.a[22]=s.a[20]; b.a[20]=s.a[21];
            b.a[21]=s.a[23]; b.a[23]=s.a[22];
            b.step=s.step+1; q.push(b);

            b=s;
            b.a[4]=s.a[1];   b.a[10]=s.a[0]; b.a[0]=s.a[9];
            b.a[1]=s.a[15];  b.a[9]=s.a[19]; b.a[15]=s.a[18];
            b.a[19]=s.a[10]; b.a[18]=s.a[4];
            b.a[22]=s.a[23]; b.a[23]=s.a[21];
            b.a[21]=s.a[20]; b.a[20]=s.a[22];
            b.step=s.step+1; q.push(b);

            b=s;
            b.a[14]=s.a[21]; b.a[15]=s.a[20]; b.a[21]=s.a[10];
            b.a[20]=s.a[11]; b.a[10]=s.a[12]; b.a[11]=s.a[13];
            b.a[12]=s.a[14]; b.a[13]=s.a[15];
            b.a[18]=s.a[16]; b.a[16]=s.a[17];
            b.a[17]=s.a[19]; b.a[19]=s.a[18];
            b.step=s.step+1; q.push(b);

            b=s;
            b.a[13]=s.a[11]; b.a[12]=s.a[10]; b.a[11]=s.a[20];
            b.a[10]=s.a[21]; b.a[20]=s.a[15]; b.a[21]=s.a[14];
            b.a[15]=s.a[13]; b.a[14]=s.a[12];
            b.a[18]=s.a[19]; b.a[19]=s.a[17];
            b.a[17]=s.a[16]; b.a[16]=s.a[18];
            b.step=s.step+1; q.push(b);
        }
    }
    printf("%d\n",max);
}
int main()
{
    int i;
    while(scanf("%d",&n)!=EOF)
    {
        for(i=0;i<=23;i++)
            scanf("%d",&s.a[i]);
       bfs(s);
    }
    return 0;
}