函式定義

tf.nn.conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None, data_format=None, name=None)

功能：在給定4-D 輸入和fliters的情況下，計算二維卷積。

input的shape: [batch, in_height, in_width, in_channels]
filter的shape: [filter_height, filter_width, in_channels, out_channels]

計算過程如下：
（１）展平filter成如下2-D matrix，其shape: [filter_height * filter_width * in_channels, output_channels]
（２）從input tensor中提取patches構成一個virtual tensor, 其shape: [batch, out_height, out_width, filter_height * filter_width * in_channels]
（３）對於每一個patch,　右乘上（１）中的filter matrix。即[batch, out_height, out_width, filter_height * filter_width * in_channels]　x [filter_height * filter_width * in_channels, output_channels]，其結果的shape就是[batch, out_height, out_width, output_channels]。

【注：必須有 strides[0] = strides[3] = 1】。絕大多數情況下，水平的stride和豎直的stride一樣，即strides = [1, stride, stride, 1]。

輸出結果的shape計算：
‘SAME’ 型別的padding,其輸出的height和width計算如下：
out_height = ceil(float(in_height) / float(strides[1])) ceil：向上取整
out_width = ceil(float(in_width) / float(strides[2]))

‘VALID’型別的padding, 其輸出的height和width計算如下：
out_height = ceil(float(in_height – filter_height + 1) / float(strides[1]))
out_width = ceil(float(in_width – filter_width + 1) / float(strides[2]))

【注：tensorflow中的卷積，嚴格上來說是cross-correlation，而不是卷積。因為在計算的過程中，沒有對filter進行翻轉，而嚴格的卷積計算是需要對filter進行翻轉的！！！】

程式碼驗證

tensorflow中的tf.nn.conv2d函式，實際上相當於用filter，以一定的步長stride在image上進行滑動，計算重疊部分的內積和，即為卷積結果。下面從定義出發對tf.nn.conv2d函式的功能進行驗證：

# -*- coding: utf-8 -*-

from __future__ import division
import tensorflow as
 
 tf
import numpy as np
import math
import pandas as pd

input_arr = np.zeros((12, 15), dtype=np.float32)
number = 0
for row_idx in range(input_arr.shape[0]):
    for col_idx in range(input_arr.shape[1]):
        input_arr[row_idx][col_idx] = number
        number += 1

number = 6
w_arr = np.zeros((2, 3), dtype=np.float32)
for row_idx in range(w_arr.shape[0]):
    for col_idx in range(w_arr.shape[1]):
        w_arr[row_idx][col_idx] = number
        number -= 1

stride = [1, 1, 1, 1]

# 從卷積的定義【實際上不是卷積，而是cross-correlation】進行計算驗證---對VALID型別卷積進行驗證
res_shape_0 = int(math.ceil((input_arr.shape[0] - w_arr.shape[0] + 1) / stride[1]))
res_shape_1 = int(math.ceil((input_arr.shape[1] - w_arr.shape[1] + 1) / stride[2]))
validation_res = np.zeros(shape=(res_shape_0, res_shape_1), dtype=np.float32)

for row_idx in range(validation_res.shape[0]):
    for col_idx in range(validation_res.shape[1]):
        patch = input_arr[row_idx:row_idx+w_arr.shape[0], col_idx:col_idx+w_arr.shape[1]]
        # 這裡的　*　實際上代表的是點積，即對應元素位置相乘
        res = np.sum(patch * w_arr)
        validation_res[row_idx][col_idx] = res

print('result of convolution from its definition: validation_res')
print validation_res
pd.DataFrame(validation_res).to_csv('Results/validation_res.csv', index=False, header=False)

input_arr = np.reshape(input_arr, [1, input_arr.shape[0], input_arr.shape[1], 1])
w_arr = np.reshape(w_arr, [w_arr.shape[0], w_arr.shape[1], 1, 1])

# 相當於要輸入的圖片，shape: [1, 12, 15, 1]
net_in = tf.constant(value=input_arr, dtype=tf.float32)

# 相當於filter, shape: [2, 3, 1, 1]
W = tf.constant(value=w_arr, dtype=tf.float32)

# tensorflow卷積的計算結果：
# valid卷積結果, shape: [1, 11, 13, 1]
result_conv_valid = tf.nn.conv2d(net_in, W, stride, 'VALID', True)

# same卷積結果, shape: [1, 12, 15, 1]
result_conv_same = tf.nn.conv2d(net_in, W, stride, 'SAME', True)

sess = tf.Session()
sess.run(tf.global_variables_initializer())

valid_conv_res = sess.run(result_conv_valid)
same_conv_res = sess.run(result_conv_same)
sess.close()

print valid_conv_res.shape
valid_conv_res = np.reshape(valid_conv_res, [valid_conv_res.shape[1], valid_conv_res.shape[2]])
same_conv_res = np.reshape(same_conv_res, [same_conv_res.shape[1], same_conv_res.shape[2]])
print('tensorflow conv res: valid_conv_res')
print valid_conv_res
pd.DataFrame(valid_conv_res).to_csv('Results/conv_res.csv', index=False, header=False)
pd.DataFrame(same_conv_res).to_csv('Results/result_conv_same.csv', index=False, header=False)

上面程式碼，只針對valid卷積型別進行了驗證，對same的卷積型別沒有驗證【same型別的卷積，其padding方式還不懂，求懂的高手指教】。計算結果儲存到了相應的csv檔案中。
（１）Tensorflow valid型別卷積計算結果：

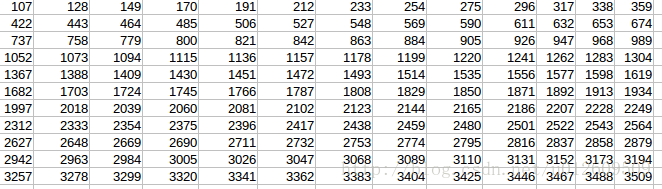
（２）Tensorflow same型別卷積計算結果：

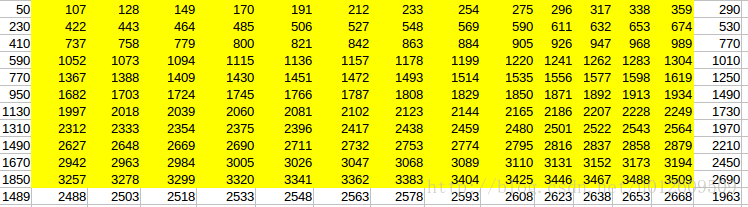
（３）從卷積定義出發，valid型別卷積計算結果：

可以看出，其驗證結果是正確的。並且same和valid的卷積結果，除邊緣部分外，其餘的值都是一樣的。