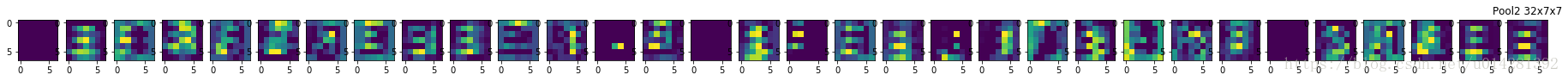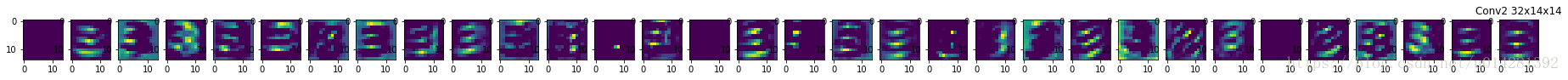卷積神經網路CNN:Tensorflow實現(以及對卷積特徵的視覺化)

阿新 • • 發佈：2019-01-24

本文主要是實現了一個簡單的卷積神經網路,並對卷積過程中的提取特徵進行了視覺化.
這裡寫圖片描述

　　卷積神經網路最早是為了解決影象識別的問題,現在也用在時間序列資料和文字資料處理當中,卷積神經網路對於資料特徵的提取不用額外進行,在對網路的訓練的過程當中,網路會自動提取主要的特徵.
　　卷積神經網路直接用原始影象的全部畫素作為輸入,但是內部為非全連線結構.因為影象資料在空間上是有組織結構的,每一個畫素在空間上和周圍的畫素是有關係的,和相距很遠的畫素基本上是沒什麼聯絡的,每個神經元只需要接受區域性的畫素作為輸入,再將區域性資訊彙總就能得到全域性資訊.
　　權值共享和池化兩個操作使網路模型的引數大幅的減少,提高了模型的訓練效率.

權值共享:
　　在卷積層中可以有多個卷積核,每個卷積核與原始影象進行卷積運算後會映射出一個新的2D影象,新影象的每個畫素都來自同一個卷積核.這就是權值共享.
- 池化:
  降取樣,對卷積(濾波)後,經過啟用函式處理後的影象,保留畫素塊中灰度值最高的畫素點(保留最主要的特徵),比如進行 2X2的最大池化,把一個2x2的畫素塊降為1x1的畫素塊.

# 卷積網路的訓練資料為MNIST(28*28灰度單色影象)
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import 
 input_data

訓練引數

train_epochs = 100    # 訓練輪數
batch_size   = 100     # 隨機出去資料大小
display_step = 1       # 顯示訓練結果的間隔
learning_rate= 0.0001  # 學習效率
drop_prob    = 0.5     # 正則化,丟棄比例
fch_nodes    = 512     # 全連線隱藏層神經元的個數

網路結構

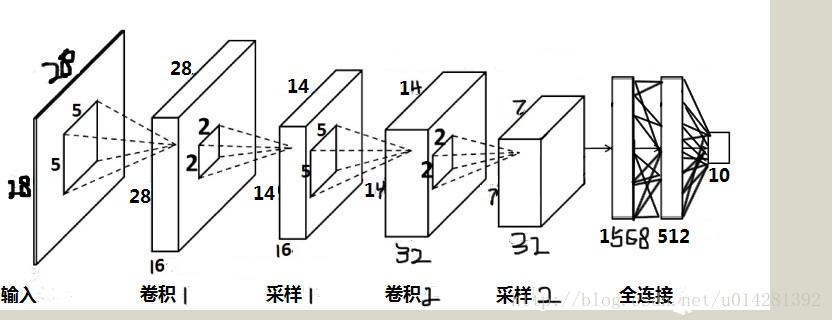
這裡寫圖片描述

輸入層為輸入的灰度影象尺寸:  -1 x 28 x 28 x 1 
第一個卷積層,卷積核的大小,深度和數量 (5, 5, 1, 16)
池化後的特徵張量尺寸:       -1 
 x 14 x 14 x 16
第二個卷積層,卷積核的大小,深度和數量 (5, 5, 16, 32)
池化後的特徵張量尺寸:       -1 x 7 x 7 x 32
全連線層權重矩陣         1568 x 512
輸出層與全連線隱藏層之間,  512 x 10

一些輔助函式

# 網路模型需要的一些輔助函式
# 權重初始化(卷積核初始化)
# tf.truncated_normal()不同於tf.random_normal(),返回的值中不會偏離均值兩倍的標準差
# 引數shpae為一個列表物件,例如[5, 5, 1, 32]對應
# 5,5 表示卷積核的大小, 1代表通道channel,對彩色圖片做卷積是3,單色灰度為1
# 最後一個數字32,卷積核的個數,(也就是卷基層提取的特徵數量)
#   顯式宣告資料型別,切記
def weight_init(shape):
    weights = tf.truncated_normal(shape, stddev=0.1,dtype=tf.float32)
    return tf.Variable(weights)

# 偏置的初始化
def biases_init(shape):
    biases = tf.random_normal(shape,dtype=tf.float32)
    return tf.Variable(biases)

# 隨機選取mini_batch
def get_random_batchdata(n_samples, batchsize):
    start_index = np.random.randint(0, n_samples - batchsize)
    return (start_index, start_index + batchsize)

# 全連線層權重初始化函式xavier
def xavier_init(layer1, layer2, constant = 1):
    Min = -constant * np.sqrt(6.0 / (layer1 + layer2))
    Max = constant * np.sqrt(6.0 / (layer1 + layer2))
    return tf.Variable(tf.random_uniform((layer1, layer2), minval = Min, maxval = Max, dtype = tf.float32))

# 卷積
def conv2d(x, w):
    return tf.nn.conv2d(x, w, strides=[1, 1, 1, 1], padding='SAME')

# 原始碼的位置在tensorflow/python/ops下nn_impl.py和nn_ops.py
# 這個函式接收兩個引數,x 是影象的畫素, w 是卷積核
# x 張量的維度[batch, height, width, channels]
# w 卷積核的維度[height, width, channels, channels_multiplier]
# tf.nn.conv2d()是一個二維卷積函式,
# stirdes 是卷積核移動的步長,4個1表示,在x張量維度的四個引數上移動步長
# padding 引數'SAME',表示對原始輸入畫素進行填充,卷積後對映的2D影象與原圖大小相等
# 填充,是指在原影象素值矩陣周圍填充0畫素點
# 如果不進行填充,假設 原圖為 32x32 的影象,卷積和大小為 5x5 ,卷積後對映影象大小 為 28x28

Padding

卷積核在提取特徵時的動作成為padding，它有兩種方式：SAME和VALID。卷積核的移動步長不一定能夠整除圖片畫素的寬度，所以在有些圖片的邊框位置有些畫素不能被卷積。這種不越過邊緣的取樣就叫做 valid padding，卷積後的影象面積小於原影象。為了讓卷積核覆蓋到所有的畫素，可以對邊緣位置進行0畫素填充，然後在進行卷積。這種越過邊緣的取樣是 same padding。如過移動步長為1，那麼得到和原圖一樣大小的影象。
    如果步長很大，超過了卷積核長度，那麼same padding，得到的特徵圖也會小於原來的影象。

# 池化
def max_pool_2x2(x):
    return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')

# 池化跟卷積的情況有點類似
# x 是卷積後,有經過非線性啟用後的影象,
# ksize 是池化滑動張量
# ksize 的維度[batch, height, width, channels],跟 x 張量相同
# strides [1, 2, 2, 1],與上面對應維度的移動步長
# padding與卷積函式相同,padding='VALID',對原影象不進行0填充

# x 是手寫影象的畫素值,y 是影象對應的標籤
x = tf.placeholder(tf.float32, [None, 784])
y = tf.placeholder(tf.float32, [None, 10])
# 把灰度影象一維向量,轉換為28x28二維結構
x_image = tf.reshape(x, [-1, 28, 28, 1])
# -1表示任意數量的樣本數,大小為28x28深度為一的張量
# 可以忽略(其實是用深度為28的,28x1的張量,來表示28x28深度為1的張量)

第一層卷積+池化


w_conv1 = weight_init([5, 5, 1, 16])                             # 5x5,深度為1,16個
b_conv1 = biases_init([16])
h_conv1 = tf.nn.relu(conv2d(x_image, w_conv1) + b_conv1)    # 輸出張量的尺寸:28x28x16
h_pool1 = max_pool_2x2(h_conv1)                                   # 池化後張量尺寸:14x14x16
# h_pool1 , 14x14的16個特徵圖

第二層卷積+池化


w_conv2 = weight_init([5, 5, 16, 32])                             # 5x5,深度為16,32個
b_conv2 = biases_init([32])
h_conv2 = tf.nn.relu(conv2d(h_pool1, w_conv2) + b_conv2)    # 輸出張量的尺寸:14x14x32
h_pool2 = max_pool_2x2(h_conv2)                                   # 池化後張量尺寸:7x7x32
# h_pool2 , 7x7的32個特徵圖

全連線層

# h_pool2是一個7x7x32的tensor,將其轉換為一個一維的向量
h_fpool2 = tf.reshape(h_pool2, [-1, 7*7*32])
# 全連線層,隱藏層節點為512個
# 權重初始化
w_fc1 = xavier_init(7*7*32, fch_nodes)
b_fc1 = biases_init([fch_nodes])
h_fc1 = tf.nn.relu(tf.matmul(h_fpool2, w_fc1) + b_fc1)

# 全連線隱藏層/輸出層
# 為了防止網路出現過擬合的情況,對全連線隱藏層進行 Dropout(正則化)處理,在訓練過程中隨機的丟棄部分
# 節點的資料來防止過擬合.Dropout同把節點資料設定為0來丟棄一些特徵值,僅在訓練過程中,
# 預測的時候,仍使用全資料特徵
# 傳入丟棄節點資料的比例
#keep_prob = tf.placeholder(tf.float32)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob=drop_prob)

# 隱藏層與輸出層權重初始化
w_fc2 = xavier_init(fch_nodes, 10)
b_fc2 = biases_init([10])

# 未啟用的輸出
y_ = tf.add(tf.matmul(h_fc1_drop, w_fc2), b_fc2)
# 啟用後的輸出
y_out = tf.nn.softmax(y_)

# 交叉熵代價函式
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y * tf.log(y_out), reduction_indices = [1]))

# tensorflow自帶一個計算交叉熵的方法
# 輸入沒有進行非線性啟用的輸出值 和 對應真實標籤
#cross_loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(y_, y))

# 優化器選擇Adam(有多個選擇)
optimizer = tf.train.AdamOptimizer(learning_rate).minimize(cross_entropy)

# 準確率
# 每個樣本的預測結果是一個(1,10)的vector
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_out, 1))
# tf.cast把bool值轉換為浮點數
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

# 全域性變數進行初始化的Operation
init = tf.global_variables_initializer()

# 載入資料集MNIST
mnist = input_data.read_data_sets('MNIST/mnist', one_hot=True)
n_samples = int(mnist.train.num_examples)
total_batches = int(n_samples / batch_size)

# 會話
with tf.Session() as sess:
    sess.run(init)
    Cost = []
    Accuracy = []
    for i in range(train_epochs):

        for j in range(100):
            start_index, end_index = get_random_batchdata(n_samples, batch_size)

            batch_x = mnist.train.images[start_index: end_index]
            batch_y = mnist.train.labels[start_index: end_index]
            _, cost, accu = sess.run([ optimizer, cross_entropy,accuracy], feed_dict={x:batch_x, y:batch_y})
            Cost.append(cost)
            Accuracy.append(accu)
        if i % display_step ==0:
            print ('Epoch : %d ,  Cost : %.7f'%(i+1, cost))
    print 'training finished'
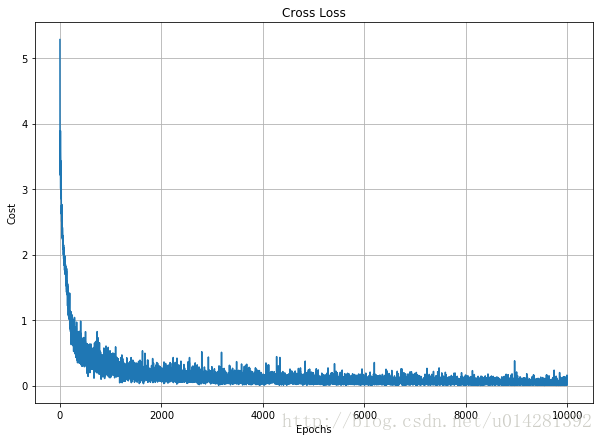
    # 代價函式曲線
    fig1,ax1 = plt.subplots(figsize=(10,7))
    plt.plot(Cost)
    ax1.set_xlabel('Epochs')
    ax1.set_ylabel('Cost')
    plt.title('Cross Loss')
    plt.grid()
    plt.show()
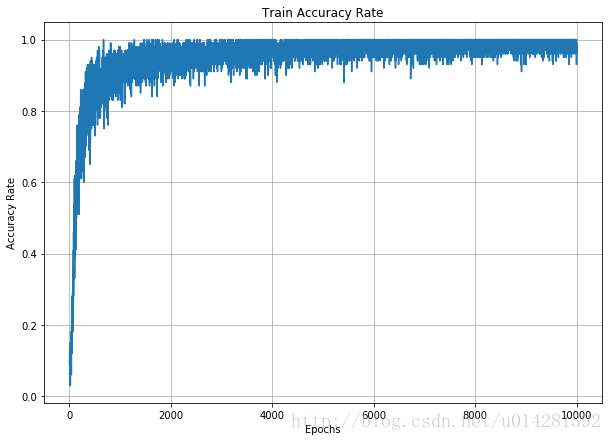
    # 準確率曲線
    fig7,ax7 = plt.subplots(figsize=(10,7))
    plt.plot(Accuracy)
    ax7.set_xlabel('Epochs')
    ax7.set_ylabel('Accuracy Rate')
    plt.title('Train Accuracy Rate')
    plt.grid()
    plt.show()
#----------------------------------各個層特徵視覺化-------------------------------
    # imput image
    fig2,ax2 = plt.subplots(figsize=(2,2))
    ax2.imshow(np.reshape(mnist.train.images[11], (28, 28)))
    plt.show()

    # 第一層的卷積輸出的特徵圖
    input_image = mnist.train.images[11:12]
    conv1_16 = sess.run(h_conv1, feed_dict={x:input_image})     # [1, 28, 28 ,16] 
    conv1_transpose = sess.run(tf.transpose(conv1_16, [3, 0, 1, 2]))
    fig3,ax3 = plt.subplots(nrows=1, ncols=16, figsize = (16,1))
    for i in range(16):
        ax3[i].imshow(conv1_transpose[i][0])                      # tensor的切片[row, column]

    plt.title('Conv1 16x28x28')
    plt.show()

    # 第一層池化後的特徵圖
    pool1_16 = sess.run(h_pool1, feed_dict={x:input_image})     # [1, 14, 14, 16]
    pool1_transpose = sess.run(tf.transpose(pool1_16, [3, 0, 1, 2]))
    fig4,ax4 = plt.subplots(nrows=1, ncols=16, figsize=(16,1))
    for i in range(16):
        ax4[i].imshow(pool1_transpose[i][0])

    plt.title('Pool1 16x14x14')
    plt.show()

    # 第二層卷積輸出特徵圖
    conv2_32 = sess.run(h_conv2, feed_dict={x:input_image})          # [1, 14, 14, 32]
    conv2_transpose = sess.run(tf.transpose(conv2_32, [3, 0, 1, 2]))
    fig5,ax5 = plt.subplots(nrows=1, ncols=32, figsize = (32, 1))
    for i in range(32):
        ax5[i].imshow(conv2_transpose[i][0])
    plt.title('Conv2 32x14x14')
    plt.show()

    # 第二層池化後的特徵圖
    pool2_32 = sess.run(h_pool2, feed_dict={x:input_image})         #[1, 7, 7, 32]
    pool2_transpose = sess.run(tf.transpose(pool2_32, [3, 0, 1, 2]))
    fig6,ax6 = plt.subplots(nrows=1, ncols=32, figsize = (32, 1))
    plt.title('Pool2 32x7x7')
    for i in range(32):
        ax6[i].imshow(pool2_transpose[i][0])

    plt.show()

Epoch : 1 ,  Cost : 1.7629557
Epoch : 2 ,  Cost : 0.8955871
Epoch : 3 ,  Cost : 0.6002768
Epoch : 4 ,  Cost : 0.4222347
Epoch : 5 ,  Cost : 0.4106165
Epoch : 6 ,  Cost : 0.5070749
Epoch : 7 ,  Cost : 0.5032627
Epoch : 8 ,  Cost : 0.3399751
Epoch : 9 ,  Cost : 0.1524799
Epoch : 10 ,  Cost : 0.2328545
Epoch : 11 ,  Cost : 0.1815660
Epoch : 12 ,  Cost : 0.2749544
Epoch : 13 ,  Cost : 0.2539429
Epoch : 14 ,  Cost : 0.1850740
Epoch : 15 ,  Cost : 0.3227096
Epoch : 16 ,  Cost : 0.0711472
Epoch : 17 ,  Cost : 0.1688010
Epoch : 18 ,  Cost : 0.1442217
Epoch : 19 ,  Cost : 0.2415594
Epoch : 20 ,  Cost : 0.0848383
Epoch : 21 ,  Cost : 0.1879225
Epoch : 22 ,  Cost : 0.1355369
Epoch : 23 ,  Cost : 0.1578972
Epoch : 24 ,  Cost : 0.1017473
Epoch : 25 ,  Cost : 0.2265745
Epoch : 26 ,  Cost : 0.2625684
Epoch : 27 ,  Cost : 0.1950202
Epoch : 28 ,  Cost : 0.0607868
Epoch : 29 ,  Cost : 0.0782418
Epoch : 30 ,  Cost : 0.0744723
Epoch : 31 ,  Cost : 0.0848689
Epoch : 32 ,  Cost : 0.1038134
Epoch : 33 ,  Cost : 0.0848786
Epoch : 34 ,  Cost : 0.1219746
Epoch : 35 ,  Cost : 0.0889094
Epoch : 36 ,  Cost : 0.0605406
Epoch : 37 ,  Cost : 0.0478896
Epoch : 38 ,  Cost : 0.1100840
Epoch : 39 ,  Cost : 0.0168766
Epoch : 40 ,  Cost : 0.0479708
Epoch : 41 ,  Cost : 0.1187883
Epoch : 42 ,  Cost : 0.0707371
Epoch : 43 ,  Cost : 0.0471128
Epoch : 44 ,  Cost : 0.1206998
Epoch : 45 ,  Cost : 0.0674985
Epoch : 46 ,  Cost : 0.1218394
Epoch : 47 ,  Cost : 0.0840694
Epoch : 48 ,  Cost : 0.0468497
Epoch : 49 ,  Cost : 0.0899443
Epoch : 50 ,  Cost : 0.0111846
Epoch : 51 ,  Cost : 0.0653627
Epoch : 52 ,  Cost : 0.1446207
Epoch : 53 ,  Cost : 0.0320902
Epoch : 54 ,  Cost : 0.0792156
Epoch : 55 ,  Cost : 0.1250363
Epoch : 56 ,  Cost : 0.0477339
Epoch : 57 ,  Cost : 0.0249218
Epoch : 58 ,  Cost : 0.0571465
Epoch : 59 ,  Cost : 0.0152223
Epoch : 60 ,  Cost : 0.0373616
Epoch : 61 ,  Cost : 0.0417238
Epoch : 62 ,  Cost : 0.0710011
Epoch : 63 ,  Cost : 0.0654174
Epoch : 64 ,  Cost : 0.0234730
Epoch : 65 ,  Cost : 0.0267291
Epoch : 66 ,  Cost : 0.0329132
Epoch : 67 ,  Cost : 0.0344089
Epoch : 68 ,  Cost : 0.1151591
Epoch : 69 ,  Cost : 0.0555586
Epoch : 70 ,  Cost : 0.0213475
Epoch : 71 ,  Cost : 0.0567649
Epoch : 72 ,  Cost : 0.1207196
Epoch : 73 ,  Cost : 0.0407380
Epoch : 74 ,  Cost : 0.0580697
Epoch : 75 ,  Cost : 0.0352901
Epoch : 76 ,  Cost : 0.0420529
Epoch : 77 ,  Cost : 0.0016548
Epoch : 78 ,  Cost : 0.0184542
Epoch : 79 ,  Cost : 0.0657262
Epoch : 80 ,  Cost : 0.0185127
Epoch : 81 ,  Cost : 0.0211956
Epoch : 82 ,  Cost : 0.0709701
Epoch : 83 ,  Cost : 0.1013358
Epoch : 84 ,  Cost : 0.0876017
Epoch : 85 ,  Cost : 0.1351897
Epoch : 86 ,  Cost : 0.1239478
Epoch : 87 ,  Cost : 0.0147001
Epoch : 88 ,  Cost : 0.0155131
Epoch : 89 ,  Cost : 0.0425102
Epoch : 90 ,  Cost : 0.0912542
Epoch : 91 ,  Cost : 0.0445287
Epoch : 92 ,  Cost : 0.0823120
Epoch : 93 ,  Cost : 0.0155016
Epoch : 94 ,  Cost : 0.0869377
Epoch : 95 ,  Cost : 0.0641734
Epoch : 96 ,  Cost : 0.0498264
Epoch : 97 ,  Cost : 0.0289681
Epoch : 98 ,  Cost : 0.0271511
Epoch : 99 ,  Cost : 0.0131940
Epoch : 100 ,  Cost : 0.0418167
training finished

訓練交叉熵代價
這裡寫圖片描述