HDU 3068 最長迴文 manacher演算法
阿新 • • 發佈:2019-01-24
Manacher演算法的裸題
下面簡單說一下複雜度為O(n)的馬拉車演算法
首先過程中涉及到的變數有:
p[i]表示以t[i]字元為中心的迴文子串的半徑
id為最大回文子串中心的位置
mx是迴文串能延伸到的最右端的位置
通過p陣列我們就可以找到最長迴文子串及其位置,,那麼下面我們就來看如何求p陣列
這裡有一個非常神奇的東西
p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1;- 1
慢慢理解它……
這一行程式碼相當於
如果mx > i, 則 p[i] = min(p[2 * id - i], mx - i)
否則, p[i] = 1
看圖說話 
第一種情況
1.如果j點的迴文串沒有超出mx的對稱點,那麼i點的迴文串應該和j一樣,如上圖,即p【i】=p【j】;
2.如果j點的迴文串超出了mx的對稱點,那麼只能保證i在mx前是迴文的,即以i為中心,mx-i為半徑以內是迴文的,如下圖,即p【i】=mx-i;
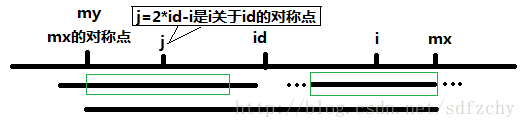
然後再一步步對下一位進行比較;
第二種情況,i在mx外,就只能一步步比較了;
至此,核心內容就說完了
但這還是不夠的
為什麼呢?
顯然(真的是顯然嗎?)
上面的東東只能搞出迴文串長度是奇數的情況,即有一個對稱中心,比如aba
但迴文串長度是偶數怎麼辦呢,比如abba
不要方
加一個預處理
在原字串的每兩個字元間插入一個“#”
實際上對於求迴文串是沒有影響的(非常科學)
為了防止越界,還要在最前面加一個其他神奇的字元,比如“¥”
然後就是這樣
bob –> ¥#b#o#b#
noon –> ¥#n#o#o#n#
這樣做的好處是不論原字串是奇數還是偶數個,處理之後得到的迴文串的個長度都是奇數(雖然長得很醜)
HDU 3068 最長迴文
Problem Description給出一個只由小寫英文字元a,b,c...y,z組成的字串S,求S中最長迴文串的長度.迴文就是正反讀都是一樣的字串,如aba, abba等Input輸入有多組case,不超過120組,每組輸入為一行小寫英文字元a,b,c...y,z組成的字串S
兩組case之間由空行隔開(該空行不用處理)
字串長度len <= 110000Output每一行一個整數x,對應一組case,表示該組case的字串中所包含的最長迴文長度.
Sample Inputaaaaabab
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
char a[300010], b[300010];
int p[300010];
int manacher() {
int ans = 0;
b[0] = '$';
b[1] = '#';
int len = strlen(a);
for(int i = 1; i <= len; i++) {
b[2*i] = a[i-1];
b[2*i+1] = '#';
}
len = len*2 + 2;
int mx = 0, id = 0;
for(int i = 1; i < len; i++) {
p[i] = mx > i? min(p[2*id-i], mx-i):1;
while(b[i+p[i]] == b[i-p[i]]) p[i]++;
p[i]--;
if(i+p[i] > mx) {
mx = i + p[i];
id = i;
}
ans = max(ans, p[i]);
}
return ans;
}
int main() {
while(scanf("%s", a) != EOF) {
printf("%d\n", manacher());
}
return 0;
}