快速排序是排序演算法中效率相對較高的，但使用的人卻是比較少，大家一般信手拈來的排序演算法就是氣泡排序。因為氣泡排序主觀，容易理解，而快速排序使用到了遞迴，大家可能就有點不知所措了。

演算法分析

        快速排序由C. A. R. Hoare在1962年提出。它的基本思想是：通過一趟排序將要排序的資料分割成獨立的兩部分，其中一部分的所有資料都比另外一部分的所有資料都要小，然後再按此方法對這兩部分資料分別進行快速排序，整個排序過程可以遞迴進行，以此達到整個資料變成有序序列。

        我看了下網上有些bolg寫排序演算法，有的是理解錯誤了；有的呢是太過於複雜；還有的呢就乾脆是用臨時陣列，而不是就地排序。當然我的也並沒有多好，只是提夠一種思路；

       說說我的基本思路：每次都取陣列的第一個元素作為比較標準（哨兵元素），凡是大於這個哨兵元素的都放在它的右邊，凡是小於這個哨兵元素的都放在它的左邊；

        大概的步驟：

        1、判斷引數條件，其實這是遞迴的出口；

2、以陣列的第一個元素為哨兵元素，讓其他元素和它比較大小；(記住這時候第一個元素位置是口的，因為裡面的值被作為哨兵元素儲存起來了)

 3、開始從陣列尾部往前迴圈得到一個小於哨兵元素的  元素A ，把該  元素A  放到第一個元素位置（也就是哨兵元素位置上，因為哨兵元素位置是空的）；（這時候要記住 元素A  的位置是空的了）

4、開始從陣列頭部往後迴圈得到一個大於哨兵元素的   元素B ，把該  元素B  放在上一步中移出的  元素A  的位置上；

5、依次迴圈上面3、4步，直到最後一個元素為止，那麼最後一個元素就存放哨兵元素了。

6、把小於哨兵元素的那一部分和大於哨兵元素的那一部分分別遞迴呼叫本函式，依次遞迴排序好所有元素；

實現程式碼

        程式碼部分：    

1. #include<stdio.h>
2. // 列印陣列
3.  void print_array(int *array, int length)  
4.  {  
5.      int index = 0;  
6.      printf("array:\n");  
7.      for(; index < length; index++){  
8.          printf(" %d,"
   , *(array+index));  
9.      }     
10.      printf("\n\n");  
11.  }  
12.  void quickSort(int array[], int length)  
13.  {  
14.      int start = 0;  
15.      int end = length-1;  
16.      int value = array[start];// 得到哨兵元素
17.      if (1 > length) return;// 遞迴出口
18.      while(start < end){// 以哨兵元素為標準，分成大於它和小於它的兩列元素
19.          while(start < end){// 從陣列尾部往前迴圈得到小於哨兵元素的一個元素
20.              if ( array[end--] < value ){  
21.                  array[start++] = array[++end];  
22.                  break;  
23.              }     
24.          }     
25.          while( start < end ){// 從陣列頭部往後迴圈得到大於哨兵元素的一個元素
26.              if( array[start++] > value){  
27.                  array[end--] = array[--start];  
28.                  break;  
29.              }     
30.          }     
31.      }     
32.      array[start] = value;// 放置哨兵元素
33.      printf("\nstart:%d, end:%d\n", start, end);// 這個是測試下start和end是否一樣
34.      quickSort(array, start);// 遞迴排序小於哨兵元素的那一列元素
35.      quickSort(array + start + 1, length - start - 1);// 遞迴排序大於哨兵元素的那一列
36.  }  
37.  int main(void)  
38.  {  
39.      int array[12] = {1,11,12,4,2,6,9,0,3,7,8,2};  
40.      print_array(array, 12);// 開始前列印下
41.      quickSort(array, 12);// 快速排序
42.      print_array(array, 12);// 排序後列印下
43.      return 0;  
44.  }  

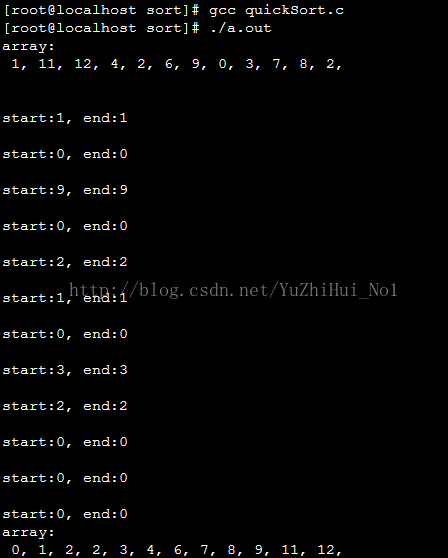
        執行結果：

        

時間複雜度

        快速排序涉及到遞迴呼叫，所以該演算法的時間複雜度還需要從遞迴演算法的複雜度開始說起；        遞迴演算法的時間複雜度公式：T[n] = aT[n/b] + f(n)  ；對於遞迴演算法的時間複雜度這裡就不展開來說了；

最優情況下時間複雜度

        快速排序最優的情況就是每一次取到的元素都剛好平分整個陣列(很顯然我上面的不是)；         此時的時間複雜度公式則為：T[n] = 2T[n/2] + f(n)；T[n/2]為平分後的子陣列的時間複雜度，f[n] 為平分這個陣列時所花的時間；         下面來推算下，在最優的情況下快速排序時間複雜度的計算(用迭代法)：                                          T[n] =  2T[n/2] + n                                                                     ----------------第一次遞迴

                 令：n = n/2        =  2 { 2 T[n/4] + (n/2) }  + n                                               ----------------第二次遞迴

                                            =  2^2 T[ n/ (2^2) ] + 2n

                令：n = n/(2^2)   =  2^2  {  2 T[n/ (2^3) ]  + n/(2^2)}  +  2n                         ----------------第三次遞迴  

                                            =  2^3 T[  n/ (2^3) ]  + 3n

                ......................................................................................                        

                令：n = n/(  2^(m-1) )    =  2^m T[1]  + mn                                                  ----------------第m次遞迴(m次後結束)

               當最後平分的不能再平分時，也就是說把公式一直往下跌倒，到最後得到T[1]時，說明這個公式已經迭代完了（T[1]是常量了）。

               得到：T[n/ (2^m) ]  =  T[1]    ===>>   n = 2^m   ====>> m = logn；

               T[n] = 2^m T[1] + mn ；其中m = logn;

               T[n] = 2^(logn) T[1] + nlogn  =  n T[1] + nlogn  =  n + nlogn  ；其中n為元素個數

               又因為當n >=  2時：nlogn  >=  n  (也就是logn > 1)，所以取後面的 nlogn；

               綜上所述：快速排序最優的情況下時間複雜度為：O( nlogn )

最差情況下時間複雜度

        最差的情況就是每一次取到的元素就是陣列中最小/最大的，這種情況其實就是氣泡排序了(每一次都排好一個元素的順序)

     這種情況時間複雜度就好計算了，就是氣泡排序的時間複雜度：T[n] = n * (n-1) = n^2 + n;

     綜上所述：快速排序最差的情況下時間複雜度為：O( n^2 )

平均時間複雜度

       快速排序的平均時間複雜度也是：O(nlogn)

空間複雜度

        其實這個空間複雜度不太好計算，因為有的人使用的是非就地排序，那樣就不好計算了（因為有的人用到了輔助陣列，所以這就要計算到你的元素個數了）；我就分析下就地快速排序的空間複雜度吧；         首先就地快速排序使用的空間是O(1)的，也就是個常數級；而真正消耗空間的就是遞迴呼叫了，因為每次遞迴就要保持一些資料；      最優的情況下空間複雜度為：O(logn)  ；每一次都平分陣列的情況      最差的情況下空間複雜度為：O( n )      ；退化為氣泡排序的情況         還有個問題就是怎麼取哨兵元素才能不會讓這個演算法退化到氣泡排序，想想了還是算了吧，越深入研究就會有越多感興趣的問題，而我又不是搞演算法分析的，所以就先這樣吧。