MATLAB中向量場圖的繪製 (quiver/quiver3/dfield/pplane) Plot the vector field with MATLAB
一般用於繪製二維向量場圖,函式呼叫方法如下:
|
1 |
|
該函式展示了點(x,y)對應的的向量(u,v)。其中,x的長度要求等於u、v的列數,y的長度要求等於u、v的行數。在繪製圖像的過程中,通常用 meshgrid 來生成所需的網格取樣點。
下面舉幾個例子:
例1:一個最簡單的例子,該二維向量場圖中的向量皆從(0,0)出發,分別指向(1,0) 、(-1,0) 、(0,1) 、(0,-1)。
|
1 2 3 4 5 |
|
畫出下圖
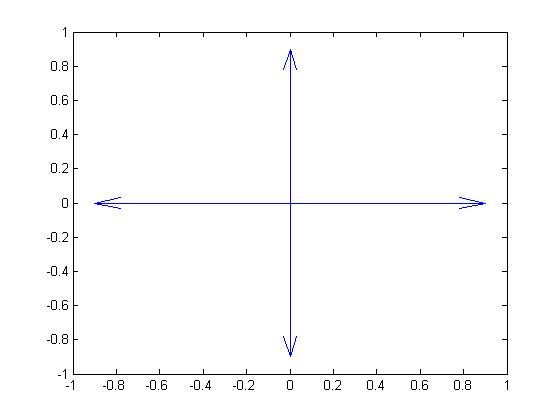
但我們發現箭頭並沒有完全指到(1,0) 、(-1,0) 、(0,1) 、(0,-1) 。如果需要箭頭完全指到(1,0) 、(-1,0) 、(0,1) 、(0,-1),我們需要改變scale引數,將其設為1。參考方法如下:
|
1 |
|
畫出影象如下 :
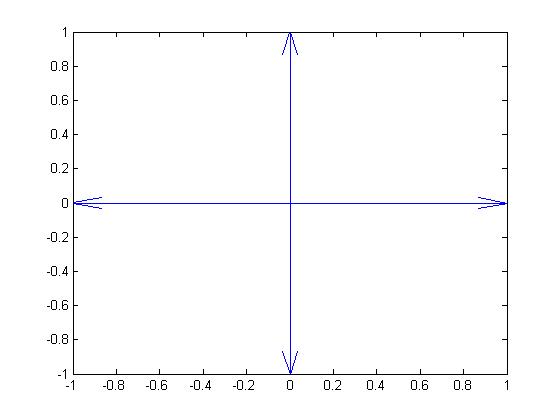
當然,也可以改變顏色。改變顏色可以參考LineSpec的設定,參考程式碼如下:
|
1 |
%這裡將影象設定為紅色
|
畫出影象如下:

例2:(參考MathWorks):已知u=ycosxu=ycosx, v=ysinxv=ysinx
|
1 2 3 4 |
|
畫出下圖:
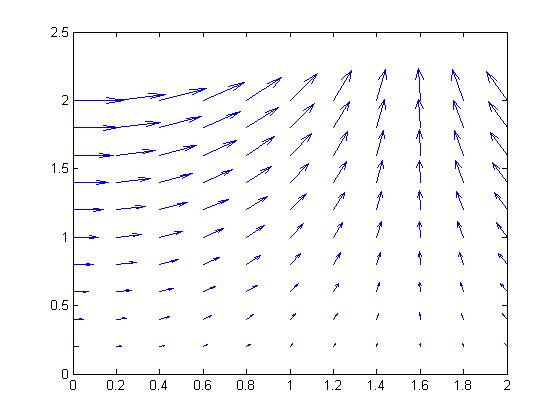
用法與quiver類似,用於三維向量場圖的繪製。
例3: (參考MathWorks
|
1 2 3 4 |
|
畫出下圖:
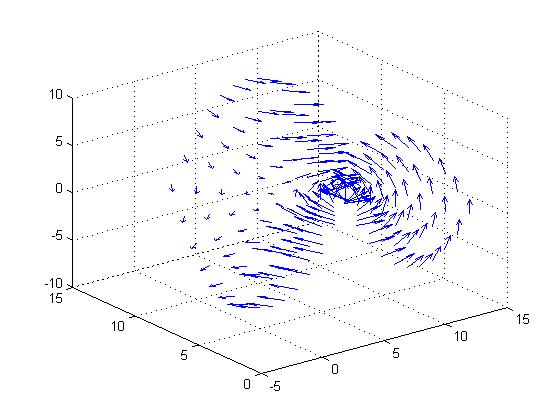
3.dfield與pplane(多應用於常微分方程)
dfield與pplane的原作者是Rice University的John C. Polking,用於解決涉及常微分方程的問題,比較方便,這裡可以下載dfield與pplane的.m檔案
在MATLAB中呼叫dfield,呈現 :
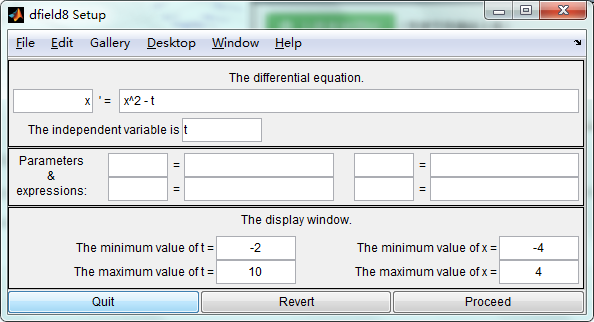
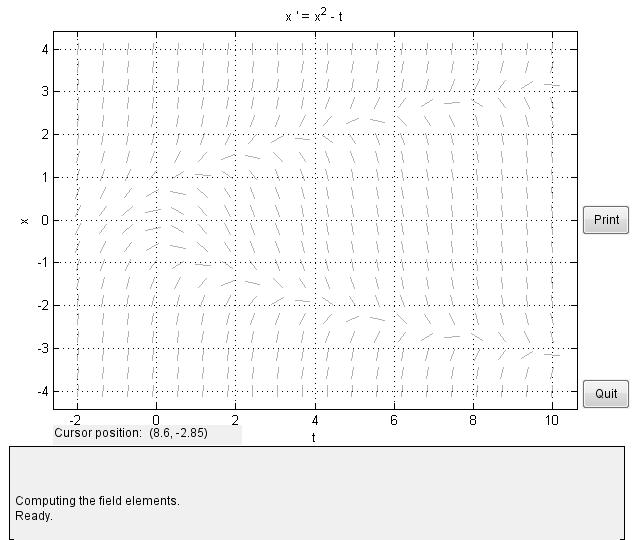
如果我們要繪製常微分方程x′=x2−tx′=x2−t對應的向量場圖,我們可以輸入對應的公式與引數值。在這裡,上圖中預設的常微分方程對應向量場圖:
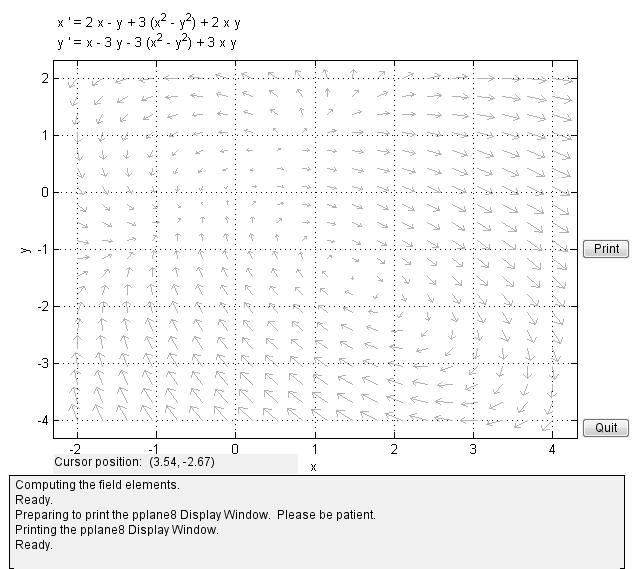
在MATLAB中呼叫pplane,呈現

以預設的微分方程為例,可以繪製向量場圖: