Neural Networks and Deep Learning學習筆記ch1
最近開始看一些深度學習的資料,想學習一下深度學習的基礎知識。找到了一個比較好的tutorial,Neural Networks and Deep Learning,認真看完了之後覺得收穫還是很多的。從最基本的感知機開始講起,到後來使用logistic函式作為啟用函式的sigmoid neuron,和很多其他現在深度學習中常使用的trick。把深度學習的一個發展過程講得很清楚,而且還有很多原始碼和實驗幫助理解。看完了整個tutorial後打算再重新梳理一遍,來寫點總結,以後再看其他資料了可以來更新,查漏補缺,溫故而知新。
- 感知機
- Sigmoid神經元
- 神經網路的結構
- 用梯度下降法來學習
- 參考
感知機-Perceptron
在講神經網路之前,不得不提感知機。感知機在1950s和1960s由Frank Rosenblatt提出,是一種人為設計的neuron, 不過現在在神經網路中通常使用sigmoid neuron,但還是有必要了解一下感知機。
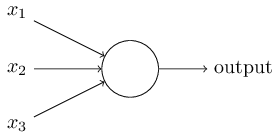
在上面這個例子中是一個感知機神經元,有三個輸入
有上面的公式可以很容易地看出來感知機是怎麼工作的。
但是可以看出,感知機的輸出只有 0 和 1,導致了感知機有一定的侷限性,這讓感知機看起來就只是簡單的邏輯閘,而且還不能通過感知機構造出異或門。
Sigmoid神經元-Sigmoid neurons
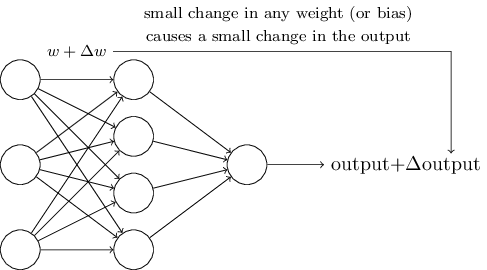
如上所示為一個神經網路,如果權重的微小變化能夠讓輸出也相應有一個比較小的變化,那麼就可以讓這個神經網路做一個稍微複雜一點的工作了。而之前的感知機的輸出是二值的,只有在閾值附近,輸入的變化才可能導致神經元的輸出變化,而且還是突變,這樣一個神經網路就是有點數字化了的感覺,本科學的數位電路就是這樣子的。所以就有人提出一個新的神經元,sigmoid neuron,該神經元使用Sigmoid_function作為啟用函式。sigmoid函式也叫logistic函式,在機器學習中很常見,該函式表示式為
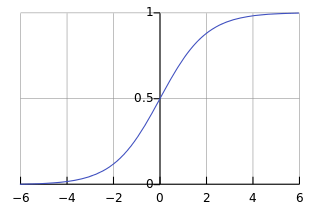
可以看到sigmoid函式的輸出是從 0 到 1 連續變化的,在 0 處函式值為0.5。
令x為神經元的輸入
另外,改變
神經網路的結構-The architecture of neural networks
神經網路通常由輸入層、隱藏層和輸出層組成,輸入輸出都是隻有一層,但隱藏層可以有多層,深度學習中就是通過增加隱藏層的層數來完成一些比較複雜的功能。如下為一個神經網路:
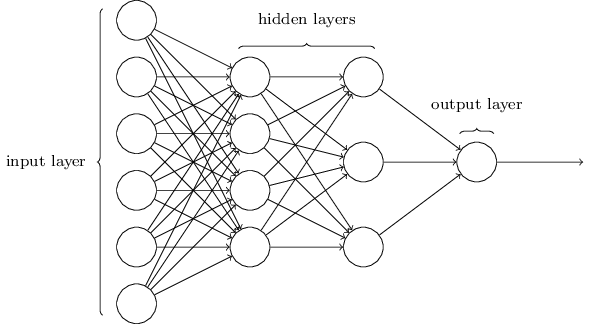
通常情況下,神經網路的每兩個相鄰層之間的神經元都是兩兩相連線的。
用梯度下降法來學習-Learning with gradient descent
建立一個如上所示神經網路之後,需要通過訓練來學習權重
首先要先定義一個代價函式,當預測的輸出和預期的輸出不一致時,就懲罰該函式:
這裡
下一章中詳細介紹神經網路訓練用到的經典的反向傳播演算法。
