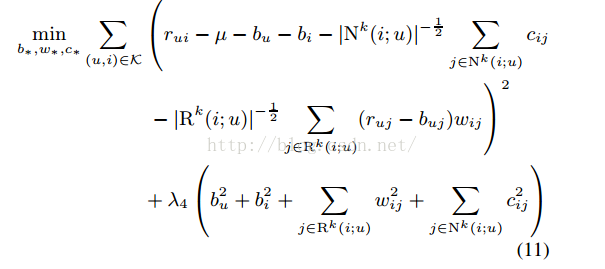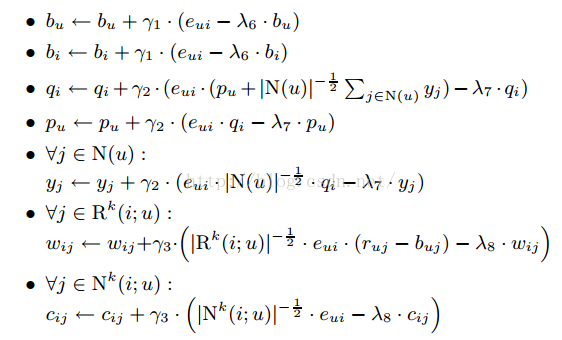基本介紹

伴隨的電商業務蓬勃發展，推薦系統也受到了格外重視，在通常電商系統中都是採用基於CF（Collaborative filtering）演算法原型來做的。該演算法是基於這樣基本假設：people who agreed in the past will agree in the future 。

說到SVD演算法不能不說到Netflix舉辦的推薦大賽，這次比賽對推薦系統工業界產生了很大影響，伴隨著提出了很多演算法思路，所以本文也是以這次比賽為主線，參考其中相關的兩篇經典論文，兩篇文章會上傳。

CF演算法的挑戰：對於每個user ，未知的item 評分會大體上相似，因此對於那些只給少量item有評分的user將會有比較大的預測誤差，因為這樣的user缺乏足夠資訊做預測。

Netflix比賽中最簡單直觀思路就是利用KNN演算法思想，對於某個user 某個未評分的item，找到那個user 近鄰的users，然後多個近鄰user通過相似性加權來預測這個未評分的item，這個思路很簡單實現上也不難，但是這裡有個關鍵問題就是如何計算近鄰，如何定義近鄰的相似性，我們通過計算users 和 objects特徵來計算相似性，但是這個特徵很難去構建好。

另外一種思路：matrix factorization 矩陣分解，這其中最常用的就是Singular Value Decomposition演算法，SVD直接找到每個user和object的特徵，通過user 和object特徵對未評分的item進行評分預測。

SVD

SVD跟別的矩陣分解演算法相比：沒有強加任何限制並且更容易實現

上面是最基本的SVD演算法形態，預測函式p 通常就是用簡單的dot product 運算，我們知道當我們把一個問題損失函式定義好了，下面要做的就是最優化的問題。

這個演算法考慮到評分割槽間問題，需要把預測值限定在指定評分割槽間

對上面損失函式求偏導如公式（5）（6）所示。

Batch learning of SVD

所以整個演算法流程就如下：（Batch learning of SVD）

然後論文中也給出瞭如何給U、V矩陣賦初值的演算法。

公式中a是評分的下界，n(r)是在[-r,r]的均勻分佈，上面提到的SVD演算法是其最標準的形式，但是這個形式不是和大規模並且稀疏的矩陣學習，在這種情況下梯度下降會有很大的方差並且需要一個很小的學習速率防止發散。

前面提到了Batch learning of SVD ，我們會發現一個問題就是：如果評分矩陣V 有一些小的變動，比如某個user增加了評分，這是我們利用Batch learning of SVD 又需要把所有資料學習一次，這會造成很大的計算浪費。

如上所述我們每次針對Ui ：feature vector of user i 進行學習更新

更極端的情況我們可以針對每一個評分來進行學習如下圖：

Incomplete incremental learning of SVD

針對上面基於某個user 學習或者基於某個評分學習演算法我們稱為增量學習（incremental learning）

演算法 2 是基於某個user 的 叫做非完全的增量學習

Complete incremental learning of SVD

演算法 3 是基於某個評分進行更新的演算法，叫做完全增量學習演算法。

演算法3還可以有一些改進提升空間：加入per-user bias and per-object bias

在論文結論部分：batch learning or incomplete incremental learning 需要一個很小的學習速率並且跟 complete incremental learning 相比效能不穩定，所以綜合得出結論就是complete incremental learning 是對於millions 訓練資料最好選擇。

Mahout中SVD實現

在Mahout中也會發現時基於complete incremental learning 演算法進行的實現

 protected void updateParameters(long userID, long itemID, float rating, double currentLearningRate) {
    int userIndex = userIndex(userID);
    int itemIndex = itemIndex(itemID);

    double[] userVector = userVectors[userIndex];
    double[] itemVector = itemVectors[itemIndex];
    double prediction = predictRating(userIndex, itemIndex);
    double err = rating - prediction;

    // adjust user bias
    userVector[USER_BIAS_INDEX] +=
        biasLearningRate * currentLearningRate * (err - biasReg * preventOverfitting * userVector[USER_BIAS_INDEX]);

    // adjust item bias
    itemVector[ITEM_BIAS_INDEX] +=
        biasLearningRate * currentLearningRate * (err - biasReg * preventOverfitting * itemVector[ITEM_BIAS_INDEX]);

    // adjust features
    for (int feature = FEATURE_OFFSET; feature < numFeatures; feature++) {
      double userFeature = userVector[feature];
      double itemFeature = itemVector[feature];

      double deltaUserFeature = err * itemFeature - preventOverfitting * userFeature;
      userVector[feature] += currentLearningRate * deltaUserFeature;

      double deltaItemFeature = err * userFeature - preventOverfitting * itemFeature;
      itemVector[feature] += currentLearningRate * deltaItemFeature;
    }
  }

  private double predictRating(int userID, int itemID) {
    double sum = 0;
    for (int feature = 0; feature < numFeatures; feature++) {
      sum += userVectors[userID][feature] * itemVectors[itemID][feature];
    }
    return sum;
  }

Neflix比賽勝出文章--SVD++

現在工業界通常依賴的是CF協同過濾演算法，協同過濾演算法當中最成功方法有兩個：1. neighborhood models 通過分析商品和users相似性來構建的模型 2. latent factor models 直接構建users and products profile。

Latent factor model：如SVD 通過把items 和users 轉換到latent factor space，因而可以使得items 和 users 直接可以比較。

SVD直觀理解的描述，假設問一個朋友喜歡什麼型別音樂，他列出來了一些藝術家，根據經驗知識我們知道他喜歡是古典音樂和爵士音樂。這種表達不是那麼精確但是也不是太不精確。如果iTunes 進行歌曲推薦是基於數百萬個流派而不是基於數十億歌曲進行推薦，就能執行的更快；而且對於音樂推薦而言效果不會差太多。SVD就是起到了對資料進行提煉的作用，它從原始資料各個物品偏好中提煉出數量較少但更有一般性的特徵。這種思想剛好解決了推薦中如下case：兩個使用者都是汽車愛好者，但是表現喜愛的是不同品牌，如果傳統計算相似性兩個使用者不相似，如果使用SVD就能發現兩者都是汽車愛好者。詳細參考：http://blog.csdn.net/huruzun/article/details/45248997#t1

Netflix 比賽給大家經驗是：neighborhood models 和 Latent factor model各自擅長解決不同層次的資料結構。neighborhood models 擅長解決非常 localized 關係，因此這個模型無法捕捉到使用者資料中微弱的訊號。Latent factor model 擅長全面評估items的聯絡，但是在小的 資料集上不擅長髮現強聯絡，兩者各自擅長某些case，所以自然兩者擅長不同我們想把兩者優勢融合。這篇論文創新是並聯起來兩個演算法在一塊，而不是以前做過先使用某個演算法得到輸出，再在輸出上用另外一個演算法。

上面描述的是一個：Baseline estimates

下面說下一個通常的neighborhood model

上述方法是最經典鄰域模型方法，但是作者提出了不同看法，上面模型在正式模型中不可以調整，相似性衡量阻斷了兩個items，沒有分析整個鄰居集下的資料，當鄰居資訊是缺失時計算會出問題。

現在引數Wij 不在是根據鄰居計算出來的，而是通過資料最優化得到Wij的值。現在理解Wij可以為 baseline estimate 的一個 offsets。

現在預測函式形式：考慮了implicit feedback

考慮正則化項的損失函式：

更新規則也就是簡單梯度下降演算法：

SVD++演算法主體流程：

論文中說到SVD++取得了迄今為止最高的正確率，雖然演算法在解釋性上不夠強大。

下面整合了neighborhood model and 正確率最高的LFM--SVD++

上述演算法一個學習迭代過程：

  @Override
  protected void updateParameters(long userID, long itemID, float rating, double currentLearningRate) {
    int userIndex = userIndex(userID);
    int itemIndex = itemIndex(itemID);

    double[] userVector = p[userIndex];
    double[] itemVector = itemVectors[itemIndex];

    double[] pPlusY = new double[numFeatures];
    for (int i2 : itemsByUser.get(userIndex)) {
      for (int f = FEATURE_OFFSET; f < numFeatures; f++) {
        pPlusY[f] += y[i2][f];
      }
    }
    double denominator = Math.sqrt(itemsByUser.get(userIndex).size());
    for (int feature = 0; feature < pPlusY.length; feature++) {
      pPlusY[feature] = (float) (pPlusY[feature] / denominator + p[userIndex][feature]);
    }

    double prediction = predictRating(pPlusY, itemIndex);
    double err = rating - prediction;
    double normalized_error = err / denominator;

    // adjust user bias
    userVector[USER_BIAS_INDEX] +=
        biasLearningRate * currentLearningRate * (err - biasReg * preventOverfitting * userVector[USER_BIAS_INDEX]);

    // adjust item bias
    itemVector[ITEM_BIAS_INDEX] +=
        biasLearningRate * currentLearningRate * (err - biasReg * preventOverfitting * itemVector[ITEM_BIAS_INDEX]);

    // adjust features
    for (int feature = FEATURE_OFFSET; feature < numFeatures; feature++) {
      double pF = userVector[feature];
      double iF = itemVector[feature];

      double deltaU = err * iF - preventOverfitting * pF;
      userVector[feature] += currentLearningRate * deltaU;

      double deltaI = err * pPlusY[feature] - preventOverfitting * iF;
      itemVector[feature] += currentLearningRate * deltaI;

      double commonUpdate = normalized_error * iF;
      for (int itemIndex2 : itemsByUser.get(userIndex)) {
        double deltaI2 = commonUpdate - preventOverfitting * y[itemIndex2][feature];
        y[itemIndex2][feature] += learningRate * deltaI2;
      }
    }
  }

  private double predictRating(double[] userVector, int itemID) {
    double sum = 0;
    for (int feature = 0; feature < numFeatures; feature++) {
      sum += userVector[feature] * itemVectors[itemID][feature];
    }
    return sum;
  }