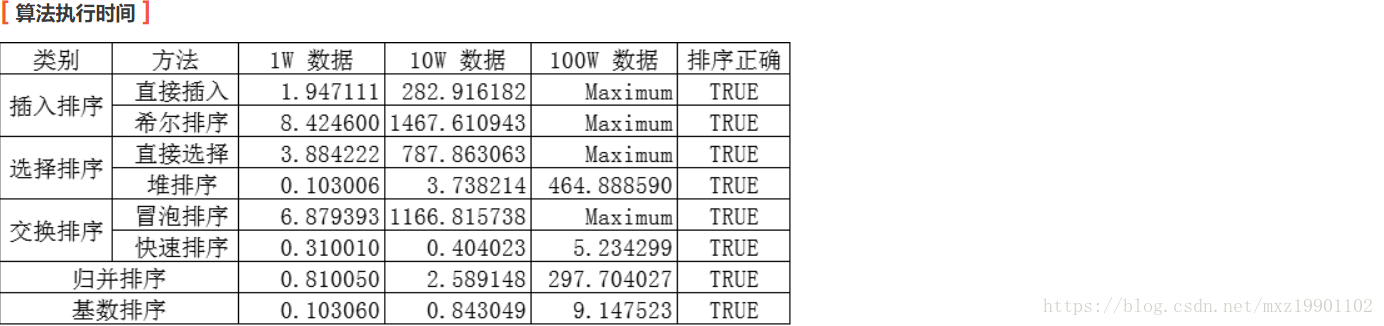
Python八大排序演算法
阿新 • • 發佈:2019-01-25
1.插入排序:插入排序的基本操作就是將一個數據插入到已經排好序的有序資料中,從而得到一個新的、個數加一的有序資料,演算法適用於少量資料的排序;首先將第一個作為已經排好序的,然後每次從後的取出插入到前面並排序;
- 時間複雜度:O(n²)
- 空間複雜度:O(1)
- 穩定性:穩定
def insert_sort(ilist): for i in range(len(ilist)): for j in range(i): if ilist[i] < ilist[j]: ilist.insert(j, ilist.pop(i)) break return ilist ilist = insert_sort([4,5,6,7,3,2,6,9,8]) print ilist
2.希爾排序:希爾排序是把記錄按下標的一定增量分組,對每組使用直接插入排序演算法排序;隨著增量逐漸減少,每組包含的關鍵詞越來越多,當增量減至1時,整個檔案恰被分成一組,演算法便終止
- 時間複雜度:O(n)
- 空間複雜度:O(n√n)
- 穩定性:不穩定
def shell_sort(slist): gap = len(slist) while gap > 1: gap = gap // 2 for i in range(gap, len(slist)): for j in range(i % gap, i, gap): if slist[i] < slist[j]: slist[i], slist[j] = slist[j], slist[i] return slist slist = shell_sort([4,5,6,7,3,2,6,9,8]) print slist
3.氣泡排序:它重複地走訪過要排序的數列,一次比較兩個元素,如果他們的順序錯誤就把他們交換過來。走訪數列的工作是重複地進行直到沒有再需要交換,也就是說該數列已經排序完成
- 時間複雜度:O(n²)
- 空間複雜度:O(1)
- 穩定性:穩定
def bubble_sort(blist): count = len(blist) for i in range(0, count): for j in range(i + 1, count): if blist[i] > blist[j]: blist[i], blist[j] = blist[j], blist[i] return blist blist = bubble_sort([4,5,6,7,3,2,6,9,8]) print blist
4.快速排序:通過一趟排序將要排序的資料分割成獨立的兩部分,其中一部分的所有資料都比另外一部分的所有資料都要小,然後再按此方法對這兩部分資料分別進行快速排序,整個排序過程可以遞迴進行,以此達到整個資料變成有序序列
- 時間複雜度:O(nlog₂n)
- 空間複雜度:O(nlog₂n)
- 穩定性:不穩定
def quick_sort(qlist):
if qlist == []:
return []
else:
qfirst = qlist[0]
qless = quick_sort([l for l in qlist[1:] if l < qfirst])
qmore = quick_sort([m for m in qlist[1:] if m >= qfirst])
return qless + [qfirst] + qmore
qlist = quick_sort([4,5,6,7,3,2,6,9,8])
print qlist5.選擇排序:第1趟,在待排序記錄r1 ~ r[n]中選出最小的記錄,將它與r1交換;第2趟,在待排序記錄r2 ~ r[n]中選出最小的記錄,將它與r2交換;以此類推,第i趟在待排序記錄r[i] ~ r[n]中選出最小的記錄,將它與r[i]交換,使有序序列不斷增長直到全部排序完畢
- 時間複雜度:O(n²)
- 空間複雜度:O(1)
- 穩定性:不穩定
def select_sort(slist):
for i in range(len(slist)):
x = i
for j in range(i, len(slist)):
if slist[j] < slist[x]:
x = j
slist[i], slist[x] = slist[x], slist[i]
return slist
slist = select_sort([4,5,6,7,3,2,6,9,8])
print slist6.堆排序:它是選擇排序的一種。可以利用陣列的特點快速定位指定索引的元素。堆分為大根堆和小根堆,是完全二叉樹。大根堆的要求是每個節點的值都不大於其父節點的值,即A[PARENT[i]] >= A[i]。在陣列的非降序排序中,需要使用的就是大根堆,因為根據大根堆的要求可知,最大的值一定在堆頂
- 時間複雜度:O(nlog₂n)
- 空間複雜度:O(1)
- 穩定性:不穩定
import copy
def heap_sort(hlist):
def heap_adjust(parent):
child = 2 * parent + 1 # left child
while child < len(heap):
if child + 1 < len(heap):
if heap[child + 1] > heap[child]:
child += 1 # right child
if heap[parent] >= heap[child]:
break
heap[parent], heap[child] = heap[child], heap[parent]
parent, child = child, 2 * child + 1
heap, hlist = copy.copy(hlist), []
for i in range(len(heap) // 2, -1, -1):
heap_adjust(i)
while len(heap) != 0:
heap[0], heap[-1] = heap[-1], heap[0]
hlist.insert(0, heap.pop())
heap_adjust(0)
return hlist
hlist = heap_sort([4,5,6,7,3,2,6,9,8])
print hlist7.基數排序:透過鍵值的部份資訊,將要排序的元素分配至某些“桶”中,藉以達到排序的作用
- 時間複雜度:O(d(r+n))
- 空間複雜度:O(rd+n)
- 穩定性:穩定
def radix_sort(array):
bucket, digit = [[]], 0
while len(bucket[0]) != len(array):
bucket = [[], [], [], [], [], [], [], [], [], []]
for i in range(len(array)):
num = (array[i] // 10 ** digit) % 10
bucket[num].append(array[i])
array.clear()
for i in range(len(bucket)):
array += bucket[i]
digit += 1
return array8.歸併排序:採用分治法(Divide and Conquer)的一個非常典型的應用。將已有序的子序列合併,得到完全有序的序列;即先使每個子序列有序,再使子序列段間有序。若將兩個有序表合併成一個有序表,稱為二路歸併
- 時間複雜度:O(nlog₂n)
- 空間複雜度:O(1)
- 穩定性:穩定
def merge_sort(array):
def merge_arr(arr_l, arr_r):
array = []
while len(arr_l) and len(arr_r):
if arr_l[0] <= arr_r[0]:
array.append(arr_l.pop(0))
elif arr_l[0] > arr_r[0]:
array.append(arr_r.pop(0))
if len(arr_l) != 0:
array += arr_l
elif len(arr_r) != 0:
array += arr_r
return array
def recursive(array):
if len(array) == 1:
return array
mid = len(array) // 2
arr_l = recursive(array[:mid])
arr_r = recursive(array[mid:])
return merge_arr(arr_l, arr_r)
return recursive(array)