鄰接矩陣 有向圖 判斷是否有環 是否連通 DFS C實現~
阿新 • • 發佈:2019-01-25
1 DFS 搜尋 修改
有向圖有環需要注意 : 按照路徑方向能組成迴路才叫有環
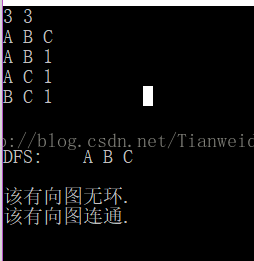
例如 三邊 A->B, A->C, B->C則 構成的不是環
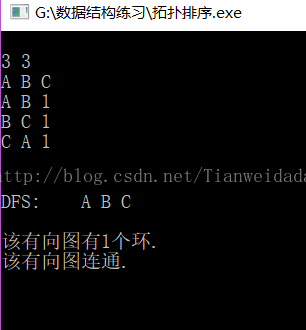
A->B,B->C,C-A 組成的才是環
// 因為是有向圖兩個頂點也可以成環 void dfs(Graph g, int i) { int j; color[i] = gray; //灰色 表示正在訪問 printf("%c ", g.vex[i]); for (j = 0; j < g.vex_num; j++) { if (i != j && g.edge[i][j] != INFINITY) {//兩頂點有邊相連 if (color[j] == white) { dfs(g, j);//如果該節點未訪問 繼續訪問其臨近節點 } else if(color[j] == gray){ loop_num++; is_dag = false; //有環 } } } color[i] = black; } void dfs_trvsal(Graph g) { int i; for (i = 0; i < g.vex_num; i++) { color[i] = white; loop_num = 0; } link_component = 0; for (i = 0; i < g.vex_num; i++) { if (color[i] == white) { link_component++; dfs(g, i); } } }
完整實現 :
#include<stdio.h> #include<stdlib.h> #include<ctype.h> #define MAXVEX 100 #define INFINITY 65535 #define TRUE 1 #define FALSE 0 #define gray -1 #define white 0 #define black 1 int loop_num; //環 數量 int color[MAXVEX]; //-1 表示灰色 0表示白色 1 表示黑色 bool is_dag = true;//是否是有向無環圖 int link_component; // 連通分量 數量 typedef int EdgeType; typedef char VertexType; typedef struct Graph { VertexType vex[MAXVEX]; EdgeType edge[MAXVEX][MAXVEX]; int vex_num, edge_num; }Graph; void init_graph(Graph *g) { int i, j; for (i = 0; i < g->vex_num; i++) { for (j = 0; j < g->vex_num; j++) { if (i == j) { g->edge[i][j] = 0; } else g->edge[i][j] = INFINITY; } } } char read_char() { char ch; do { ch = getchar(); } while (!isalpha(ch)); return ch; } int get_pos(Graph g, char ch) { int i; for (i = 0; i < g.vex_num; i++) { if (g.vex[i] == ch) return i; } return -1; } void create_graph(Graph *g) { int i, k; //printf("請輸入頂點數與邊數:\n"); scanf("%d%d", &g->vex_num, &g->edge_num); init_graph(g);// 初始化 //printf("請輸入頂點資訊:\n"); for (i = 0; i < g->vex_num; i++) { //scanf("%c", g->vex[i]); g->vex[i] = read_char(); } //printf("請輸入邊的資訊:\n"); char c1, c2; int p1, p2,w; for (k = 0; k < g->edge_num; k++) { c1 = read_char(); c2 = read_char(); scanf("%d", &w); p1 = get_pos(*g, c1); p2 = get_pos(*g, c2); g->edge[p1][p2] = w;//有向邊的權重 } } void print_graph(Graph g) { int i, j; for (i = 0; i < g.vex_num; i++) { for (j = 0; j < g.vex_num; j++) { if (g.edge[i][j] == INFINITY) printf("%5c", '*'); else { printf("%5d", g.edge[i][j]); } } printf("\n"); } } // 因為是有向圖兩個頂點也可以成環 void dfs(Graph g, int i) { int j; color[i] = gray; //灰色 表示正在訪問 printf("%c ", g.vex[i]); for (j = 0; j < g.vex_num; j++) { if (i != j && g.edge[i][j] != INFINITY) {//兩頂點有邊相連 if (color[j] == white) { dfs(g, j);//如果該節點未訪問 繼續訪問其臨近節點 } else if(color[j] == gray){ loop_num++; is_dag = false; //有環 } } } color[i] = black; } void dfs_trvsal(Graph g) { int i; for (i = 0; i < g.vex_num; i++) { color[i] = white; loop_num = 0; } link_component = 0; for (i = 0; i < g.vex_num; i++) { if (color[i] == white) { link_component++; dfs(g, i); } } } int main() { Graph g; create_graph(&g); //print_graph(g); printf("\n\nDFS:\t"); dfs_trvsal(g); printf("\n\n"); if (is_dag) { printf("該有向圖無環.\n"); } else { printf("該有向圖有%d個環.\n", loop_num); } if (link_component == 1) { printf("該有向圖連通."); } else { printf("該有向圖不連通."); } getchar(); getchar(); return 0; }