第九屆藍橋杯 螺旋折線
轉自:https://blog.csdn.net/u013377068/article/details/79780383
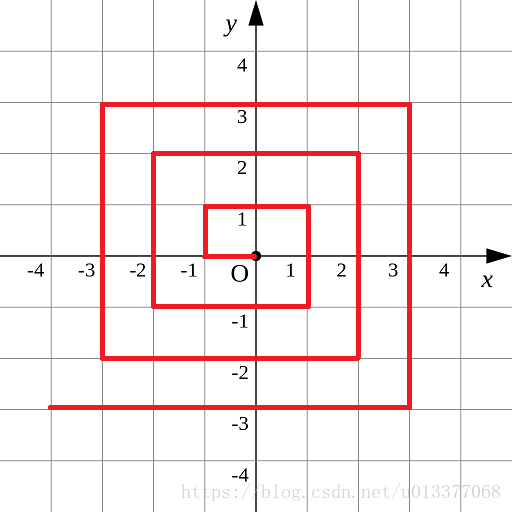
如圖p1.png所示的螺旋折線經過平面上所有整點恰好一次。
對於整點(X, Y),我們定義它到原點的距離dis(X, Y)是從原點到(X, Y)的螺旋折線段的長度。
例如dis(0, 1)=3, dis(-2, -1)=9
給出整點座標(X, Y),你能計算出dis(X, Y)嗎?
【輸入格式】
X和Y
對於40%的資料,-1000 <= X, Y <= 1000
對於70%的資料,-100000 <= X, Y <= 100000
對於100%的資料, -1000000000 <= X, Y <= 1000000000
【輸出格式】
輸出dis(X, Y)
【樣例輸入】
0 1
【樣例輸出】
3
資源約定:
峰值記憶體消耗(含虛擬機器) < 256M
CPU消耗 < 1000ms
請嚴格按要求輸出,不要畫蛇添足地列印類似:“請您輸入...” 的多餘內容。
注意:
main函式需要返回0;
只使用ANSI C/ANSI C++ 標準;
不要呼叫依賴於編譯環境或作業系統的特殊函式。
所有依賴的函式必須明確地在原始檔中 #include <xxx>
不能通過工程設定而省略常用標頭檔案。
提交程式時,注意選擇所期望的語言型別和編譯器型別。
這個是個規律題;
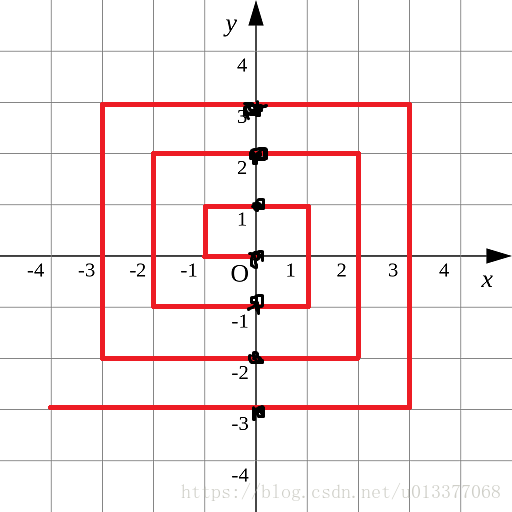
我們觀察圖片可知我們只要找到下面每行的關鍵點的dis就能推出該行的任意一點的dis;
設這些關鍵點為(0,y);
顯然當y > 0,y <= 0兩種不同情況,並且(0,y)的dis跟y有關;
這兩種情況的每個情況又可分為兩種情況。(所以應該是四種情況)。
當y > 0 時:
當abs(x) <= y時,dis(0 , y)=3 * y + (y * y - y) / 2 * 8,所以dis(x , y)=dis(0 , y) + x;
當abs(x) > 時, x > 0時,dis(x , y) = dis(0 , x) + 2 * x - y。
x < 0時,dis(x , y) = dis(0 ,-x) + 2 * x + y。
當y <= 0時:
當y-1 <= x <= -y 時,dis(0 , -y) = 7 * -y + (y * y + y)/2 * 8,所以dis(x , y) =dis(0 , y) - x;
當x >- y 或 x< y - 1時,x > 0 時,dis(x,y) = dis(0 , x) - 2 * x - y。
x < 0 時,dis(x,y) = dis(0 , -x - 1) - 2 * x + y - 1。
可能有人會擔心在這個過程中,資料範圍會超出long long,我來分析一下為什麼不會超出long long。
首先這個過程可能會超出long long也就是 y * y了,題目給的範圍是
-1000000000 <= X, Y <= 1000000000 也就是 -1e9<=x,y<=1e9。
我們來看一下long long的範圍
-9223372036854775808<=long long <=-9223372036854775807,也就是-9e18~9e18。
y * y 最大的值為1e18,小於9e18,而之後乘除操作產生的最大值大約為4e18,至於加減操作
相對於1e18這個數量級其實影響很小。
所以在計算過程中並不會超出long long。
給大家幾組測試資料
輸入
1 0
2 0
3 0
-1 0
-2 0
-3 0
輸出
5 18 39 1 10 27
輸入
1 2
2 2
3 2
-1 2
-2 2
-3 2
輸出
15 16 37 13 12 29
輸入
1 -2
2 -2
3 -2
-1 -2
-2 -2
-3 -2
-4 -2
輸出
21 20 41 23 24 25 50
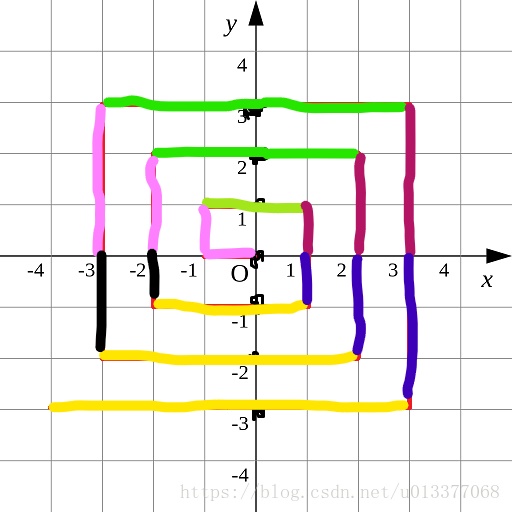
六個表示式計算對應六個顏色的區域,程式碼如下:
#include<stdio.h>
#include<math.h>
#define ll long long
int main()
{
ll x , y;
while(~scanf("%lld %lld",&x, &y))
{
if(y > 0)
{
if(abs(x) <= y)
{
printf("%lld\n",3 * y + (y * y - y) / 2 * 8 + x );//計算綠色區域
}
else
{
if(x > 0)
printf("%lld\n",3 * x + (x * x - x) / 2 * 8 + 2 * x - y);//計算紅色區域
else
printf("%lld\n",3 * -x + (x * x + x) / 2 * 8 + 2 * x + y);//計算粉紅色區域
}
}
else
{
if(y - 1 <= x && x <= -y)
printf("%lld\n",7 * -y + (y * y + y) / 2 * 8 - x);//計算黃色區域
else
{
if(x > 0)
printf("%lld\n",7 * x + (x * x - x)/2 * 8 - 2 * x - y);//計算藍色區域
else
printf("%lld\n",-7 * x - 7 + (x * x + 3 * x + 2)/2 * 8 - 2 * x + y -1);//計算黑色區域
}
}
}
return 0;
}