0 導讀

閱讀本文需要有掌握基本的ARIMA知識，倘若ARIMA相關內容已經遺忘，此處提供以下博文幫你回憶一下：

本文主要分為四個部分：

1.  用pandas處理時序資料
2. 檢驗序資料的穩定性
3. 處理時序資料變成穩定資料
4. 時序資料的預測

和許多時間序列分析一樣，本文同樣使用航空乘客資料（AirPassengers.csv）作為樣例。

1 用pandas匯入和處理時序資料

import numpy as np
import pandas as pd
from datetime import datetime
import matplotlib.pylab as plt

# 讀取資料，pd.read_csv預設生成DataFrame物件，需將其轉換成Series物件
df = pd.read_csv('F:/time/AirPassengers.csv', encoding='utf-8', index_col='TravelDate')
df.index = pd.to_datetime(df.index)  # 將字串索引轉換成時間索引
ts = df['Passengers']  # 生成pd.Series物件
ts.head()
 

執行結果如下：資料包括每個月對應的passenger的數目。

TravelDate
1949-01-01    112
1949-02-01    118
1949-03-01    132
1949-04-01    129
1949-05-01    121
Name: Passengers, dtype: int64

 此時時間為索引

ts.index

結果如下

DatetimeIndex(['1949-01-01', '1949-02-01', '1949-03-01', '1949-04-01',
               '1949-05-01', '1949-06-01', '1949-07-01', '1949-08-01',
               '1949-09-01', '1949-10-01',
               ...
               '1960-03-01', '1960-04-01', '1960-05-01', '1960-06-01',
               '1960-07-01', '1960-08-01', '1960-09-01', '1960-10-01',
               '1960-11-01', '1960-12-01'],
              dtype='datetime64[ns]', name='TravelDate', length=144, freq=None)
 

檢視某日的值既可以使用字串作為索引，又可以直接使用時間物件作為索引

第一種方式

ts['1949-01-01']

112

 第二種方式

ts[datetime(1949,1,1)]

112

如果要檢視某一年的資料，pandas也能非常方便的實現

ts['1949']

TravelDate
1949-01-01    112
1949-02-01    118
1949-03-01    132
1949-04-01    129
1949-05-01    121
1949-06-01    135
1949-07-01    148
1949-08-01    148
1949-09-01    136
1949-10-01    119
1949-11-01    104
1949-12-01    118
Name: Passengers, dtype: int64
 

切片操作：

ts['1949-1' : '1949-6']

TravelDate
1949-01-01    112
1949-02-01    118
1949-03-01    132
1949-04-01    129
1949-05-01    121
1949-06-01    135
Name: Passengers, dtype: int64

2 檢驗序資料的穩定性

因為ARIMA模型要求資料是穩定的，所以這一步至關重要。

1. 判斷資料是穩定的常基於對於時間是常量的幾個統計量：

• 常量的均值
• 常量的方差
• 與時間獨立的自協方差

用影象說明如下：

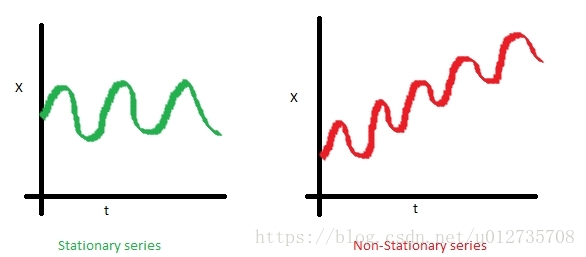
1）均值

X是時序資料的值，t是時間。可以看到左圖，資料的均值對於時間軸來說是常量，即資料的均值不是時間的函式,所有它是穩定的；右圖隨著時間的推移，資料的值整體趨勢是增加的，所有均值是時間的函式，資料具有趨勢，所以是非穩定的。

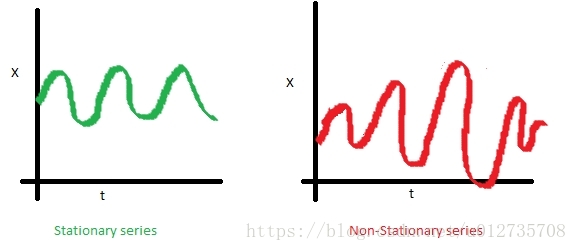
2）方差

可以看到左圖，資料的方差對於時間是常量，即資料的值域圍繞著均值上下波動的振幅是固定的，所以左圖資料是穩定的。而右圖，資料的振幅在不同時間點不同，所以方差對於時間不是獨立的，資料是非穩定的。但是左、右圖的均值是一致的。

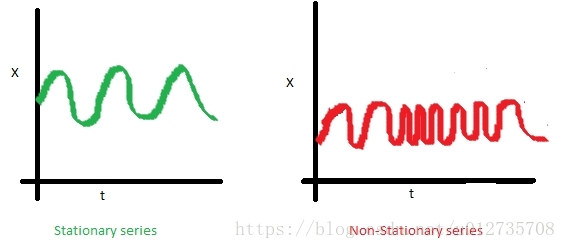
3）自協方差

一個時序資料的自協方差，就是它在不同兩個時刻i,j的值的協方差。可以看到左圖的自協方差於時間無關；而右圖，隨著時間的不同，資料的波動頻率明顯不同，導致它i,j取值不同，就會得到不同的協方差，因此是非穩定的。雖然右圖在均值和方差上都是與時間無關的，但仍是非穩定資料。

2. python判斷時序資料穩定性

平穩性檢驗一般採用觀察法和單位根檢驗法。

觀察法：需計算每個時間段內的平均的資料均值和標準差。

單位根檢驗法：通過Dickey-Fuller Test 進行判斷，大致意思就是在一定置信水平下，對於時序資料假設 Null hypothesis: 非穩定。這是一種常用的單位根檢驗方法，它的原假設為序列具有單位根，即非平穩，對於一個平穩的時序資料，就需要在給定的置信水平上顯著，拒絕原假設。

針對以上兩種方法，進行Python編碼

# 移動平均圖
def draw_trend(timeseries, size):
    f = plt.figure(facecolor='white')
    # 對size個數據進行移動平均
    rol_mean = timeseries.rolling(window=size).mean()
    # 對size個數據移動平均的方差
    rol_std = timeseries.rolling(window=size).std()

    timeseries.plot(color='blue', label='Original')
    rol_mean.plot(color='red', label='Rolling Mean')
    rol_std.plot(color='black', label='Rolling standard deviation')
    plt.legend(loc='best')
    plt.title('Rolling Mean & Standard Deviation')
    plt.show()

def draw_ts(timeseries):
    f = plt.figure(facecolor='white')
    timeseries.plot(color='blue')
    plt.show()

#Dickey-Fuller test:
def teststationarity(ts):
    dftest = adfuller(ts)
    # 對上述函式求得的值進行語義描述
    dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
    for key,value in dftest[4].items():
        dfoutput['Critical Value (%s)'%key] = value
    return dfoutput

檢視原始資料的均值和方差

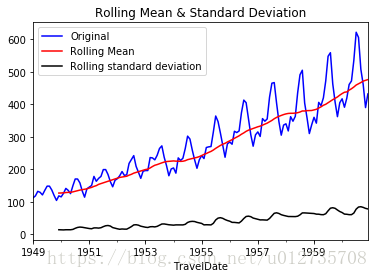
draw_trend(ts,12)

結果如下

通過上圖，我們可以發現數據的移動平均值/標準差有越來越大的趨勢，是不穩定的。接下來我們再看Dickey-Fuller的結果

teststationarity(ts)

結果如下

Test Statistic                   0.815369
p-value                          0.991880
#Lags Used                      13.000000
Number of Observations Used    130.000000
Critical Value (1%)             -3.481682
Critical Value (5%)             -2.884042
Critical Value (10%)            -2.578770
dtype: float64

此時p值為0.991880，說明並不能拒絕原假設。通過DF的資料可以明確的看出，在任何置信度下，資料都不是穩定的。

3 處理時序資料變成穩定資料

資料不穩定的原因主要有以下兩點：

• 趨勢（trend）-資料隨著時間變化。比如說升高或者降低。
• 季節性(seasonality)-資料在特定的時間段內變動。比如說節假日，或者活動導致資料的異常。

由前面的分析可知，該序列是不平穩的，然而平穩性是時間序列分析的前提條件，故我們需要對不平穩的序列進行處理將其轉換成平穩的序列。

1）對數變換

對數變換主要是為了減小資料的振動幅度，使其線性規律更加明顯，同時保留其他資訊。這裡強調一下，變換的序列需要滿足大於0，小於0的資料不存在對數變換。

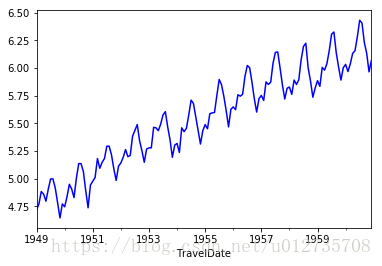
ts_log = np.log(ts)

我們看一下此時的資料分佈

可以看出經過對數變換後，資料值域範圍縮小了，振幅也沒那麼大了。

2）平滑法

根據平滑技術的不同，平滑法具體分為移動平均法和指數平均法。

移動平均即利用一定時間間隔內的平均值作為某一期的估計值，而指數平均則是用變權的方法來計算均值。

移動平均：

def draw_moving(timeSeries, size):
    f = plt.figure(facecolor='white')
    # 對size個數據進行移動平均
    rol_mean = timeSeries.rolling(window=size).mean()
    # 對size個數據進行加權移動平均
    rol_weighted_mean = pd.ewma(timeSeries, span=size)
    #rol_weighted_mean=timeSeries.ewm(halflife=size,min_periods=0,adjust=True,ignore_na=False).mean()

    timeSeries.plot(color='blue', label='Original')
    rol_mean.plot(color='red', label='Rolling Mean')
    rol_weighted_mean.plot(color='black', label='Weighted Rolling Mean')
    plt.legend(loc='best')
    plt.title('Rolling Mean')
    plt.show()
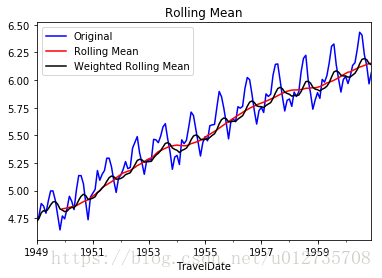
draw_moving(ts_log,12)

結果如下

從上圖可以發現視窗為12的移動平均能較好的剔除年週期性因素，而指數平均法是對週期內的資料進行了加權，能在一定程度上減小年週期因素，但並不能完全剔除，如要完全剔除可以進一步進行差分操作。

3）差分

時間序列最常用來剔除週期性因素的方法當屬差分了，它主要是對等週期間隔的資料進行線性求減。前面我們說過，ARIMA模型相對ARMA模型，僅多了差分操作，ARIMA模型幾乎是所有時間序列軟體都支援的，差分的實現與還原都非常方便。

diff_12 = ts_log.diff(12)
diff_12.dropna(inplace=True)
diff_12_1 = diff_12.diff(1)
diff_12_1.dropna(inplace=True)
teststationarity(diff_12_1)

結果如下

Test Statistic                  -4.443325
p-value                          0.000249
#Lags Used                      12.000000
Number of Observations Used    118.000000
Critical Value (1%)             -3.487022
Critical Value (5%)             -2.886363
Critical Value (10%)            -2.580009
dtype: float64

從上面的統計檢驗結果可以看出，經過12階差分和1階差分後，該序列滿足平穩性的要求了。

4）分解

所謂分解就是將時序資料分離成不同的成分。statsmodels使用的X-11分解過程，它主要將時序資料分離成長期趨勢、季節趨勢和隨機成分。與其它統計軟體一樣，statsmodels也支援兩類分解模型，加法模型和乘法模型，這裡我只實現加法，乘法只需將model的引數設定為"multiplicative"即可。

from statsmodels.tsa.seasonal import seasonal_decompose
def decompose(timeseries):
    
    # 返回包含三個部分 trend（趨勢部分） ， seasonal（季節性部分） 和residual (殘留部分)
    decomposition = seasonal_decompose(timeseries)
    
    trend = decomposition.trend
    seasonal = decomposition.seasonal
    residual = decomposition.resid
    
    plt.subplot(411)
    plt.plot(ts_log, label='Original')
    plt.legend(loc='best')
    plt.subplot(412)
    plt.plot(trend, label='Trend')
    plt.legend(loc='best')
    plt.subplot(413)
    plt.plot(seasonal,label='Seasonality')
    plt.legend(loc='best')
    plt.subplot(414)
    plt.plot(residual, label='Residuals')
    plt.legend(loc='best')
    plt.tight_layout()
    plt.show()
    return trend , seasonal, residual
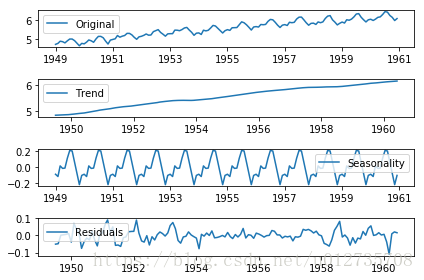
trend , seasonal, residual = decompose(ts_log)
residual.dropna(inplace=True)
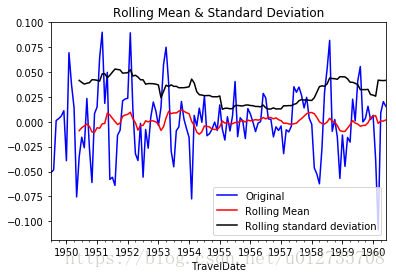
draw_trend(residual,12)
teststationarity(residual)

結果如下

residual的均值、方差以及 DF結果

Test Statistic                -6.332387e+00
p-value                        2.885059e-08
#Lags Used                     9.000000e+00
Number of Observations Used    1.220000e+02
Critical Value (1%)           -3.485122e+00
Critical Value (5%)           -2.885538e+00
Critical Value (10%)          -2.579569e+00
dtype: float64

如圖所示，資料的均值和方差趨於常數，幾乎無波動(看上去比之前的陡峭，但是要注意他的值域只有[-0.05,0.05]之間)，所以直觀上可以認為是穩定的資料。另外DFtest的結果顯示，Statistic值原小於1%時的Critical value，所以在99%的置信度下，資料是穩定的。

4 時序資料的預測

在前面的分析可知，該序列具有明顯的年週期與長期成分。對於年週期成分我們使用視窗為12的移動平進行處理，對於長期趨勢成分我們採用1階差分來進行處理。

rol_mean = ts_log.rolling(window=12).mean()
rol_mean.dropna(inplace=True)
ts_diff_1 = rol_mean.diff(1)
ts_diff_1.dropna(inplace=True)
teststationarity(ts_diff_1)

結果如下

Test Statistic                  -2.709577
p-value                          0.072396
#Lags Used                      12.000000
Number of Observations Used    119.000000
Critical Value (1%)             -3.486535
Critical Value (5%)             -2.886151
Critical Value (10%)            -2.579896
dtype: float64

觀察其統計量發現該序列在置信水平為95%的區間下並不顯著，我們對其進行再次一階差分。再次差分後的序列其自相關具有快速衰減的特點，t統計量在99%的置信水平下是顯著的，這裡我不再做詳細說明。

ts_diff_2 = ts_diff_1.diff(1)
ts_diff_2.dropna(inplace=True)
teststationarity(ts_diff_2)

結果如下

Test Statistic                  -4.443325
p-value                          0.000249
#Lags Used                      12.000000
Number of Observations Used    118.000000
Critical Value (1%)             -3.487022
Critical Value (5%)             -2.886363
Critical Value (10%)            -2.580009
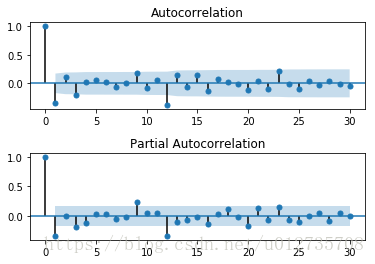
dtype: float64

資料平穩後，需要對模型定階，即確定p、q的階數。先畫出ACF,PACF的影象,程式碼如下：

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
def draw_acf_pacf(ts,lags):
    f = plt.figure(facecolor='white')
    ax1 = f.add_subplot(211)
    plot_acf(ts,ax=ax1,lags=lags)
    ax2 = f.add_subplot(212)
    plot_pacf(ts,ax=ax2,lags=lags)
    plt.subplots_adjust(hspace=0.5)
    plt.show()
draw_acf_pacf(ts_diff_2,30)

結果如下

觀察上圖，發現自相關和偏相係數都存在拖尾的特點，並且他們都具有明顯的一階相關性，所以我們設定p=1, q=1。下面就可以使用ARMA模型進行資料擬合了。（Ps.PACF是判定AR模型階數的，也就是p。ACF是判斷MA階數的，也就是q）

from statsmodels.tsa.arima_model import ARIMA
model = ARIMA(ts_diff_1, order=(1,1,1)) 
result_arima = model.fit( disp=-1, method='css')

模型擬合完後，我們就可以對其進行預測了。由於ARMA擬合的是經過相關預處理後的資料，故其預測值需要通過相關逆變換進行還原。

predict_ts = result_arima.predict()
# 一階差分還原
diff_shift_ts = ts_diff_1.shift(1)
diff_recover_1 = predict_ts.add(diff_shift_ts)
# 再次一階差分還原
rol_shift_ts = rol_mean.shift(1)
diff_recover = diff_recover_1.add(rol_shift_ts)
# 移動平均還原
rol_sum = ts_log.rolling(window=11).sum()
rol_recover = diff_recover*12 - rol_sum.shift(1)
# 對數還原
log_recover = np.exp(rol_recover)
log_recover.dropna(inplace=True)

我們使用均方根誤差（RMSE）來評估模型樣本內擬合的好壞。利用該準則進行判別時，需要剔除“非預測”資料的影響。

ts = ts[log_recover.index]  # 過濾沒有預測的記錄plt.figure(facecolor='white')
log_recover.plot(color='blue', label='Predict')
ts.plot(color='red', label='Original')
plt.legend(loc='best')
plt.title('RMSE: %.4f'% np.sqrt(sum((log_recover-ts)**2)/ts.size))
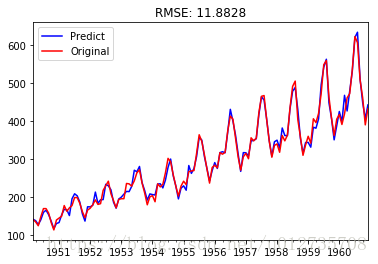
plt.show()

結果如下

看上面的結果，均方根誤差為11.8828，預測效果還是不錯的。

5 總結

ARIMA的建模過程如下：

• 獲取被觀測系統時間序列資料；
• 對資料繪圖，觀測是否為平穩時間序列；對於非平穩時間序列要先進行d階差分運算，化為平穩時間序列；
• 經過第二步處理，已經得到平穩時間序列。要對平穩時間序列分別求得其自相關係數ACF 和偏自相關係數PACF，通過對自相關圖和偏自相關圖的分析，得到最佳的階層 p 和階數 q
• 由以上得到的d、q、p，得到ARIMA模型。然後開始對得到的模型進行模型檢驗。

6 致謝