天池資料探勘比賽技術與套路總結
參加過兩次天池上的資料探勘比賽,成績不是很好,在此期間也看過不少比賽冠軍答辯ppt,檢視大量的資料。在此總結下,同時也分享給對資料探勘比賽有興趣的同學。希望下次比賽能取得個好的成績。
下面我將從下圖的流程開始講起。
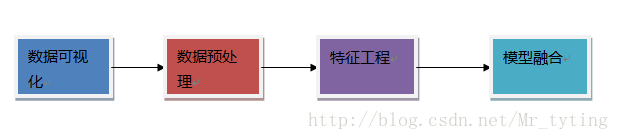
上面每一部分我都另外寫了博文專門講解,下面有連結。
資料視覺化
可以通過資料視覺化來驗證我們對資料分佈的一些猜想,使我們對資料分佈有一個清晰的認識和理解,並且由此設計一些合理的人工規則。
對資料進行視覺化可以清晰辨別資料樣本中是否有離群點,對後來的資料預處理有很大的幫助。
我的另外一篇部落格專門講如何對資料以及高維資料做視覺化處理。資料視覺化處理
資料預處理
一: 資料清洗
檢測異常樣本方法
根據對具體業務的理解和認識去除一些異常極端的資料。例如在對網頁瀏覽量的分析,可能需要去除爬蟲使用者的瀏覽資料。具體的處理方法請看我另外一篇博文的總結 機器學習–>檢測異常樣本方法總結
預設欄位的處理:分為四種情況
①預設值極多:如果缺值的樣本佔總數比例極高,我們可能就直接捨棄了,作為特徵加入的話,可能反倒帶入noise,影響最後的結果了。
②非連續特徵預設值適中:如果缺值的樣本適中,而該屬性非連續值特徵屬性(比如說類目屬性),那就把NaN作為一個新類別,加到類別特徵中
③連續特徵預設值適中:如果缺值的樣本適中,而該屬性為連續值特徵屬性,有時候我們會考慮給定一個step(比如age,我們可以考慮每隔2/3歲為一個步長),然後把它離散化,之後把NaN作為一個type加到屬性類目中。
④預設較少:考慮利用填充的辦法進行處理。這裡又有許多種填充的方法和技巧。以下我列出最常用的幾種辦法。
- 均值,眾數,中位數等填充辦法
>>> import numpy as np
>>> from sklearn.preprocessing import Imputer
>>> imp = Imputer(missing_values='NaN',strategy='mean', axis=0)
>>> imp.fit([[1, 2], [np.nan, 3], [7, 6]])
Imputer(axis=0, copy=True, missing_values='NaN' 需要注意的是:均值容易受到極端值的影響,不太穩定,故當用均值填充時,最好先剔除極端值,然後再算均值。或者用中位數填充,中位數受極端值影響較小。
- 模型填充辦法:比如用sklearn裡面的RandomForest模型去擬合數據樣本訓練模型,然後去填充缺失值
from sklearn.ensemble import RandomForestRegressor
### 使用 RandomForestClassifier 填補缺失的年齡屬性
def set_missing_ages(df):
# 把已有的數值型特徵取出來丟進Random Forest Regressor中
age_df = df[['Age','Fare', 'Parch', 'SibSp', 'Pclass']]
# 乘客分成已知年齡和未知年齡兩部分
known_age = age_df[age_df.Age.notnull()].as_matrix()
unknown_age = age_df[age_df.Age.isnull()].as_matrix()
# y即目標年齡
y = known_age[:, 0]
# X即特徵屬性值
X = known_age[:, 1:]
# fit到RandomForestRegressor之中
rfr = RandomForestRegressor(random_state=0, n_estimators=2000, n_jobs=-1)
rfr.fit(X, y)
# 用得到的模型進行未知年齡結果預測
predictedAges = rfr.predict(unknown_age[:, 1::])
# 用得到的預測結果填補原缺失資料
df.loc[ (df.Age.isnull()), 'Age' ] = predictedAges
return df, rfr
- 拉格朗日插值法
import pandas as pd
from scipy.interpolate import lagrange
inputfile = 'catering_sale.xls'
outputfile= 'sales.xls'
data = pd.read_excel(inputfile)#讀取excel
data[u'銷量'][(data[u'銷量']<400)|(data[u'銷量']>5000)]=None#異常值變為空值
def ployinterp_column(s,n,k=5):#預設是前後5個
#tem=list(range(n-k,n))+list(range(n+1,n+1+k))
y=s[list(range(n-k,n))+list(range(n+1,n+1+k))]#取數,n的前後5個,這裡有可能取到不存在的下標,為空
y=y[y.notnull()]#如果y裡面有空值的話就去掉
#teml=lagrange(y.index,list(y))#這裡代表的就是引數ai
return lagrange(y.index,list(y))(n)#最後的括號就是我們要插值的n
for i in data.columns:
if i==u'日期':
continue
for j in range(len(data)):
if(data[i].isnull())[j]:#空值進行插值
data[i][j] = ployinterp_column(data[i],j)
data.to_excel(outputfile)在保證原有資料樣本分佈不變情況下進行隨機填充
在[mean-std,mean+std]內隨機取數進行填充。
二: 資料取樣
在資料正負樣本不均衡情況下,當然正負樣本不要求1:1,但是也不能太大。這裡我們以正負樣本比例 1:10為例,把這樣不均衡的資料直接放進模型中進行訓練,準確率肯定很高,因為大部分都可以預測為負樣本。但是在測試集上效果很差。其泛化能力很弱。這時需要對資料進行取樣,使得資料樣本均衡。通常有四種辦法來進行取樣。
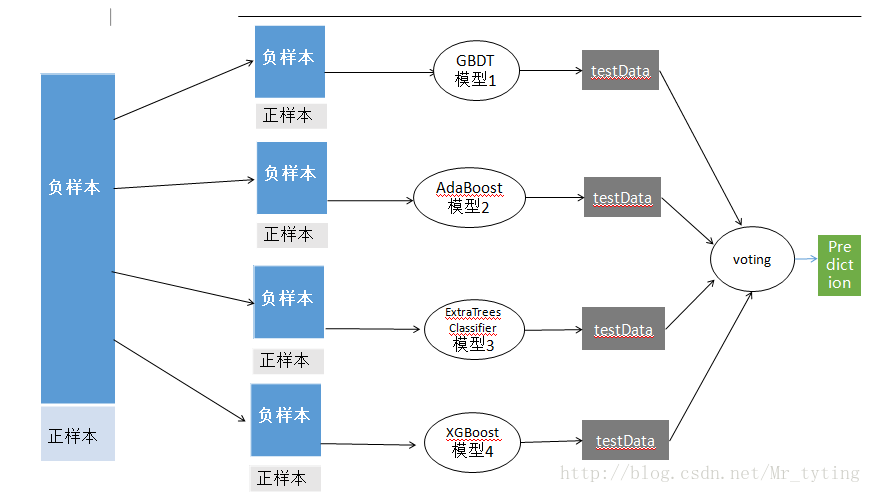
1. 從負樣本中抽取部分樣本出來和正樣本結合。(欠取樣,容易造成資訊損失)
將負樣本分為若干小份,即是對負樣本進行隨機的,有放回的取樣,將每一小份和正樣本結合成一個新的小的資料集,然後將這些若干個小的資料集放進不同分類器中進行訓練,然後在進行一個Bagging融合得出結果。
2 . 正樣本重複若干次(上取樣,保留的資料資訊但是有可能放大其噪聲資料)。
同上面道理一樣,對正樣本進行隨機的有放回的重複取樣使其數量上和負樣本比例均衡,這個過程進行多次,那麼就得出多個數據集。然後進行bagging。與欠取樣相比,效果往往略差。
3 . SMOTE(合成少數過取樣技術)

實現程式碼:
#encoding=gbk
from sklearn.neighbors import NearestNeighbors
import numpy as np
import random
class Smote:
#samples的最後一列是類標,都是1
def __init__(self, samples, N=10,k=5):
self.n_samples, self.n_attrs=samples.shape
self.N=N
self.k=k
self.samples=samples
def over_sampling(self):
if self.N<100:
old_n_samples=self.n_samples
print "old_n_samples", old_n_samples
self.n_samples=int(float(self.N)/100*old_n_samples)
print "n_samples", self.n_samples
keep=np.random.permutation(old_n_samples)[:self.n_samples]
print "keep", keep
new_samples=self.samples[keep]
print "new_samples", new_samples
self.samples=new_samples
print "self.samples", self.samples
self.N=100
N=int(self.N/100) #每個少數類樣本應該合成的新樣本個數
self.synthetic=np.zeros((self.n_samples*N, self.n_attrs))
self.new_index=0
neighbors=NearestNeighbors(n_neighbors=self.k).fit(self.samples)
print "neighbors", neighbors
for i in range(len(self.samples)):
nnarray=neighbors.kneighbors(self.samples[i],return_distance=False)[0]
#儲存k個近鄰的下標
self.__populate(N, i, nnarray )
return self.synthetic
#從k個鄰居中隨機選取N次,生成N個合成的樣本
def __populate(self, N, i, nnarray):
for i in range(N):
nn = np.random.randint(0, self.k)
dif=self.samples[nnarray[nn]]-self.samples[i] #包含類標
gap=np.random.rand(1,self.n_attrs)
self.synthetic[self.new_index]=self.samples[i]+gap.flatten()*dif
self.new_index+=1 4.代價敏感學習Cost Sensitive Learning
在lossFunction裡面給正樣本賦予較高權重,使得能夠更多的關注正樣本。
特徵工程
一:特徵處理
數值型:各種標準化,離散化(等頻,等寬離散化,長尾分佈直接二類化),歸一化,資料域變換(當你在原始資料上看不到資料內在的規律時,進行log,指數,Box-Cox變換可能會了解到資料的分佈情況),或者和其他特徵做一些組合特徵。
類別型:one-hot編碼
時間型:時間是否為一個節日,是否在一個時間段(類別型);或者計算距離某個日子變成間隔型;或者某個時間段內發生了多少次變成組合型等等;這個需要結合具體應用場景。使其變成離散型。
文字型:抽取特徵,n-gram;Bag of words;TF-IDF;word2vector等等。
統計型:根據具體應用場景,統計一些對結果有影響的資料,比如方差,均值等等。
組合特徵:對不同的特徵做個組合,比如我們利用基於樹的模型,挑選出最重要的一些特徵,我們對這些特徵兩兩做一些運算,比如加,減等運算,得到一些新的特徵集,在利用xgboost或者gbdt等對得到的新特徵集單獨訓練模型,並且得出新特徵集中特徵重要性排名,選取top k個特徵加入到原來的特徵集中。
上面處理的程式碼sklearn都有,可以檢視我的一篇博文和sklearn相關內容,上面有詳細的說明
資料預處理
sklearn特徵抽取
二:連續特徵離散化
離散化的重要性及其優勢:
離散特徵的增加和減少都很容易,易於模型的快速迭代;
稀疏向量內積乘法運算速度快,計算結果方便儲存,容易擴充套件;
離散化後的特徵對異常資料有很強的魯棒性:比如一個特徵是年齡>30是1,否則0。如果特徵沒有離散化,一個異常資料“年齡300歲”會給模型造成很大的干擾;
邏輯迴歸屬於廣義線性模型,表達能力受限;單變數離散化為N個後,每個變數有單獨的權重,相當於為模型引入了非線性,能夠提升模型表達能力,加大擬合;
離散化後可以進行特徵交叉,由M+N個變數變為M*N個變數,進一步引入非線性,提升表達能力;
特徵離散化後,模型會更穩定,比如如果對使用者年齡離散化,20-30作為一個區間,不會因為一個使用者年齡長了一歲就變成一個完全不同的人。當然處於區間相鄰處的樣本會剛好相反,所以怎麼劃分區間是門學問;
特徵離散化以後,起到了簡化了邏輯迴歸模型的作用,降低了模型過擬合的風險。
可以將缺失作為獨立的一類帶入模型。
將所有變數變換到相似的尺度上。
三:特徵選擇
特徵維度很高時,需要進行降維,可以檢視我的另一篇關於sklearn中特徵選擇的博文sklearn特徵選擇
過濾型(不常用)
sklearn.feature_selection.SelectKBest
包裹型
sklearn.feature_selection.RFE
嵌入型
feature_selection.SelectFromModel
Linear model,L1正則化
需要注意的是:如果在特徵選擇之前,最好不要用one-hot或者dummiesVriable對類別型進行編碼,因為特徵選擇時可能會剔除經one-hot衍生的一個特徵。
四:模型選擇
1 交叉驗證
1.1 K折交叉驗證:選擇不同的模型,檢視其在cross_validation上的好壞,取結果的平均值,增加結果的可信度。確定使用哪個模型。這部分可以檢視我的另一篇博文sklearn.cross_validation
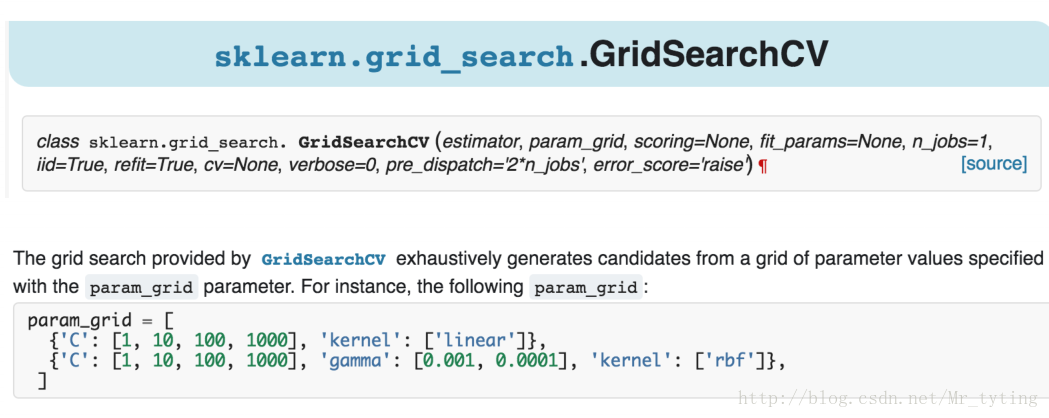
2 模型引數選擇
確定了某種模型,然後需要確定超引數。
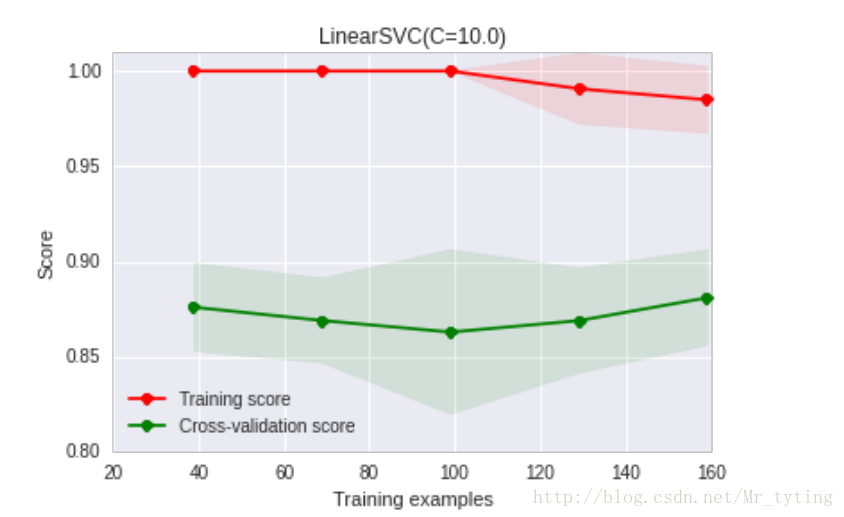
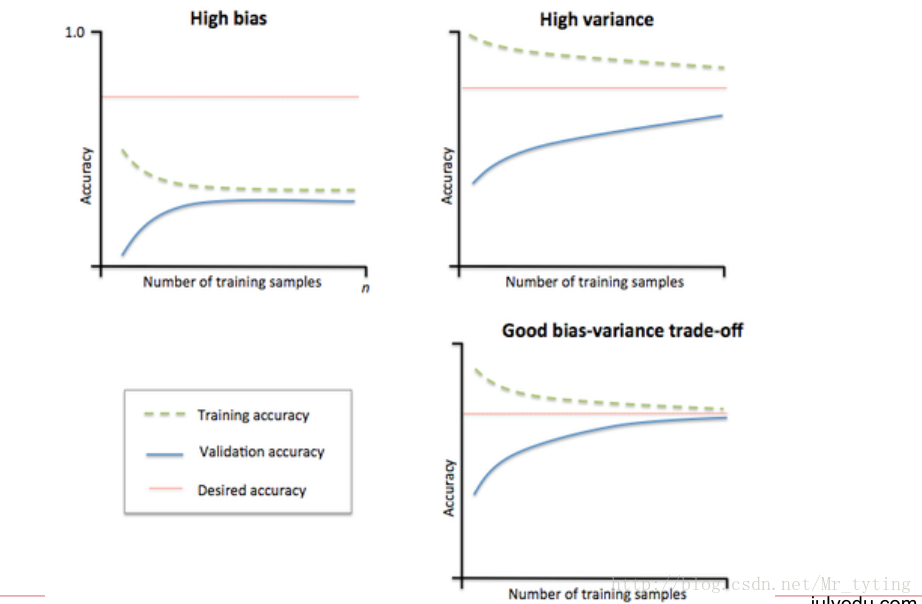
3 模型狀態評估
檢視當前引數的當前模型過擬合狀態還是欠擬合狀態。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.learning_curve import learning_curve
# 用sklearn的learning_curve得到training_score和cv_score,使用matplotlib畫出learning curve
def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None, n_jobs=1,
train_sizes=np.linspace(.05, 1., 20), verbose=0, plot=True):
"""
畫出data在某模型上的learning curve.
引數解釋
----------
estimator : 你用的分類器。
title : 表格的標題。
X : 輸入的feature,numpy型別
y : 輸入的target vector
ylim : tuple格式的(ymin, ymax), 設定影象中縱座標的最低點和最高點
cv : 做cross-validation的時候,資料分成的份數,其中一份作為cv集,其餘n-1份作為training(預設為3份)
n_jobs : 並行的的任務數(預設1)
"""
train_sizes, train_scores, test_scores = learning_curve(
estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes, verbose=verbose)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
if plot:
plt.figure()
plt.title(title)
if ylim is not None:
plt.ylim(*ylim)
plt.xlabel(u"訓練樣本數")
plt.ylabel(u"得分")
plt.gca().invert_yaxis()
plt.grid()
plt.fill_between(train_sizes, train_scores_mean - train_scores_std, train_scores_mean + train_scores_std,
alpha=0.1, color="b")
plt.fill_between(train_sizes, test_scores_mean - test_scores_std, test_scores_mean + test_scores_std,
alpha=0.1, color="r")
plt.plot(train_sizes, train_scores_mean, 'o-', color="b", label=u"訓練集上得分")
plt.plot(train_sizes, test_scores_mean, 'o-', color="r", label=u"交叉驗證集上得分")
plt.legend(loc="best")
plt.draw()
plt.gca().invert_yaxis()
plt.show()
midpoint = ((train_scores_mean[-1] + train_scores_std[-1]) + (test_scores_mean[-1] - test_scores_std[-1])) / 2
diff = (train_scores_mean[-1] + train_scores_std[-1]) - (test_scores_mean[-1] - test_scores_std[-1])
return midpoint, diff
plot_learning_curve(clf, u"學習曲線", X, y)
模型融合
1 Bagging(RandomForest)
1.1 用一個演算法
不用全部的資料集,每次取一個子集訓練一個模型
分類:用這些模型的結果做vote
迴歸:對這些模型的結果取平均
1.2 用不同的演算法
用這些模型的結果做vote 或 求平均
2 Stacking
用多種predictor結果作為特徵訓練