機器學習演算法——PCA演算法介紹以及Java實現
PCA演算法
一、演算法概述
主成分分析(PCA)是多元統計分析中用來分析資料的一種方法,PCA通過線性變換將原始資料變換為一組各維度線性無關的表示,可用於提取資料的主要特徵分量,常用於高維資料的降維。
PCA方法最著名的應用應該是在人臉識別中特徵提取及資料維,我們知道輸入200*200大小的人臉影象,單單提取它的灰度值作為原始特徵,則這個原始特徵將達到40000維,這給後面分類器的處理將帶來極大的難度。在這種情況下,我們必須對資料進行降維。
降維當然意味著資訊的丟失,不過鑑於實際資料本身常常存在的相關性,我們可以想辦法在降維的同時將資訊的損失儘量降低。
例如某淘寶店鋪的資料記錄為(日期, 瀏覽量, 訪客數, 下單數, 成交數, 成交金額),從經驗我們可以知道,“瀏覽量”和“訪客數”往往具有較強的相關關係,而“下單數”和“成交數”也具有較強的相關關係。這裡我們非正式的使用“相關關係”這個詞,可以直觀理解為“當某一天這個店鋪的瀏覽量較高(或較低)時,我們應該很大程度上認為這天的訪客數也較高(或較低)”。後面的章節中我們會給出相關性的嚴格數學定義。
這種情況表明,如果我們刪除瀏覽量或訪客數其中一個指標,我們應該期待並不會丟失太多資訊。因此我們可以刪除一個,以降低機器學習演算法的複雜度。所以,我們可以採用PCA進行降緯。
二、演算法原理
1、資料準備
假設有M個樣本,每個樣本有N個特徵,例如第i個(i=1,2,…,M)樣本為:
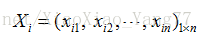
則M個樣本構成了M行N列的數值矩陣A。
2、資料歸一化處理
通常做法是將每一維的資料都減去該維的均值,使每一維的均值都為0。
3、計算協方差矩陣
協方差是一種用來度量兩個隨機變數關係的統計量,其定義為:
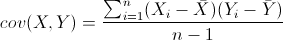
M*N樣本的協方差矩陣為:
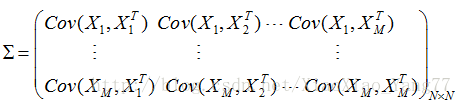
4、求出協方差矩陣的特徵值及對應的特徵向量
若AX=λX,則稱λ是A的特徵值,X是對應的特徵向量。實際上可以這樣理解:矩陣A作用在它的特徵向量X上,僅僅使得X的長度發生了變化,縮放比例就是相應的特徵值λ。
特別地,當A是對稱矩陣時,A的奇異值等於A的特徵值,存在正交矩陣Q(Q-1=QT),使得:

對A進行奇異值分解就能求出所有特徵值和Q矩陣。
A∗Q=Q∗DA∗Q=Q∗D,D是由特徵值組成的對角矩陣
由特徵值和特徵向量的定義知,Q的列向量就是A的特徵向量。
5、將特徵向量按對應的特徵值大小從上往下按行排列成矩陣,取前k行組成矩陣P,P為k行n列矩陣
6、Y=AP’ 即為降維到k維後的資料,Y為M行k列矩陣
三、程式碼實現
PCA.class
import java.util.ArrayList;
import java.util.Collections;
import java.util.HashMap;
import java.util.Iterator;
import 主函式呼叫PCA:
import Jama.Matrix;
import java.io.FileWriter;
import java.io.IOException;
public class PCAMain {
public static void main(String[] args) throws IOException {
// TODO Auto-generated catch block
SelectData selectData = new SelectData();
PCA pca = new PCA();
//獲得樣本集
double[][] primaryArray = selectData.getdatas();
System.out.println("--------------------------------------------");
double[][] averageArray = pca.changeAverageToZero(primaryArray);
System.out.println("--------------------------------------------");
System.out.println("均值0化後的資料: ");
System.out.println(averageArray.length + "行,"
+ averageArray[0].length + "列");
System.out.println("---------------------------------------------");
System.out.println("協方差矩陣: ");
double[][] varMatrix = pca.getVarianceMatrix(averageArray);
System.out.println("--------------------------------------------");
System.out.println("特徵值矩陣: ");
double[][] eigenvalueMatrix = pca.getEigenvalueMatrix(varMatrix);
System.out.println("--------------------------------------------");
System.out.println("特徵向量矩陣: ");
double[][] eigenVectorMatrix = pca.getEigenVectorMatrix(varMatrix);
System.out.println("--------------------------------------------");
Matrix principalMatrix = pca.getPrincipalComponent(primaryArray, eigenvalueMatrix, eigenVectorMatrix);
System.out.println("主成分矩陣: ");
// principalMatrix.print(6, 3);
System.out.println("--------------------------------------------");
System.out.println("降維後的矩陣: ");
Matrix resultMatrix = pca.getResult(primaryArray, principalMatrix);
// resultMatrix.print(6, 3);
int c = resultMatrix.getColumnDimension(); //列數
int r = resultMatrix.getRowDimension();//行數
System.out.println(resultMatrix.getRowDimension() + "," + resultMatrix.getColumnDimension());
}
}