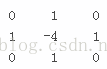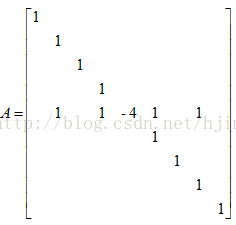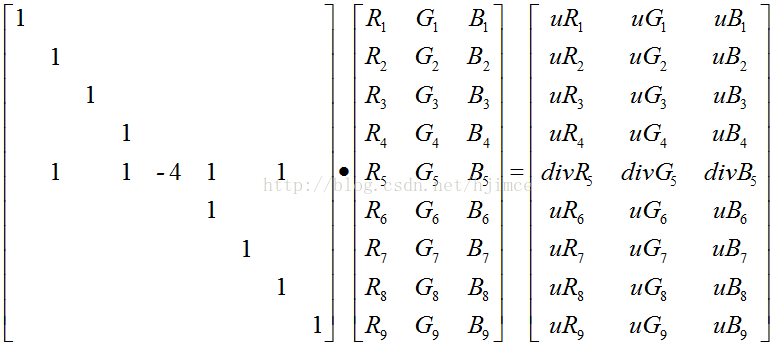影象處理(十二)影象融合(1)Seamless cloning泊松克隆-Siggraph 2004
Seamless cloning泊松克隆
作者:hjimce
本篇博文主要講解2004年Siggraph的經典paper:《Poisson Image Editing》,在影象融合領域,融合效果最牛逼的paper。講這個演算法,我沒打算講太多理論的公式,理論的東西,對於大部分數學比較差的人來說看了就頭暈。什麼散度、拉普拉斯運算元、梯度場、泊松方程、泊松方程第一類邊界條件(Dirichlet boundary)、泊松方程第二類邊界條件(Neumann boundary),如果把這些公式貼上來,估計很多人還沒看到演算法是怎麼實現的,就已經看不下去了。因此我將直接給出離散形式實現方法,演算法流程。
開始這個演算法前,我需要先講解一個數學問題:
一、散度計算
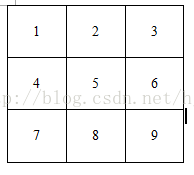
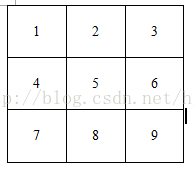
現在假設一幅影象為3*3的單通道灰度影象:
我們假設每一點的畫素值為V,V(1)表示畫素點1的值,那麼我們可以定義畫素點5的散度的計算公式為:
div(5)=[V(2)+V(4)+V(6)+V(8)]-4*V(5)
說白了就是通過拉普拉斯卷積核,進行卷積,就可以求解散度了。
拉普拉斯卷積核
當然正規的過程應該是先求解畫素點5的梯度值,然後在對梯度求導,這樣就能得到散度,不過得到的結果其實就是上面的計算公式。
二、泊松重建
OK,現在如果我給定一張影象,那麼是不是可以利用拉普拉卷積核,求解每個點的散度(這裡需要先說一下,後面用於泊松方程求解散度的時候,應該先求梯度,然後再對梯度求導得到散度,不要直接用卷積核,不然會犯我之前的一個錯誤,我之前就是直接用卷積核求解散度,導致邊界的地方出現了過渡不自然的現象)。
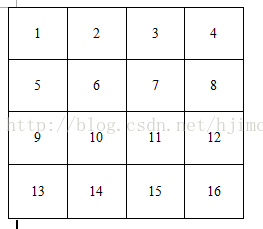
現在反過來,如果我給定每個畫素點的散度,我要你求解每個畫素點的值,要怎麼求取。這便是泊松方程的靈魂了。為了更好的理解重建過程,我現在假設影象的大小是4*4的16個畫素點圖片,如下:
ok,假設我給你畫素點6、7、10、11的散度值div(6)、div(7)、div(10)、div(11),那麼我們是不是可以列出如下4個方程:
[V(2)+V(5)+V(7)+V(10)]-4*V(6)=div(6)
[V(3)+V(6)+V(8)+V(11)]-4*V(7)=div(7)
[V(6)+V(9)+V(11)+V(14)]-4*V(10)=div(10)
[V(7)+V(10)+V(12)+V(15)]-4*V(11)=div(11)
這個時候,如果我們只有四個方程,可是裡面有16個畫素點,也就是說有16個未知數。因此單單靠上面的4個方程,就想把所有的畫素值求解出來是不可能的,這樣方程有無數多個解。因此我們需要新增約束方程,這個便是泊松重建方程的約束條件了。假設我們新增邊界約束條件,也就是說如果我已經知道了上面那副影象最外圍一圈的每個畫素點的值u,這樣我們就可以得到12個約束方程。即:
V(1)=u(1) V(2)=u(2) V(3)=u(3)
V(4)=u(4) V(5)=u(5) V(8)=u(8)
V(9)=u(9)
V(12)=u(12) V(13)=u(13)
V(14)=u(14) V(15)=u(15)V(16)=u(16)
上面有12個方程,外加給定的散度4個方程,這樣我們有16個方程。這樣就可以求解方程組了,這樣就能實現通過散度+邊界約束條件,實現影象重建。這個便是泊松方程的主要過程。
OK,不管影象多大,如果我們已經知道圖片最外一圈的畫素值(約束條件),以及其它畫素點的散度值,我們就能把這個方程給列出來,構建泊松方程,重建影象。如果到這裡你都看懂了,那麼我覺得其實已經可以開始寫影象融合的算了,是不是覺得演算法很簡單。說白了就是要求解一個方程組。
因此泊松融合,說的再簡單一點,就是構建方程組:
Ax=b
然後通過求解這個方程組得到每個畫素點的值。而演算法的整個過程可以說是怎麼構建方程組的b值 ,而係數矩陣其實是一個係數矩陣,矩陣的每一行有五個非零元素,對應於拉普拉斯演算法的卷積核。
三、泊松影象融合
泊松融合可以說是目前融合效果上等的演算法,泊松融合對應的文獻為《Poisson Image Editing》,這篇文獻叫基於泊松方程的影象編輯,沒有叫融合,是因為它的神奇功能不僅僅用於簡單的融合,還有一大堆的神器功能,當年我看到這篇文獻的時候,感覺相當神奇,這個演算法唯一的缺點是求解泊松方程需要一定的時間,速度比較慢。我之前自己看這paper把這篇文獻的程式碼寫過一遍,然而當時結果會出現偏色現象,所以一直以為自己沒有真正看懂這篇paper,而今重新回顧,才發現原來自己的思路沒有錯,就是一個引數搞錯了,計算散度的時候沒寫對。我們知道,對於一個畫素點的散度求解,其實就是拉普拉斯運算元濾波的結果:
拉普拉斯運算元
因為泊松重建,其實就是求解方程組:
Ax=b
演算法的整個過程在於求解係數稀疏矩陣A、及b。只要A、b求出來了,那麼我們就可以求解方程組得到x,而x就是我們得到的融合結果的畫素顏色值。
因此當時我想當然的以為,b的求解直接用拉普拉斯卷積核對源影象的興趣區域(ROI),進行卷積就可以得到散度b的值,因為對於給定的一幅影象散度其實就是通過拉普拉斯卷積核進行卷積,得到的結果,就是每個畫素點的散度。這種思路本沒有錯,然而這樣會出現邊界過渡不自然的現象。
而正確的思路應該是:求解ROI的梯度場Isrc,及背景影象不被修改的畫素區域的梯度場Idst。然後通過Isrc+Idst得到整幅待重建影象的梯度場,最後才根據梯度場求解散度。所以千萬不要偷懶,不要一步求解散度,要先把待重建影象的梯度場求好,再進行求解散度。
OK,再囉嗦一遍演算法的流程,看一下下面的圖片,
1、問題描述:
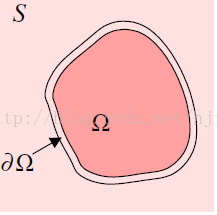
現在假設我們有影象g,,如下圖所示:
待克隆影象區域(ROI)
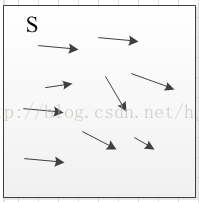
還有一張背景圖片S:
背景圖片S
現在我們希望把圖片g融合貼上到s中,且實現自然融合的效果:
2、演算法實現:
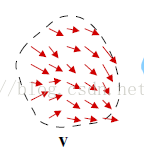
步驟1、計算影象g的梯度場。通過差分的方法,可以求得影象g的梯度場v:
ROI的梯度場
梯度場的求取知道怎麼求吧?如果連這都不會,那真的需要把影象最基本的東西好好看一看,說的簡單一點就是卷積,我們平時邊緣檢測的時候,就有用到過計算梯度的模長。在這裡我貼一下opencv的泊松融合這一步的程式碼:
computeGradientX(patch,patchGradientX);//計算ROI區域轉換複製到destination一樣大小的patch圖片x方向梯度
computeGradientY(patch,patchGradientY);//計算y方向梯度void Cloning::computeGradientX( const Mat &img, Mat &gx)
{
Mat kernel = Mat::zeros(1, 3, CV_8S);
kernel.at<char>(0,2) = 1;
kernel.at<char>(0,1) = -1;
if(img.channels() == 3)
{
filter2D(img, gx, CV_32F, kernel);
}
else if (img.channels() == 1)
{
Mat tmp[3];
for(int chan = 0 ; chan < 3 ; ++chan)
{
filter2D(img, tmp[chan], CV_32F, kernel);
}
merge(tmp, 3, gx);
}
}
void Cloning::computeGradientY( const Mat &img, Mat &gy)
{
Mat kernel = Mat::zeros(3, 1, CV_8S);
kernel.at<char>(2,0) = 1;
kernel.at<char>(1,0) = -1;
if(img.channels() == 3)
{
filter2D(img, gy, CV_32F, kernel);
}
else if (img.channels() == 1)
{
Mat tmp[3];
for(int chan = 0 ; chan < 3 ; ++chan)
{
filter2D(img, tmp[chan], CV_32F, kernel);
}
merge(tmp, 3, gy);
}
}這樣我們就可以計算出g的梯度場V(patchGradientX,patchGradientY)。
步驟2、計算背景圖片的梯度場:
computeGradientX(destination,destinationGradientX);//計算背景影象的x方向梯度
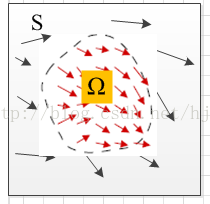
computeGradientY(destination,destinationGradientY);//計算背景影象y方向的梯度變數destination為背景影象。這樣就得到了背景圖片的梯度場(destinationGradientX,destinationGradientY),如下圖,下圖的梯度場我是隨便畫一畫的。
背景圖片的梯度場
步驟3、計算融合影象的梯度場。計算完了以後,我們就直接把ROI的梯度場覆蓋到S的梯度場上:
Mat laplacianX = Mat(destination.size(),CV_32FC3);
Mat laplacianY = Mat(destination.size(),CV_32FC3);
//因為前面已經對destinationGradientX做了固定區域的mask,patchGradientX做了修改區域的mask
laplacianX = destinationGradientX + patchGradientX;//求解整張圖片新的梯度場
laplacianY = destinationGradientY + patchGradientY;上面的程式碼需要注意的是destinationGradientX、destinationGradientY已經被做了mask操作,所以才能直接相加。具體的mask操作如下:
arrayProduct(destinationGradientX,binaryMaskFloatInverted, destinationGradientX);
arrayProduct(destinationGradientY,binaryMaskFloatInverted, destinationGradientY);//矩陣點乘,將lhs與rhs點乘得到result,因為有三個通道,估計mat不能實現三通道的矩陣的一次性點乘,所以才有這個函式
void Cloning::arrayProduct(const cv::Mat& lhs, const cv::Mat& rhs, cv::Mat& result) const
{
vector <Mat> lhs_channels;
vector <Mat> result_channels;
split(lhs,lhs_channels);//拆分成3個通道的矩陣
split(result,result_channels);
for(int chan = 0 ; chan < 3 ; ++chan)//三個矩陣進行分別相乘
multiply(lhs_channels[chan],rhs,result_channels[chan]);
merge(result_channels,result);//合成為一個
}上面函式中binaryMaskFloatInverted是一個mask,即Ω區域的值為0,非Ω區域的值為1。
待重建影象的梯度場
總之你只要把背景圖片的Ω區域的梯度場直接替換為g的梯度場v就可以了,因此如果你前面想簡化計算,其實背景圖片Ω區域的梯度場是不需要計算的,因為這一塊遲早會被g的梯度場替換掉,你只需要要計算背景圖片不被覆蓋的區域的梯度場就可以了。這一步就是得到待重建影象的梯度場。
步驟4、求解融合影象的散度。通過步驟3,我們可以得到每個畫素點的梯度值,也就是待重建影象的梯度場,因此接著我們需要對梯度求偏導,從而獲得散度。
computeLaplacianX(laplacianX,laplacianX);//求解梯度的散度 也就是拉普拉座標
computeLaplacianY(laplacianY,laplacianY);其相關呼叫函式:
void Cloning::computeLaplacianX( const Mat &img, Mat &laplacianX)
{
Mat kernel = Mat::zeros(1, 3, CV_8S);
kernel.at<char>(0,0) = -1;
kernel.at<char>(0,1) = 1;
filter2D(img, laplacianX, CV_32F, kernel);
}其實:
computeLaplacianX(laplacianX,laplacianX);//求解梯度的散度 也就是拉普拉座標
computeLaplacianY(laplacianY,laplacianY);lap = laplacianX + laplacianY;//散度步驟5、求解係數矩陣。OK,第4步我們已經把散度計算完畢,回顧一下前面的泊松重建方程,Ax=b,b便是散度,因此接著我們需要只要構建係數矩陣,還有約束方程就ok了,這一步因為opencv的原始碼是用了泊松方程的快速求解的方法,它沒有直接按我們的一般理解去求A,然後x=A-1*b。因為泊松方程有快速的求解方法,如果直接用求解A,然後求A得逆矩陣,那計算真不是一般的大。假如待重建影象的大小是1000*1000的,那麼係數矩陣的大小就是(1000*1000)X(1000*1000)的方陣。雖然A最後是稀疏矩陣,但是這麼龐大的矩陣,搞起來也要崩潰啊,其實也不是很慢,差不多也就幾十秒鐘的時間,計算機的計算速度感覺還是挺快的。這一步我貼一下其它的程式碼,因為opencv沒有直接構建A矩陣,它是用了泊松方程的快速求解演算法進行求解的,求解演算法裡面有正弦、餘弦函式,因此我猜它是用FFT方法求解泊松方程的,具體我沒有細看,也沒有必要細看,因為這個求解方程不該是我們關注的重點,我們需要關注的是怎麼構建這個方程。所以我還是得講一下普通的解法,係數矩陣A到底是個什麼玩意。
其實矩陣A,我前面已經提到過了。矩陣A的對角線的元素為-4,然後每行有對應的其它4個非零元素,其值為1,因為我們拉普拉斯卷積核的時候,就是這樣搞的。還有一點我們影象邊界畫素點的值應該為1。為了簡單理解,我現在回到博文最開始的部分:
 如果一幅影象,除了邊界畫素點之外,上面3*3影象的邊界畫素點為1、2、3、4、6、7、8、9。其它畫素點的散度(上圖中的畫素5)我都已經知道了。那麼我就可以列出泊松方程:
如果一幅影象,除了邊界畫素點之外,上面3*3影象的邊界畫素點為1、2、3、4、6、7、8、9。其它畫素點的散度(上圖中的畫素5)我都已經知道了。那麼我就可以列出泊松方程:
[V(2)+V(4)+V(6)+V(8)]-4*V(5)=div(5)
然後如果在把一幅影象的邊界畫素點的畫素值告訴你,那麼你就可以求解泊松方程了,假設約束點的值為u。以上面3*3的影象為例,最後係數矩陣A的構造為:
然後最後列出Ax=b的結果為:
這樣分別求解三個通道的方程,我們就可以獲得每個點的畫素R,G,B值了。再囉嗦一遍上面係數矩陣A的特點,影象最外圍一圈的邊界的對角線元素之為1,因為這些點是約束方程,其它的非邊界點就直接根據拉普拉斯的卷積核就可以了。到了這裡我覺得我應經講的沒法再詳細了,就這樣吧。opencv的原始碼如果你看不懂,建議看一下這個:http://eric-yuan.me/poisson-blending-2/
最後貼一下這個演算法的神器融合效果:
這篇博文只是講了《Poisson Image Editing》第一個功能,普通無縫融合功能。後面將繼續講解其它神器功能的實現,敬請期待。
作者:hjimce 聯絡qq:1393852684
最後把opencv的完整版普通融合的程式碼貼在這裡,供大家學習:
//無縫融合,這個函式其實沒什麼功能,只是為了減少、方便計算,先把要融合的區域裁剪下來,也就是對_src、_dst、_mask 進行裁剪到最小
//輸入:_src前景影象 _dst背景影象 _mask前景影象的mask,
//p是用於對應用的,p點指的是在dst中,待融合區域中心點(dst的待融合區域的大小是根據包含熊的矩形的大小確定的)
//輸出:_blend融合結果圖片
void cv::seamlessClone(InputArray _src, InputArray _dst, InputArray _mask, Point p, OutputArray _blend, int flags)
{
const Mat src = _src.getMat();
const Mat dest = _dst.getMat();
const Mat mask = _mask.getMat();
_blend.create(dest.size(), CV_8UC3);//融合後圖片的大小肯定跟背景影象一樣
Mat blend = _blend.getMat();
int minx = INT_MAX, miny = INT_MAX, maxx = INT_MIN, maxy = INT_MIN;
int h = mask.size().height;
int w = mask.size().width;
Mat gray = Mat(mask.size(),CV_8UC1);
Mat dst_mask = Mat::zeros(dest.size(),CV_8UC1);//背景影象的mask
Mat cs_mask = Mat::zeros(src.size(),CV_8UC3);
Mat cd_mask = Mat::zeros(dest.size(),CV_8UC3);
if(mask.channels() == 3)//如果給定的mask是彩色圖 需要轉換成單通道灰度圖
cvtColor(mask, gray, COLOR_BGR2GRAY );
else
gray = mask;
//計算包含mask的最小矩形,也就是把那隻熊包含起來的最小矩形框,這個矩形是位於src的,後面還有一個對應的矩形位於dst
for(int i=0;i<h;i++)
{
for(int j=0;j<w;j++)
{
if(gray.at<uchar>(i,j) == 255)
{
minx = std::min(minx,i);
maxx = std::max(maxx,i);
miny = std::min(miny,j);
maxy = std::max(maxy,j);
}
}
}
int lenx = maxx - minx;//計算矩形的寬
int leny = maxy - miny;//計算矩形的高
Mat patch = Mat::zeros(Size(leny, lenx), CV_8UC3);//根據上面的矩形區域,建立一個大小相同矩陣
int minxd = p.y - lenx/2;//計算dst的矩形
int maxxd = p.y + lenx/2;
int minyd = p.x - leny/2;
int maxyd = p.x + leny/2;
CV_Assert(minxd >= 0 && minyd >= 0 && maxxd <= dest.rows && maxyd <= dest.cols);
Rect roi_d(minyd,minxd,leny,lenx);//dst 興趣區域的矩形
Rect roi_s(miny,minx,leny,lenx);//src 興趣區域矩形
Mat destinationROI = dst_mask(roi_d);
Mat sourceROI = cs_mask(roi_s);
gray(roi_s).copyTo(destinationROI);//
src(roi_s).copyTo(sourceROI,gray(roi_s));
src(roi_s).copyTo(patch, gray(roi_s));//patch為
destinationROI = cd_mask(roi_d);
cs_mask(roi_s).copyTo(destinationROI);//cs_mask為把前景圖片的矩形區域影象 轉換到背景圖片矩形中的圖片
Cloning obj;
obj.normalClone(dest,cd_mask,dst_mask,blend,flags);
}//克隆融合外部介面函式
//輸入:destination背景圖片的整張圖片 binaryMask為destination待修改的畫素的mask
//patch是由src圖片的ROI區域複製過來的影象,其大小與destination相同,只有patch只有binaryMask區域存的是src的ROI圖片
//輸出:cloned融合結果整張圖片
void Cloning::normalClone(const Mat &destination, const Mat &patch, const Mat &binaryMask, Mat &cloned, int flag)
{
const int w = destination.cols;
const int h = destination.rows;
const int channel = destination.channels();
const int n_elem_in_line = w * channel;
//計算destination在x,y方向的梯度,獲得結果為:destinationGradientX destinationGradientY
//計算patch在x,y方向的梯度,獲得結果為: patchGradientX patchGradientY
//同時對binaryMask進行邊界腐蝕,去除毛刺,讓邊界變得光滑一點,同時把binaryMask歸一化為0~1得binaryMaskFloat
//其實這樣歸一化後binaryMaskFloat只有數值0,1 1代表即將被修改的畫素點
computeDerivatives(destination,patch,binaryMask);
//因為patch是一個src包含ROI的最小矩形塊圖片
//patchGradientX與binaryMaskFloat相乘,這樣patchGradientX就只剩下有用的區域了
arrayProduct(patchGradientX,binaryMaskFloat, patchGradientX);
arrayProduct(patchGradientY,binaryMaskFloat, patchGradientY);
evaluate(destination,binaryMask,cloned);
}void Cloning::computeGradientX( const Mat &img, Mat &gx)
{
Mat kernel = Mat::zeros(1, 3, CV_8S);
kernel.at<char>(0,2) = 1;
kernel.at<char>(0,1) = -1;
if(img.channels() == 3)
{
filter2D(img, gx, CV_32F, kernel);
}
else if (img.channels() == 1)
{
Mat tmp[3];
for(int chan = 0 ; chan < 3 ; ++chan)
{
filter2D(img, tmp[chan], CV_32F, kernel);
}
merge(tmp, 3, gx);
}
}
void Cloning::computeGradientY( const Mat &img, Mat &gy)
{
Mat kernel = Mat::zeros(3, 1, CV_8S);
kernel.at<char>(2,0) = 1;
kernel.at<char>(1,0) = -1;
if(img.channels() == 3)
{
filter2D(img, gy, CV_32F, kernel);
}
else if (img.channels() == 1)
{
Mat tmp[3];
for(int chan = 0 ; chan < 3 ; ++chan)
{
filter2D(img, tmp[chan], CV_32F, kernel);
}
merge(tmp, 3, gy);
}
}
void Cloning::computeLaplacianX( const Mat &img, Mat &laplacianX)
{
Mat kernel = Mat::zeros(1, 3, CV_8S);
kernel.at<char>(0,0) = -1;
kernel.at<char>(0,1) = 1;
filter2D(img, laplacianX, CV_32F, kernel);
}
void Cloning::computeLaplacianY( const Mat &img, Mat &laplacianY)
{
Mat kernel = Mat::zeros(3, 1, CV_8S);
kernel.at<char>(0,0) = -1;
kernel.at<char>(1,0) = 1;
filter2D(img, laplacianY, CV_32F, kernel);
}
void Cloning::dst(const Mat& src, Mat& dest, bool invert)
{
Mat temp = Mat::zeros(src.rows, 2 * src.cols + 2, CV_32F);
int flag = invert ? DFT_ROWS + DFT_SCALE + DFT_INVERSE: DFT_ROWS;
src.copyTo(temp(Rect(1,0, src.cols, src.rows)));
for(int j = 0 ; j < src.rows ; ++j)
{
float * tempLinePtr = temp.ptr<float>(j);
const float * srcLinePtr = src.ptr<float>(j);
for(int i = 0 ; i < src.cols ; ++i)
{
tempLinePtr[src.cols + 2 + i] = - srcLinePtr[src.cols - 1 - i];
}
}
Mat planes[] = {temp, Mat::zeros(temp.size(), CV_32F)};
Mat complex;
merge(planes, 2, complex);
dft(complex, complex, flag);
split(complex, planes);
temp = Mat::zeros(src.cols, 2 * src.rows + 2, CV_32F);
for(int j = 0 ; j < src.cols ; ++j)
{
float * tempLinePtr = temp.ptr<float>(j);
for(int i = 0 ; i < src.rows ; ++i)
{
float val = planes[1].ptr<float>(i)[j + 1];
tempLinePtr[i + 1] = val;
tempLinePtr[temp.cols - 1 - i] = - val;
}
}
Mat planes2[] = {temp, Mat::zeros(temp.size(), CV_32F)};
merge(planes2, 2, complex);
dft(complex, complex, flag);
split(complex, planes2);
temp = planes2[1].t();
dest = Mat::zeros(src.size(), CV_32F);
temp(Rect( 0, 1, src.cols, src.rows)).copyTo(dest);
}
void Cloning::idst(const Mat& src, Mat& dest)
{
dst(src, dest, true);
}
//輸入:img為背景影象、mod_diff為散度,mod_diff大小不包含img最外圍的畫素點
//也就是說矩陣mod_diff的大小為(w-2)*(h-2),並且mod_diff最外圍值(散度)為0
//輸出:result
//這個函式其實功能是快速求解泊松方程的一種方法,就是針對AX=B,由於泊松方程係數矩陣的特殊性
//這個方程的過程我們不需要深入理解
void Cloning::solve(const Mat &img, Mat& mod_diff, Mat &result)
{
const int w = img.cols;
const int h = img.rows;
//到了這裡其實mod_diff的寬為w-2 高為h-2
Mat res;
dst(mod_diff, res);//這個函式?
for(int j = 0 ; j < h-2; j++)
{
float * resLinePtr = res.ptr<float>(j);
for(int i = 0 ; i < w-2; i++)
{
resLinePtr[i] /= (filter_X[i] + filter_Y[j] - 4);
}
}
idst(res, mod_diff);
unsigned char * resLinePtr = result.ptr<unsigned char>(0);
const unsigned char * imgLinePtr = img.ptr<unsigned char>(0);
const float * interpLinePtr = NULL;
//first col
for(int i = 0 ; i < w ; ++i)
result.ptr<unsigned char>(0)[i] = img.ptr<unsigned char>(0)[i];
for(int j = 1 ; j < h-1 ; ++j)
{
resLinePtr = result.ptr<unsigned char>(j);
imgLinePtr = img.ptr<unsigned char>(j);
interpLinePtr = mod_diff.ptr<float>(j-1);
//first row
resLinePtr[0] = imgLinePtr[0];
for(int i = 1 ; i < w-1 ; ++i)
{
//saturate cast is not used here, because it behaves differently from the previous implementation
//most notable, saturate_cast rounds before truncating, here it's the opposite.
float value = interpLinePtr[i-1];
if(value < 0.)
resLinePtr[i] = 0;
else if (value > 255.0)
resLinePtr[i] = 255;
else
resLinePtr[i] = static_cast<unsigned char>(value);
}
//last row
resLinePtr[w-1] = imgLinePtr[w-1];
}
//last col
resLinePtr = result.ptr<unsigned char>(h-1);
imgLinePtr = img.ptr<unsigned char>(h-1);
for(int i = 0 ; i < w ; ++i)
resLinePtr[i] = imgLinePtr[i];
}
//泊松方程求解 輸入散度(laplacianX+laplacianY),及邊界點畫素即可重建求解
//輸入:img為背景圖片,laplacianX+laplacianY 為散度
//輸出:result重建結果
void Cloning::poissonSolver(const Mat &img, Mat &laplacianX , Mat &laplacianY, Mat &result)
{
const int w = img.cols;
const int h = img.rows;
Mat lap = Mat(img.size(),CV_32FC1);
lap = laplacianX + laplacianY;//散度
Mat bound = img.clone();
//邊界修正,opencv為了方便,直接把圖片最外圍的畫素點排除在外,不參與泊松重建
rectangle(bound, Point(1, 1), Point(img.cols-2, img.rows-2), Scalar::all(0), -1);
Mat boundary_points;
Laplacian(bound, boundary_points, CV_32F);
boundary_points = lap - boundary_points;
Mat mod_diff = boundary_points(Rect(1, 1, w-2, h-2));
solve(img,mod_diff,result);
}
void Cloning::initVariables(const Mat &destination, const Mat &binaryMask)
{
destinationGradientX = Mat(destination.size(),CV_32FC3);
destinationGradientY = Mat(destination.size(),CV_32FC3);
patchGradientX = Mat(destination.size(),CV_32FC3);
patchGradientY = Mat(destination.size(),CV_32FC3);
binaryMaskFloat = Mat(binaryMask.size(),CV_32FC1);
binaryMaskFloatInverted = Mat(binaryMask.size(),CV_32FC1);
//init of the filters used in the dst
const int w = destination.cols;
filter_X.resize(w - 2);
for(int i = 0 ; i < w-2 ; ++i)
filter_X[i] = 2.0f * std::cos(static_cast<float>(CV_PI) * (i + 1) / (w - 1));
const int h = destination.rows;
filter_Y.resize(h - 2);
for(int j = 0 ; j < h - 2 ; ++j)
filter_Y[j] = 2.0f * std::cos(static_cast<float>(CV_PI) * (j + 1) / (h - 1));
}
//binaryMask為影象destination待修改的區域的mask
void Cloning::computeDerivatives(const Mat& destination, const Mat &patch, const Mat &binaryMask)
{
initVariables(destination,binaryMask);//相關變數初始化,沒用的東西
computeGradientX(destination,destinationGradientX);//計算背景影象的x方向梯度
computeGradientY(destination,destinationGradientY);//計算背景影象y方向的梯度
computeGradientX(patch,patchGradientX);//計算ROI區域轉換複製到destination一樣大小的patch圖片x方向梯度
computeGradientY(patch,patchGradientY);//計算y方向梯度
Mat Kernel(Size(3, 3), CV_8UC1);
Kernel.setTo(Scalar(1));
erode(binaryMask, binaryMask, Kernel, Point(-1,-1), 3);//對binaryMask進行腐蝕,去掉邊界的毛刺點,讓邊界曲線平滑一點
binaryMask.convertTo(binaryMaskFloat,CV_32FC1,1.0/255.0);
}
void Cloning::scalarProduct(Mat mat, float r, float g, float b)
{
vector <Mat> channels;
split(mat,channels);
multiply(channels[2],r,channels[2]);
multiply(channels[1],g,channels[1]);
multiply(channels[0],b,channels[0]);
merge(channels,mat);
}
//矩陣點乘,將lhs與rhs點乘得到result,因為有三個通道,估計mat不能實現三通道的矩陣的一次性點乘,所以才有這個函式
void Cloning::arrayProduct(const cv::Mat& lhs, const cv::Mat& rhs, cv::Mat& result) const
{
vector <Mat> lhs_channels;
vector <Mat> result_channels;
split(lhs,lhs_channels);//拆分成3個通道的矩陣
split(result,result_channels);
for(int chan = 0 ; chan < 3 ; ++chan)//三個矩陣進行分別相乘
multiply(lhs_channels[chan],rhs,result_channels[chan]);
merge(result_channels,result);//合成為一個
}
//泊松重建
void Cloning::poisson(const Mat &destination)
{
Mat laplacianX = Mat(destination.size(),CV_32FC3);
Mat laplacianY = Mat(destination.size(),CV_32FC3);
//因為前面已經對destinationGradientX做了固定區域的mask,patchGradientX做了修改區域的mask
laplacianX = destinationGradientX + patchGradientX;//求解整張圖片新的梯度場
laplacianY = destinationGradientY + patchGradientY;
computeLaplacianX(laplacianX,laplacianX);//求解梯度的散度 也就是拉普拉座標
computeLaplacianY(laplacianY,laplacianY);
split(laplacianX,rgbx_channel);//通道拆分
split(laplacianY,rgby_channel);
split(destination,output);
for(int chan = 0 ; chan < 3 ; ++chan)
{
poissonSolver(output[chan], rgbx_channel[chan], rgby_channel[chan], output[chan]);
}
}
//輸入:I背景整張圖片 wmask背景中待修改的區域的mask
//輸出:cloned
void Cloning::evaluate(const Mat &I, const Mat &wmask, const Mat &cloned)
{
bitwise_not(wmask,wmask);//矩陣元素取反操作,這樣背景圖片保持不變的畫素對應的mask值為1
wmask.convertTo(binaryMaskFloatInverted,CV_32FC1,1.0/255.0);
//上面已經對patchGradientX做了mask操作 ,這邊也對destinationGradientX做mask操作
arrayProduct(destinationGradientX,binaryMaskFloatInverted, destinationGradientX);
arrayProduct(destinationGradientY,binaryMaskFloatInverted, destinationGradientY);
poisson(I);
merge(output,cloned);
}上面的程式碼對應於opencv的這個演算法的第一個功能“Normal Cloning”,後面還有五大神奇的功能。其具體功能選項如下:
具體使用看文獻《Poisson Image Editing》
* 1- Normal Cloning
* 2- Mixed Cloning 1與2的區別見文獻圖片6
* 3- Monochrome Transfer 細節風格轉換文獻中的圖片5,這個就像paper《Style Transfer for Headshot Portraits》一樣的功能
* 4- Color Change 文獻圖片11
* 5- Illumination change 文獻圖片10
* 6- Texture Flattening 文獻圖片9
參考文獻:
1、Opencv3.0
2、《Poisson Image Editing》