實際上類似的曲線可以做很多，參考Benice的部落格（或者此處上一篇部落格轉發的少量圖片），但是這個五角星形狀的曲線比較簡單。

我從來只是把網路上BBS或部落格之類的寫的東西當作一種消遣而不是研究，所以，不能指望對文字內容從語法上嚴格推敲，除非很有興趣也不太可能過問對我來說太艱澀繁複又非自己必須做的事情。——除非有合法而可觀的佣金

圓圓相切的情況下謀點運動軌跡的描述，通過調整引數可以作出各種曲線，如果仔細研究，比如benice那樣詳細的總結，專門發一篇華麗麗的中文核心論文也沒太大問題，但是我對發這種論文不感興趣。

我只說說自己是怎麼用Geogebra繪製出下面這條五角星形曲線的；為了網路上交流方便，這也是動機之一，還作成GIF動畫的形式。

實際上在知道曲線引數方程之前是需要嘗試的，這就是為什麼說Matlab雖然強大，遠不如geogebra方便的原因。術業有專攻。

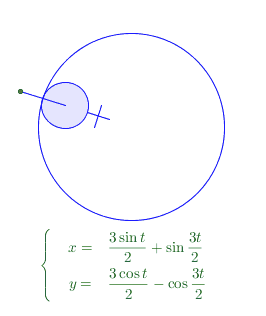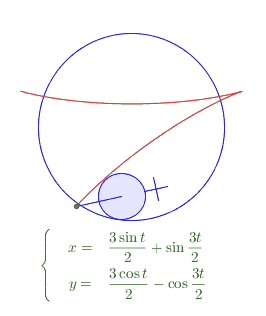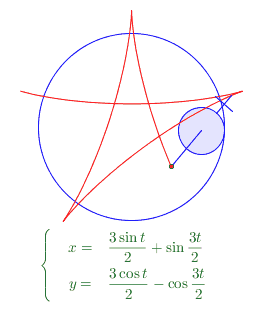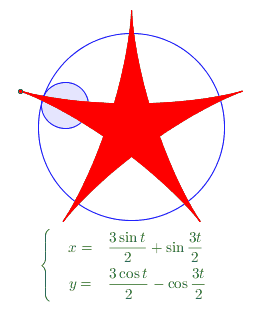
得到這樣的五角星曲線純屬偶然，我先繪製一個以O=(0,0)為圓心半徑為2的藍色圓；然後以A=(1.5,0)為圓心繪製一個半徑0.5的圓。這就是兩個將要發生摩擦的圓。這個時候，我還不知道自己能畫出什麼曲線。考慮到小圓的圓心是運動的，所以，實際上(1.5,0)只是初始狀態的值，我建立了一個geogebra中以角度為單位的slider變數，比如叫他alpha,或t,然它初值為0， A=1.5*(cos[t],sin[t]) 才是A的真實的座標引數。

最初想要表達一個圓的滾動，我是用給圓增加一系列輻條的方式來實現，但是對照之下，發現benice的給圓增加一個“把”的方式視覺效果要好得多。所以就欣然借鑑了。

這個繪製是很簡單的。增加這樣的一個“把”是簡單的操作。關鍵在於，這個把看上去似乎是總跟OA共線的，實際上運動起來發現，如果它總是跟OA共線，則運動軌跡總是圓！！ 所以，這個“把”在A點運動（或slider的值變化）的同時，相對於當前t時刻的OA還在發生旋轉。 ——也就是小圓A在大圓O內側滾動的同時，還在自旋，有相對滑動。我假設這個滑動的角速度是 n*t (n為有理數）。 結果發現，n=5/2的時候得到的就是上圖的五角星形狀的曲線。

下面是製作的ggb檔案的截圖，希望對同樣使用Geogebra的初學者有幫助：

這個時候已經知道的五角星形狀的曲線是怎麼來的了，但Geogebra還不能太容易得到它的最簡單的引數方程，好了，把這項光榮而艱鉅的任務交給Mathematica好了（選好工具選對人）

於是引數方程很容易就求出來了。如圖所示。

很容易發現第二項的係數決定著五角星的"肥瘦程度"

Manipulate[
 ParametricPlot[{3 Sin[t]/2 + a Sin[3 t/2], 
   3 Cos[t]/2 - a Cos[3 t/2]}, {t, 0, 4 Pi}, PlotStyle -> Red, 
  Axes -> False], {a, 1/2, 1}]

它要變成一朵花也沒辦法:

Manipulate[
 ParametricPlot[{ Sin[t] + a Sin[3 t/2], Cos[t] - a Cos[3 t/2]}, {t,    0, 4 Pi}, PlotStyle -> Red, Axes -> False], {a, 1/3, 1}]