深度強化學習:入門(Deep Reinforcement Learning: Scratching the surface)
本部落格是對學習李巨集毅教授在youtube上傳的課程視訊《Deep Reinforcement Learning: Scratching the surface》所做的筆記,供大家學習參考。
熱度起源
- 15年2月:Google在nature上的文章,用RL玩atari遊戲,可以超越人類玩家表現。
- 16年春天:基於RL的Alphago橫掃人類棋手。
RL的方案
兩個主要物件:Agent和Environment
Agent觀察Environment,做出Action,這個Action會對Environment造成一定影響和改變,繼而Agent會從新的環境中獲得Reward。迴圈上述步驟。
舉例:
機器人把水杯打翻了,人類說“不能這麼做”,機器人獲得人類的這個負向反饋,然後機器人觀察到水杯打翻的狀態,採取了拖地的行為,獲得了人類的“謝謝”的正向反饋。
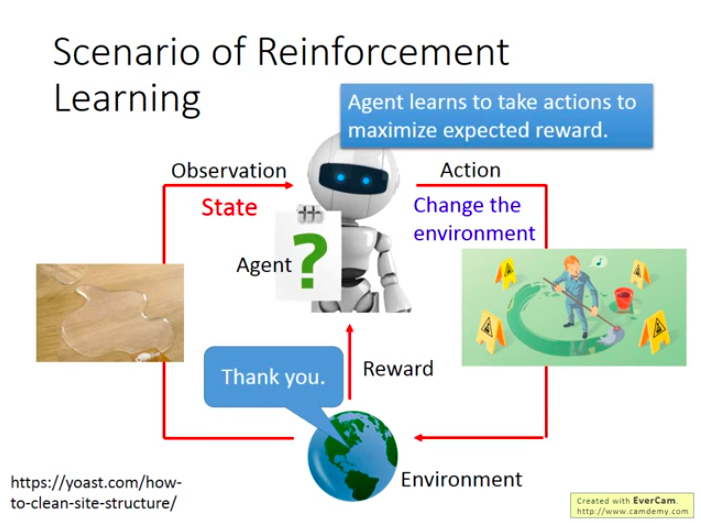
Agent學習的目標就是使得期望的回報(reward)最大化。
注意:State(observation說法更貼切)指的是Agent觀察到的Environment的狀態,不是指machine本身的狀態。
以Alphago為例子:
對Alphago來說,Observation就是19×19的一個棋盤,於是它落下一黑子:
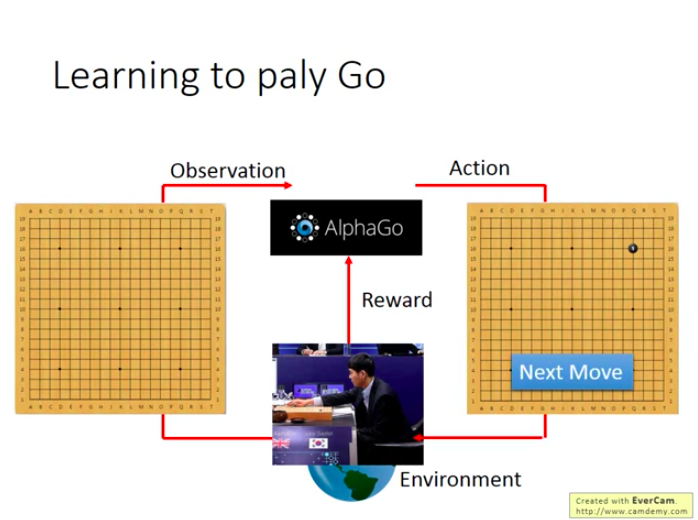
然後對手下了一個白子,Alphago觀察到一個新Observation(有兩顆棋子的),再下一顆黑子:

不過RL比較困難的一個地方是:Reward是比較難獲得的,而Agent就是依靠Reward來進行學習,進行自身策略的調整。
學習Go:監督學習與增強學習
- 監督學習的行動方案(跟著老師學):
看到一個局式,機器就從經驗中找尋和這個局式相同的那個做法,並採取經驗中的應對方法,因為通過經驗瞭解到這種應對方法是最好的(只是經驗中的最好,並不代表對於Go的局勢來說真的最好)。然而問題也就在於,人類也不知道哪一種應對方法時最優的,所以讓機器從人類棋譜中學習,可能可以下的不錯,但不一定是最厲害的。
- RL的行動方案(從經驗中學習)
機器自己去和別人下圍棋,贏了就是正反饋,輸了就是負反饋。不過機器不知道自己下的那麼多步裡面哪些好,哪些不好,需要自己去搞清楚。
不管是哪種方法,都需要有大量的訓練例子,比如監督學習要看上千萬的棋譜,RL要下上千萬盤的棋。不過對於RL來說,很難有人類和它下幾千萬盤棋,所以策略是先用監督學習訓練處兩個下得還可以的機器,再讓它們用RL互相對著下。

RL也可以用在聊天機器人的訓練上:
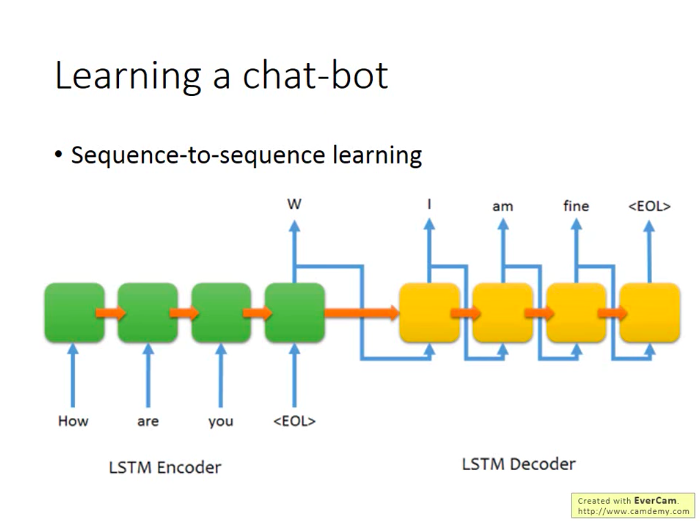
同樣有監督學習和RL的學習差別:
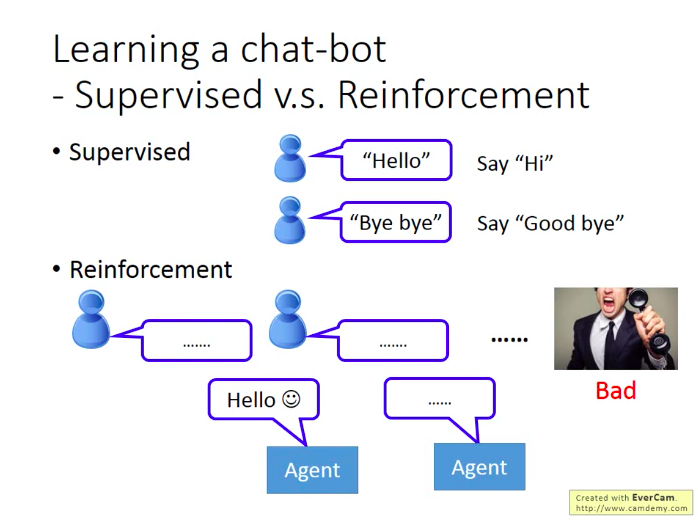
- 監督學習
如果對方說”hello”,機器應該回復”Hi”;如果對方說”Bye bye”,機器應該回復”Good bye”。
- 增強學習
機器和對方瞎說,最後獲得人類怒掛電話的負反饋(滑稽)。但機器仍不知道是自己哪句話沒講對,要靠自己去弄清楚。
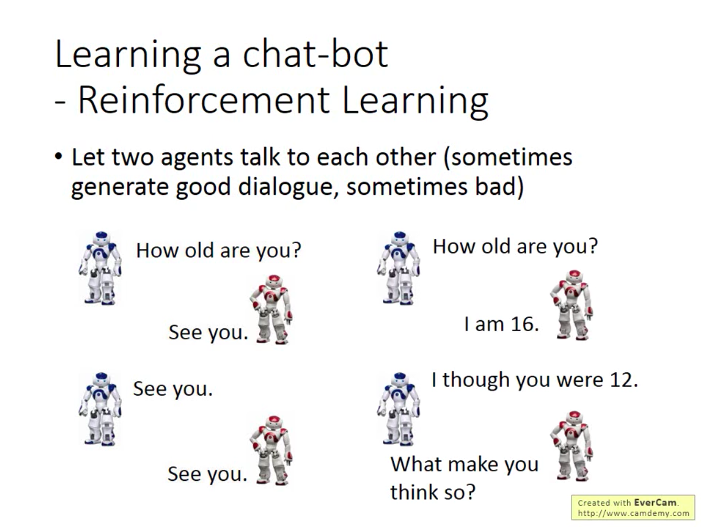
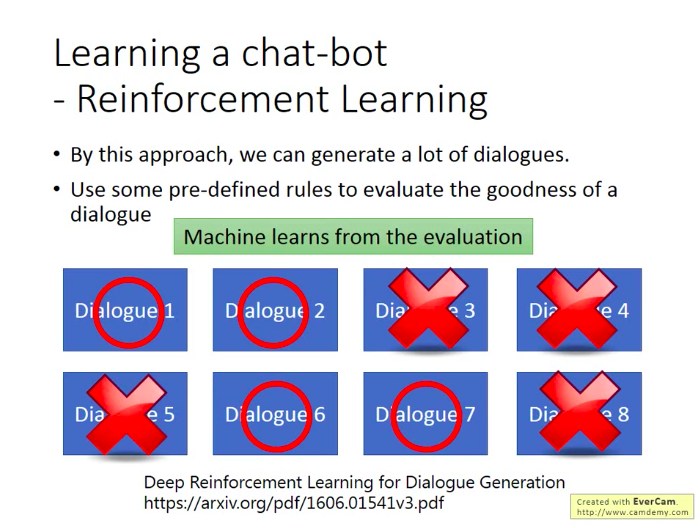
同樣,由於需要大量訓練,現實的訓練方法是先用監督學習訓練兩個機器人,再讓兩個機器人通過RL互相講話。不過還是需要有人來判斷機器的對話是好還是不好,這是用程式很難判斷的。(目前尚需克服的一個問題,有文獻嘗試給出一些簡單規則來判斷好不好,好就給機器人正反饋,不好就給負反饋)。
同樣,很可能接下來會有人用GAN來做訓練,即訓練一個discriminator,去學習人類之間和機器之間的對話,然後判斷一段新對話是來自人類,還是機器。而Agent的對話會盡量”騙過“discriminator,想辦法生成儘可能像人類的對話。
更多應用
互動式檢索:
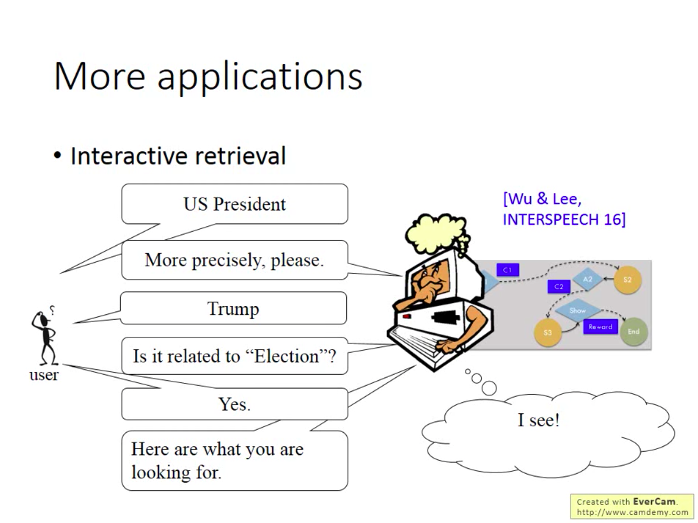
開直升機、無人駕駛、智慧節電、文字生成:

玩電腦遊戲:
機器用RL學習玩遊戲和人類是一樣的輸入:電腦螢幕(畫素輸入),而不是像傳統的遊戲內建AI,是通過從程式裡面直接獲得某些資料來進行行動。RL的機器通過自主學習以採取合適的行為。

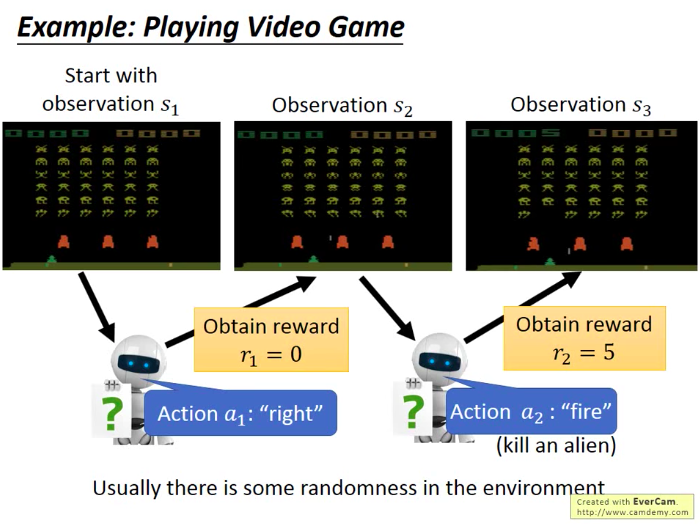
比如經典的太空入侵者遊戲:飛機有三種行動選擇,開火,左移,右移。Reward是遊戲介面上的分數(不是看畫素)。
如下圖,飛機觀察到第一種情況s1,決定右移,結果返現反饋為0,這時它觀察完當前情況s2,選擇開火,殺死一個外星人,發現獲得了5的reward。觀察到新的情況s3(少了一個外星人),繼續行動…… 遊戲從一次開始到結束稱為一個episode,而機器的學習目標就是最大化每個episode的累積分數。

RL的難點
- Reward Delay
- Agent’s actions affect the subsequent data it receives

後面內容的大綱
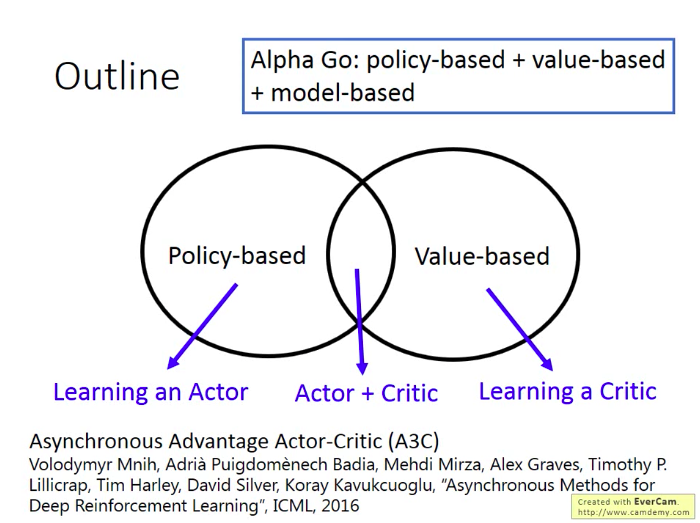
RL的方法分成兩部分:
- Policy-based:學習到一個Actor
- Value-based:學習到一個Critic
將Actor與Critic結合起來是目前最有效果的做法。

Policy-based Approach: Learning an Actor
機器學習的本質就是找一個“函式”,而RL是機器學習的一種,而RL要找到的這個函式就是Actor/Policy=
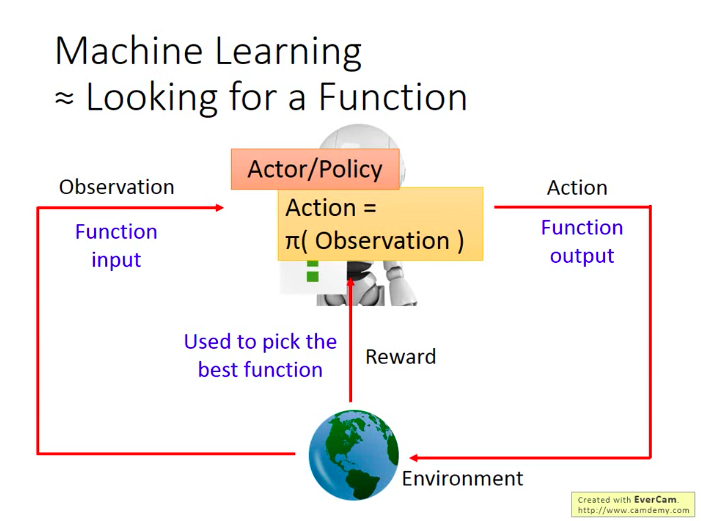
而找到這個函式有三個步驟,如下圖(當我們的Actor是一個Neural Network構成的時候,我們做的就是Deep Reinforcement Learning):
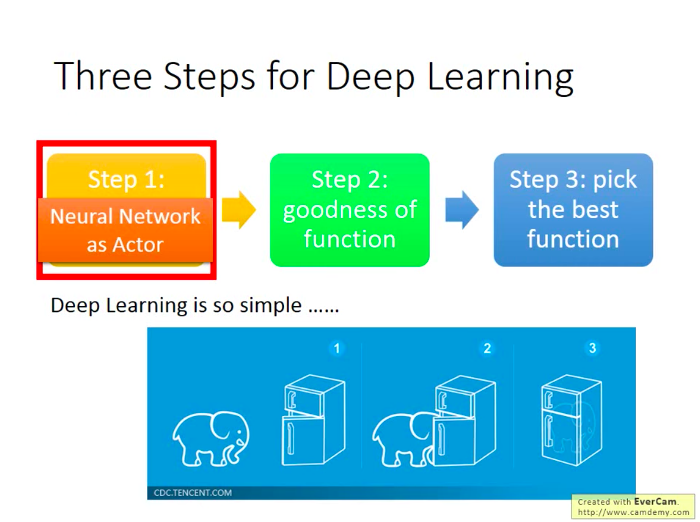
- 第一步:確定函式集合(選擇一個充當Actor的模型)
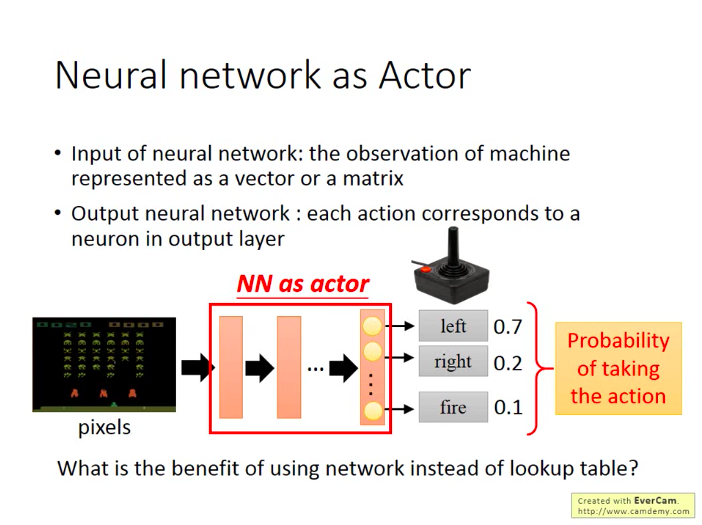
假設還是在之前的遊戲裡面,那麼作為Actor的輸入就是遊戲畫面,因此我們作為Actor的NN一定不是簡答的前饋神經網路,應該還會有一些卷積層。而Actor的輸出就是玩家可以進行的操作(action):左移,右移,開火。即作為Actor的NN的書輸出層只要三個神經元即可,每個神經元代表一種玩家操作的選擇,而神經元的輸出是對於該操作所對應的分數。而我們就可以選擇分數最高的action。
不過如果是在做policy-based的時候,我們通常假設Actor是隨機的(stochastic),即Actor的輸出是各個操作對應的概率值,而不是得分。後面的lecture裡面也假設Actor都是隨機的。
- NN相對搜尋表(lookup table)的優點
搜尋表的做法是:窮舉每種遊戲狀況的可能,並給出對應狀況下的最優操作。所以可以得到搜尋表,就只需要一一對應地去找對應狀況地給出的最優操作去執行就可以了。
不過在Actor玩電腦遊戲的時候,搜尋表的做法就不可行了,因為我們的輸入時遊戲畫面(畫素),不太可能窮盡所有畫素的組合情況,所以只能用神經網路來替代搜尋表的做法。而且NN是有舉一反三的能力的,即就算有些情況它之前沒見過,它也可能給出一個比較合理的結果。
- 第二步:確定函式的效能
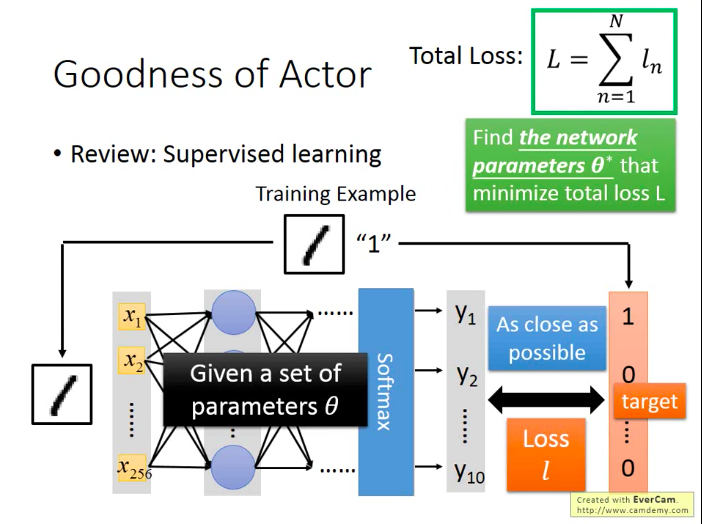
在監督學習裡面,我們的做法通常是:給定訓練樣本,然後訓練得到模型的引數,再講測試樣本輸入到訓練好的模型中,看模型的輸出結果與真實值“像”不“像”,越“像”就說明模型(函式)訓練得越好。而為了獲得最好的模型,我們定義了一個衡量模型輸出與真實值之間“差距”的變數叫損失函式(Loss),所有訓練樣本的損失加總就得到了成本函式/總損失,我們就會去嘗試尋找能夠讓總損失總小的模型引數,而這個模型引數找到後,也就確定了最優的模型/函式。
在RL中,對於函式的“好壞”的定義其實與監督學習中的也是非常相似的:比如我們直接讓訓練過的Actor去玩遊戲,並獲得一輪遊戲(episode)結束最後的總Reward(
不過有個問題是:就算我們用相同的Actor去玩同一款遊戲,也可能獲得不同的Reward,兩個原因:
- Actor本身是隨機的,相同情況下(Observation)可能採取不同的操作(Action)。
- 遊戲本身有隨機性。即使Actor採取相同的操作(Action),遊戲可能給出不同的反饋(Observation)。
因此,我們應該最大化的目標值不是某一輪遊戲的Reward,而是Reward的期望值

那麼
首先,我們將一輪遊戲(episode)視作一個過程(trajectory):
而總Reward為:
每個
那麼總回報的期望值就為:
不過,因為
因此,我們計算總回報期望值的公式也可以寫成:
這樣,期望總回報就具備可計算性了。

- 第三步:選擇最優的函式

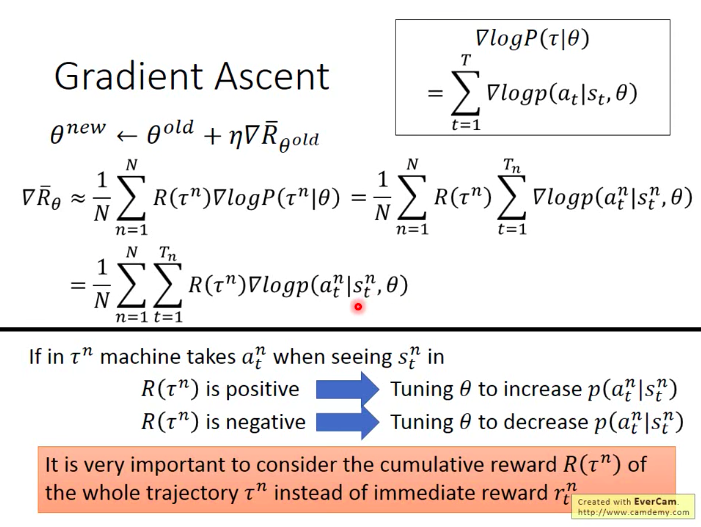
那麼,接下來,我們就用梯度上升(Gradient Ascent)的方法去找到可以最大化

具體如何計算期望總回報的梯度呢?
因為
接下來,針對

最後,我們的計算難點落腳在計算

然後取log,相乘變相加,並且和

最後,我們得到總期望回報的梯度可以表示成如下形式: