有一種樹叫做線段樹,有一種陣列叫做樹狀陣列
近日受到微軟程式設計之美大賽第二題和hdu一些題目變態般的大資料的刺激,而且老是聽到群裡的一些大神講什麼線段樹,樹狀陣列,分桶法呀等等一系列不明覺厲的東西,花了幾天好好看了下線段樹和樹狀陣列,下面我來分享一些,我的心得和感悟,如有不足之處歡迎大神們前來狂噴。
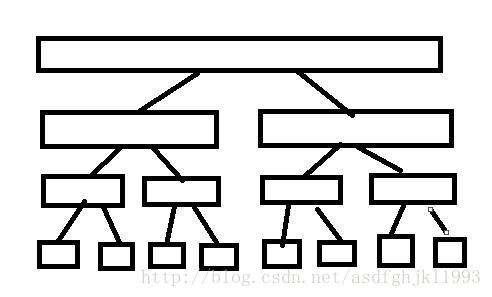
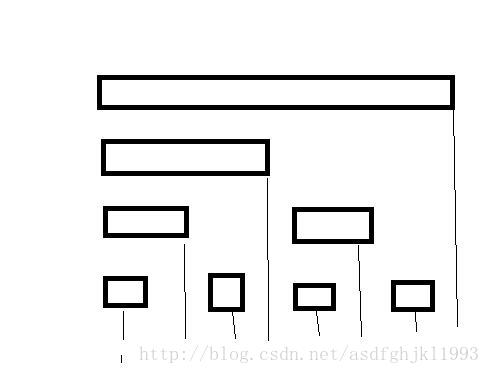
線段樹和樹狀陣列都是一種擅長處理區間的資料結構。它們間最大的區別之一就是線段樹是一顆完美二叉樹,而樹狀陣列(BIT)相當於是線段樹中每個節點的右兒子去掉。
如圖:
線段樹
樹狀陣列:
樹狀陣列一般適用於三類問題:
1,修改一個點求一個區間
2,修改一個區間求一個點
3,求逆序列對
而用樹狀陣列能夠解決的問題,用線段樹肯定能夠解決,反之則不一定。但是樹狀陣列有一個明顯的好處就是較為節省空間,實現要比線段樹要容易得多,而且在處理某些問題的時候使用樹狀陣列效率反而會高得多。 昨天看到某位大牛在部落格上也留下了這樣一句話,線段樹擅長處理橫向區間的問題,樹狀陣列擅長處理縱向區間的問題,可能由於水平有限,暫時還木有體會到這一點。。。。憂傷。。。
下面我們來看兩道比較基礎的線段樹模板題
首先是點修改的:
一次修改一個點,然後查詢最大值還有和:
void update(int u,int v,int o,int l,int r) { int m=(l+r)/2; if(l==r) { maxv[o]=v; sum[o]=v; } else { if(u<=m) update(u,v,o*2,l,m); else update(u,v,o*2+1,m+1,r); maxv[o]=max(maxv[o*2],maxv[o*2+1]); sum[o]=sum[o*2]+sum[o*2+1]; } } int query_sum(int ql,int qr,int o,int l,int r) { int m=(l+r)/2; if(ql<=l&&r<=qr) return sum[o]; if(ql<=m) return query_sum(ql,qr,o*2,l,m); if(m<qr) return query_sum(ql,qr,o*2+1,m+1,r); } int query_max(int ql,int qr,int o,int l,int r) { int m=(l+r)/2,ans=-1; if(ql<=l&&r<=qr) return maxv[o]; if(ql<=m) return max(ans,query_max(ql,qr,o*2,l,m)); if(m<qr) return max(ans,query_max(ql,qr,o*2+1,m+1,r)); }
然後是區間修改的:
Uva11992這道題是劉汝佳厚白書中的例題
大意為對一個矩陣進行操作,選擇其中子矩陣(x1,y1,x2,y2)可以讓它每個元素增加v
也可以讓它每個元素等於v,也可以查詢這個子矩陣的元素和,最小值,最大值。
解決方法當然是線段樹,不過對於這棵線段樹的update,對於set操作要請除節點上的
Addv標記,但對於add操作不清楚setv標記,在maintain函式中先考慮setv再考慮addv
而在query中要綜合考慮setv和addv.
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int maxnode = 1<<17; int _sum, _min, _max, op, x1, x2, y1, y2, x, v; class IntervalTree { int sumv[maxnode], minv[maxnode], maxv[maxnode], setv[maxnode], addv[maxnode]; // 維護節點o void maintain(int o, int L, int R) { int lc = o*2, rc = o*2+1; if(R > L) { sumv[o] = sumv[lc] + sumv[rc]; minv[o] = min(minv[lc], minv[rc]); maxv[o] = max(maxv[lc], maxv[rc]); } if(setv[o] >= 0) { minv[o] = maxv[o] = setv[o]; sumv[o] = setv[o] * (R-L+1); } if(addv[o]) { minv[o] += addv[o]; maxv[o] += addv[o]; sumv[o] += addv[o] * (R-L+1); } } //標記傳遞 void pushdown(int o) { int lc = o*2, rc = o*2+1; if(setv[o] >= 0) { setv[lc] = setv[rc] = setv[o]; addv[lc] = addv[rc] = 0; setv[o] = -1; // 清楚標記 } if(addv[o]) { addv[lc] += addv[o]; addv[rc] += addv[o]; addv[o] = 0; // Çå³ý±¾½áµã±ê¼Ç } } void update(int o, int L, int R) { int lc = o*2, rc = o*2+1; if(y1 <= L && y2 >= R) { // 在區間內 if(op == 1) addv[o] += v; else { setv[o] = v; addv[o] = 0; } } else { pushdown(o); int M = L + (R-L)/2; if(y1 <= M) update(lc, L, M); else maintain(lc, L, M); if(y2 > M) update(rc, M+1, R); else maintain(rc, M+1, R); } maintain(o, L, R); } void query(int o, int L, int R, int add) { if(setv[o] >= 0) { int v = setv[o] + add + addv[o]; _sum += v * (min(R,y2)-max(L,y1)+1); _min = min(_min, v); _max = max(_max, v); } else if(y1 <= L && y2 >= R) { _sum += sumv[o] + add * (R-L+1); _min = min(_min, minv[o] + add); _max = max(_max, maxv[o] + add); } else { int M = L + (R-L)/2; if(y1 <= M) query(o*2, L, M, add + addv[o]); if(y2 > M) query(o*2+1, M+1, R, add + addv[o]); } } }; const int maxr = 20 + 5; const int INF = 1000000000; IntervalTree tree[maxr]; int main() { int r, c, m; while(scanf("%d%d%d", &r, &c, &m) == 3) { memset(tree, 0, sizeof(tree)); for(x = 1; x <= r; x++) { memset(tree[x].setv, -1, sizeof(tree[x].setv)); tree[x].setv[1] = 0; } while(m--) { scanf("%d%d%d%d%d", &op, &x1, &y1, &x2, &y2); if(op < 3) { scanf("%d", &v); for(x = x1; x <= x2; x++) tree[x].update(1, 1, c); } else { _sum = 0; _min = INF; _max = -INF; for(x = x1; x <= x2; x++) tree[x].query(1, 1, c, 0); printf("%d %d %d\n", _sum, _min, _max); } } } return 0; }
再來看看樹狀陣列的
先來個改點求區間的
看看hdu1161
題目連結:
題目大意:給n個初始資料構建一棵樹狀陣列,然後進行查詢求和等一些列操作。
標準模板題,不解釋。
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
const int MAX=50005;
int N;
class BIT
{
private:
int bit[MAX];
int lowbit(int t)
{
return t&-t;
}
public:
BIT()
{
memset(bit,0,sizeof(bit));
}
int sum(int i)
{
int s=0;
while(i>0)
{
s+=bit[i];
i-=lowbit(i);
}
return s;
}
void add(int i,int v)
{
while(i<=N)
{
bit[i]+=v;
i+=lowbit(i);
}
}
};
int main()
{
int T;
while(cin>>T)
{
for(int t=1;t<=T;t++)
{
printf("Case %d:\n",t);
cin>>N;
BIT tree;
for(int i=1;i<=N;i++)
{
int x;
cin>>x;
tree.add(i,x);
}
char ord[15];
while(scanf("%s",ord)&&strcmp(ord,"End"))
{
int a,b;
scanf("%d%d",&a,&b);
switch(ord[0])
{
case 'Q':
printf("%d\n",tree.sum(b)-tree.sum(a-1));
break;
case 'A':
tree.add(a,b);
break;
case 'S':
tree.add(a,-b);
break;
}
}
}
}
return 0;
}再看一道修改區間,然後單點查詢的
看hdu 1556
N個氣球排成一排,從左到右依次編號為1,2,3....N.每次給定2個整數a b(a <= b),lele便為騎上他的“小飛鴿"牌電動車從氣球a開始到氣球b依次給每個氣球塗一次顏色。但是N次以後lele已經忘記了第I個氣球已經塗過幾次顏色了,你能幫他算出每個氣球被塗過幾次顏色嗎?
這題是修改區間的,單點查詢的,則要注意一點 先對左區間進行操作add(a,1),然後對右邊區間進行操作add(b+1,-1),把不該修改的那部分值再修改回來,即實現了對一個區間的值的修改。然後通過sum(i),即可求點(如果有人問為什麼是sum(i)而不是bit[i]呢?我只能說你太天真了。。。。自己再紙上畫畫就能知道。。。。)
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int MAX=100001;
int N;
class BIT2
{
private:
int bit[MAX];
int lowbit(int t)
{
return t&-t;
}
public:
BIT2()
{
memset(bit,0,sizeof(bit));
}
int add(int i,int v)
{
while(i<=N)
{
bit[i]+=v;
i+=lowbit(i);
}
}
int sum(int i)
{
int s=0;
while(i>0)
{
s+=bit[i];
i-=lowbit(i);
}
return s;
}
};
int main()
{
while(cin>>N&&N)
{
int a,b;
BIT2 tree;
for(int i=1;i<=N;i++)
{
scanf("%d%d",&a,&b);
tree.add(a,1);
tree.add(b+1,-1);
}
for(int i=1;i<=N;i++)
{
if(i!=1) cout<<" ";
printf("%d",tree.sum(i));
}
cout<<endl;
}
return 0;
}再看一道二維的
Hdu1892
跟一維主要的區別
void init()
{
for(int i=1;i<MAX;i++)
for(int j=1;j<MAX;j++)
{
d[i][j]=1;
c[i][j]=lowbit(i)*lowbit(j);
}
}
int sum(int i,int j)
{
int tot=0;
for(int x=i;x>0;x-=lowbit(x))
for(int y=j;y>0;y-=lowbit(y))
{
tot+=c[x][y];
}
return tot;
}
void add(int i,int j,int v)
{
for(int x=i;x<MAX;x+=lowbit(x))
for(int y=j;y<MAX;y+=lowbit(y))
{
c[x][y]+=v;
}
}