圓檢測(續)- RANSAC
繼之前提到的兩種方法之後,這裡再列出基於RANSAC的圓檢測,RANSAC(Random Sample Consensus)隨機抽樣一致性,略不同於霍夫圓變換那種基於投票的策略,這是一種對觀測資料進行最大化模型檢驗的方法。下面來簡單介紹一下它的原理:
1、原理
最小二乘法通常用線上性擬合引數中,但一旦最小二乘法輸入的觀測資料中包含有大量分散的干擾點時,它擬合出來的效果可能並不好,如可能會出現這樣的情況:
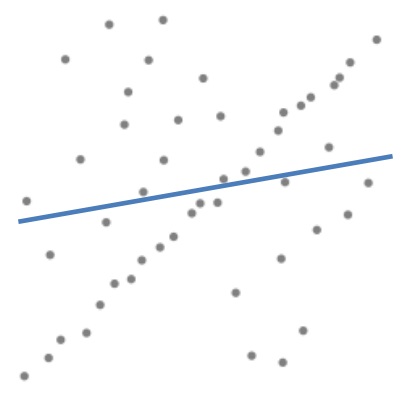
可以看到,擬合出來的直線與期望有效點之間的重合率不高,也就代表著它的代價函式
Ransac的思路是隨機通過幾個點用最小二乘法給出一個假設的直線,然後計算在直線內的inliers和在直線範圍外的outliers。對所有可能的直線中找出inliers數目最多的那個,也就能找到最好的直線。
演算法步驟:
(1) 隨機地抽取出所需要數目的點去擬合模型:
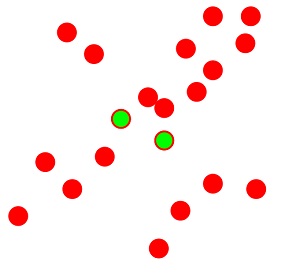
綠色的點代表取樣的點
(2)用樣本求出模型引數:
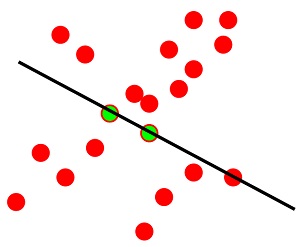
(3)在設定好直線的閾值範圍中區分出inliers和outliers,並求內點佔觀測資料的比:
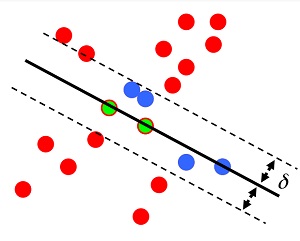
重複步驟1-3直到找出置信度最高的模型
RANSAC幾點要注意的:
① 只有outliers%<50%時,得到的模型才是有保證的。
②inliers的閾值
③ 重複1-3步驟的次數跟模型的outliers佔比和我們所需要多高的置信度有關,可以用下面公式表示:
其中,S是所需最小試驗的次數,P是置信度,p是inliers佔的百分比數,k是隨機取樣的數目。
2、實際例子
這裡用網友Micka的程式碼來舉例:
#include <opencv2/opencv.hpp>
#include <ctime>
float verifyCircle(cv::Mat dt, cv::Point2f center, float radius, std::vector<cv::Point2f> & inlierSet)
{
unsigned int counter = 0;
unsigned 他的思路是:
1. 用Canny提取邊緣點, 用distanceTransform得到距離邊緣點的距離圖;
2. 隨機抽取三個不同的點解方程,三個方程三個未知數,有解;
3. 將2得到的圓周上的點與1中對應位置的點進行比較,看是否屬於inliers,隨後輸出百分比;
4. 找出最大百分比對應的圓就是RANSAC得到的圓。
3、比較霍夫變換跟RANSAC:
魯棒性來說,霍夫變換要穩定一點;
速度來說,霍夫變換要快,而且其所需時間變化不大,100ms左右能夠完成;
RANSAC跟HoughTranform的引數調節都很麻煩,相對來說,霍夫變換更加簡單一點;
RANSAC擬合的程度可能會更高,但受到outliers%<50%這個條件限制。
所以綜合來說,HoughTransform的應用更廣,效率更高,某些情況下,它不能很好地找到合理的圓,這時可以將RANSAC加進去進行優化,可能精度會高很多。
參考資料:
