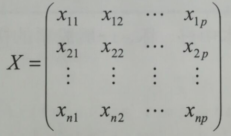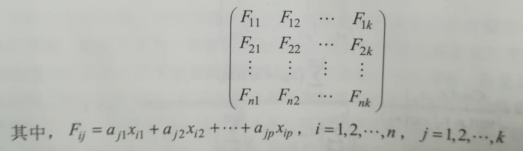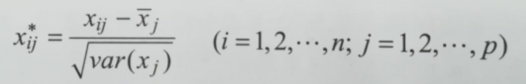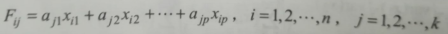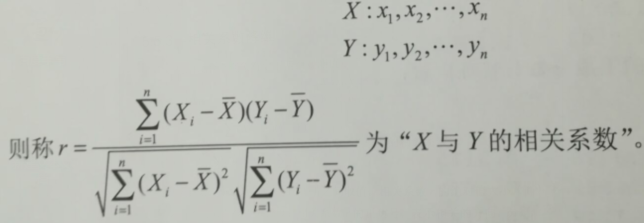１.４資料降維

在分析多個變數時發現它們中有一定的相關性。有一種方法將多個變數綜合成少數幾個相互無關的代表性變數來代替原來的變數，這就是資料降維，可以考慮主成分分析法。

1)、主成分分析法（PCA）

1、基本思想

（1）如果將選取的第一個線性組合即第一個綜合變數記為F1，自然希望它竟可能多的反映原來的變數資訊。（這裡的“資訊”用方差來測量，即希望Var（F1）方差函式越大，表示F1包含的資訊愈多），因此在所有的線性組合中所選取的F1應該是方差最大的，故稱F1為第一主成分。

（2）如果第一主成分不足以代表原來P個變數的資訊，在考慮選取F2（即第二個線性組合）,為了有效的反映原來的資訊，F1已有的資訊就不需要出現在F2中（即用數學表示式Cov函式為

統計學協方差：Cov（F1 , F2）=0），稱F2為第二主成分。

（3）以此類推可以構造第三、第四。。。。。第p個主成分。

2、PCA步驟

觀測資料矩陣：

（1）、對原始資料進行標準化處理。

變數：i：矩陣的行，j：矩陣的列；~X j：表示 j 列的均值（期望）var（）函式：方差

（2）、計算樣本相關係數矩陣。

（3）、計算相關係數矩陣R的特徵值和相應的特徵變數。

這裡不在論述，不懂得看看線性代數，這裡有matlab的

（4）、選著重要的成分，並寫出主成分表示式。

①主成分分析可以得到P個主成分。但是，由於各個主成分的方差是遞減的，包含的資訊量也是減少的，所以實際分析時，一般不是選取P個主成分，而是根據各個主成分累計貢獻率的大小選取前K個主成分。但要要求累計貢獻率達到85%以上，這樣才能保證綜合變數包括原始變數的絕大多數資訊。

②貢獻率：某個主成分的方差佔全部方差的比重，即某個特徵值佔全部特徵值合計的比重。

③接下來要進行綜合變數（即主成分變數）在一起應賦予怎樣的實際含意解釋，這要結合具體的實際問題和專業給出合理的解釋，進而才能達到深刻分析的目的。

④一般而言，這個解釋是根據主成分表示式的係數結合定性分析來進行的。

⑤主成分是原本變數的線性組合，在這個線性組合中各變數的係數有大有小，有正有負，有的大小相當，因而不能簡單地認為這個主成分是某個變數的的屬性的作用。

⑥線性組合中各變數的絕對值大者表明該主成分主要綜合了絕對值大的變數，有幾個變數係數大小相當時，應該認為這一主成分是這幾個變數的總和。

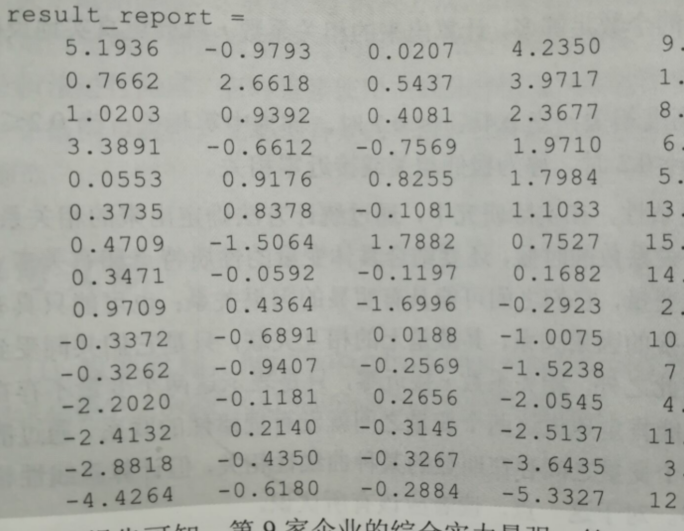
（5）、計算主成分得分。

根據標準化的原始資料，按著這個樣品，分別代入主成分表示式，就可以得到各主成分下的各個樣品的新資料（即主成分得分）。

（6）、依據主成分得分的資料，進一步對問題進行後續的分析和建模。

後續的分析和建模常見的形式：主成分迴歸，變數子集合的選擇，綜合評價等。

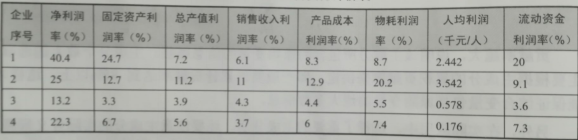
3、PCA例項

由上圖可知：15個企業進行綜合例項排序。這裡有8個指標，但是他們間的關聯關係並不是太明確，且各指標數值的數量級也有差異，為此這裡首先借助PCA方法對指標體系進行降維處理。然後根據PCA打分結果實現對企業的綜合例項排序。

這裡是用matlab進行編碼的

（1）資料匯入及處理

程式：

引數：xlsread（）：將表格匯入並賦值給A

（2）資料標準化處理

程式：

引數：A：矩陣，a：矩陣的行數，b：矩陣列數，SA：標準化後矩陣，mean（）函式：均值函式，std（）函式：方差函式

相關公式：

x*：標準化矩陣，x：原始矩陣，~x j：表示列均值，var（）函式：方差函式

（3）計算相關係數矩陣的特徵值和特徵向量    

程式：

引數：CM：相關係數矩陣，SA：標準化後矩陣，V：相關係數的特徵向量，D：相關係數的特徵值，corrcoef（）函式：計算相關係數，eig（）函式：計算特徵值和特徵向量

相關公式：

r：標準化矩陣的相關係數，cov（）函式：協方差函式，var（）函式：方差

（4）計算主成分

①計算貢獻率和累計貢獻率

程式：

引數：b：矩陣列數，D：相關係數的特徵值，DS：關於特徵值、貢獻率和累計貢獻率的矩陣，sum（）函式：求和函式

相關公式：，   累計貢獻率G(m)   

引數λ：為相關係數的特徵值

結果：DS第一列為特徵值，並且排過序，第二列為貢獻率，第三列為累計貢獻率

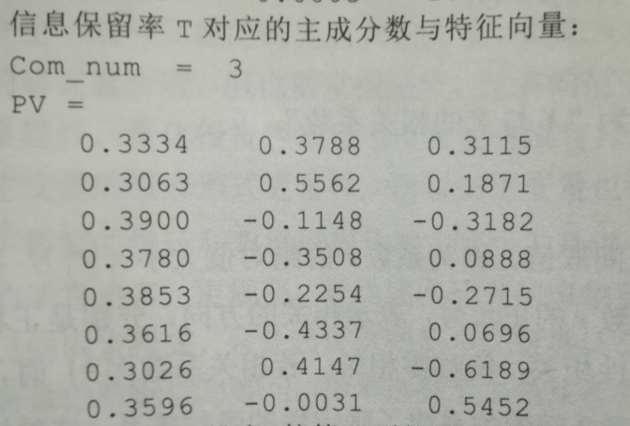
②選擇的主成分以及對應的的特徵向量

程式：

引數：T：主成分保留率，b：標準化矩陣的列，Com_num：選取的主成分數量；V：相關係數矩陣的的特徵向量；PV：選取的主成分對應的特徵向量

結果：

（5）計算各評價物件的主成分得分

程式：

引數：new_score ：選取的主成分得分矩陣，SA：標準化之後的X矩陣 ，PV：選取的主成分對應的特徵向量，total_score：選取的主成分的和以及企業編號，result_report：選取的主成分和總分以及編號，sum（）函式：求和，sortrows（）函式：排序

相關公式：

F：主成分得分，a：相關係數特徵向量，x：標準化矩陣裡面的數值

結果：result_report：1,2,3,列是各主成分得分；4列是前三列的和，是各主成分的總分；5列為企業編號

從上面報告可知，第9綜合例項最強，第12最弱

2）、相關係數降維

定義：X，Y 為兩組觀測資料

   

①相關係數用 r 表示，與PCA裡面的相關係數一樣，r 在-1和+1之間取值。

②相關係數 r 的絕對值大小|r|，表示兩個變數之間的直線相關強度

③相關係數 r 的正負號，表示相關的方向，分別為正相關和負相關

④相關係數 r = 0，則稱零線性相關，簡稱零相關

⑤相關係數 |r| = 1，則表示兩個變數完全相關，這時兩個變數有確定的函式關係。

⑥相關係數 0.7 < |r| < 1，稱高度相關；0.4 < |r| < 0.7，稱中等相關；0.2 < |r| < 0.4，稱低度相關；|r| < 0.2，稱極低相關或近零相關

⑦兩個高度相關的變數，要進行分析關係，他們之間可能具有明顯的因果關係，也可能只具有部分因果關係，還可能沒有直接的因果關係，其數量上的 相關聯，只是他們共同受到第三個變數所支配的結果

⑧相關係數 r接近零，只能表示兩個變數不存在明顯的線性相關，但不能肯定的說明兩個變數之間沒有規律性的聯絡，根據散點圖，可以看到他們有可能會有某種曲線相關，但是不是直線型相關，其 r 值往往接近零。