實現最大流有好幾種演算法，比如Dinic或者ISAP演算法，Edmonds-Karp只是其中最好理解的一種演算法，它的實現要運用到增廣路與BFS，當然也可以用DFS，但效率太低。網路流這東西是用來求從s點到t點（起點為s，終點為t）的流量問題，因為類似網路資料傳輸，所以叫做網路流。

        最大流說簡單點就是使從s到t的流量最大。這玩意兒需要注意三個事實（起點為s，終點為t）：

        BFS是普及組必須掌握的，就不多講了。以下是一些基本知識（有些東西在後面會簡寫，所以注意一下）：

        1.容量（c），每條邊最大運輸量。

        2.流量（f），當前用了的運輸量。

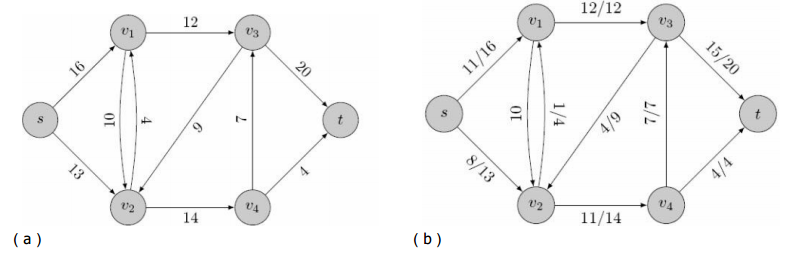
        3.殘量網路，即每一條路上容量與流量之差，必須為正數，注意，若a->b的c為16，f為10，在殘量網路中a->b為6還有一條邊，b->a為10，有兩條邊！因為可以當做b->a為容量0，流量-11。例如圖（a）的殘量網路為圖（b）（前一個數為流量，後一個數為容量）。

        4.增廣路，每次在圖中找到一條滿足上述基本事實的一條從s到t的路（這裡用BFS找），這條路上貢獻的流量就是其最小殘量，每次找到一條路，就讓答案加上最小殘量，當沒有增廣路時，可以證明答案即為最優。

        下面貼上程式碼：

#include<queue>
#include<cstdio>
#include<vector>
#include<cstring>
#define maxn 1005
#define INF 2147483647
using namespace std;
int read(){
	int ret=0,f=1;char  ch=getchar();
	while(ch<'0'||ch>'9') {if(ch=='-')f=-f;ch=getchar();}
	while(ch>='0'&&ch<='9') ret=ret*10+ch-'0',ch=getchar();
	return ret*f;
}
struct Edge{//用來維護每條邊的資訊 
	int from,to,cap,flow;
	Edge(int u,int v,int c,int f):from(u),to(v),cap(c),flow(f){}
};
struct EdmondsKarp{
	int n,m,s,t;//n:點數，m:邊數，s:起點,t:終點 
	vector<Edge> edges;//邊數開兩倍（還有反向網路），這裡偷一下懶 
	vector<int> G[maxn];//領接表，G[i][j]表示點i到延伸出去的第j條邊在edges中的位置 
	int a[maxn];//最小殘量，用以增廣 
	int p[maxn];//p[i]表示到達節點i的那條邊的編號，因為每次增廣只增廣一條路徑，所以不用開二維 
	void init(){//不多說，初始化 
		n=read();m=read();s=read();t=read();
		for(int i=0;i<n;i++) G[i].clear();
		edges.clear();
		for(int i=1;i<=m;i++){
			int from=read(),to=read(),cap=read();
			edges.push_back(Edge(from,to,cap,0));
			edges.push_back(Edge(to,from,0,0));//反向網路 
			int k=edges.size();
			G[from].push_back(k-2);
			G[from].push_back(k-1);  
		}
	}
	int Maxflow(){
		int ret=0;
		while(1){
			memset(a,0,sizeof(a));
			queue<int> Q;//先進先出的佇列 
			Q.push(s);
			a[s]=INF;
			while(!Q.empty()){//裡面就是在BFS 
				int x=Q.front();//取隊首 
				Q.pop();
				for(int i=0;i<G[x].size();i++){
					Edge& e=edges[G[x][i]];
					if(!a[e.to]/*判環*/&&e.cap>e.flow){
						p[e.to]=G[x][i];//記住回去的路 
						a[e.to]=min(a[x],e.cap-e.flow);//去最小殘量 
						Q.push(e.to);
					}
				}
				if(a[t]) break;//此條路已到達t 
			} 
			if(!a[t]) break;//沒有增廣路時，即為最大流 
			for(int u=t;u!=s;u=edges[p[u]].from){//藉助p陣列倒回去給此次找到的增廣路上的每條路的流量都加上最小殘量a[t] 
				edges[p[u]].flow+=a[t];
				edges[p[u]^1].flow-=a[t];//反向網路也要減掉a[t] 
			}
			ret+=a[t];//答案加上最小殘量a[t] 
		}
		return ret;
	}
}ans;
int main(){
	freopen("ls.in","r",stdin);
	ans.init();
	printf("%d",ans.Maxflow());
	return 0;
}
 

感謝《演算法競賽 入門經典》的圖