圖論09—MATLAB自帶最短路函式
一、寫出稀疏矩陣
- 方法一 a.起點為行,終點為列,寫出行向量R和列向量C
- 方法二 a.寫出權值矩陣或已知權值矩陣W
c.當G(i,j)==inf時刪除,即構成最終的稀疏矩陣
二、最短路演算法命令格式
view(biograph(G));
graphallshortestpath(G);
[dist path]=graphshortest(G,s,t);
[M,F,C]=graphmaxflow(G,s,t);
例:
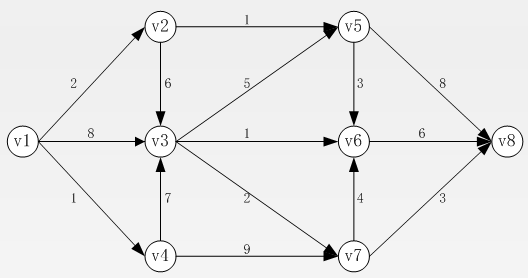
(1)構造下圖的稀疏矩陣(注意方向)。
(2)使用MATLAB依據稀疏矩陣畫出該圖的結構圖。
(3)求出各點之間的最短距離。
(4)求出點v1到點v8的最短距離和路徑,並在拓撲圖中用紅色標記,路徑加粗顯示。
(5)若用邊權代表通過能力(假設),求出最大流的分配方案。
解:(1)稀疏矩陣
方法一:
>> R=[1 1 2 4 1 2 3 3 5 7 3 4 5 6 7];
>> C=[2 3 3 3 4 5 5 6 6 6 7 7 8 8 8];
>>W=[2 8 6 7 1 1 5 1 3 4 2 9 8 6 3];
>> G1=sparse(R,C,W)
G1 =
(1,2) 2
(1,3) 8
(2,3) 6
(4,3) 7
(1,4) 1
(2,5) 1
(3,5) 5
(3,6) 1
(5,6) 3
(7,6) 4
(3,7) 2
(4,7) 9
(5,8) 8
(6,8) 6
(7,8) 3
即該圖的稀疏矩陣為G1.
方法二:
>> W =[
0 2 8 1 Inf Inf Inf Inf
Inf 0 6 Inf 1 Inf Inf Inf
Inf Inf 0 Inf 5 1 2 Inf
Inf Inf 7 0 Inf Inf 9 Inf
Inf Inf Inf Inf 0 3 Inf 8
Inf Inf Inf Inf Inf 0 Inf 6
Inf Inf Inf Inf Inf 4 0 3
Inf Inf Inf Inf Inf Inf Inf Inf];
>> G=sparse(W);
>> for i=1:length(W)
for j=1:length(W)
if G(i,j)==inf
G(i,j)=0;
end
end
end
>> G2=G
G2 =
(1,2) 2
(1,3) 8
(2,3) 6
(4,3) 7
(1,4) 1
(2,5) 1
(3,5) 5
(3,6) 1
(5,6) 3
(7,6) 4
(3,7) 2
(4,7) 9
(5,8) 8
(6,8) 6
(7,8) 3
即稀疏矩陣為G2,顯然G1=G2.
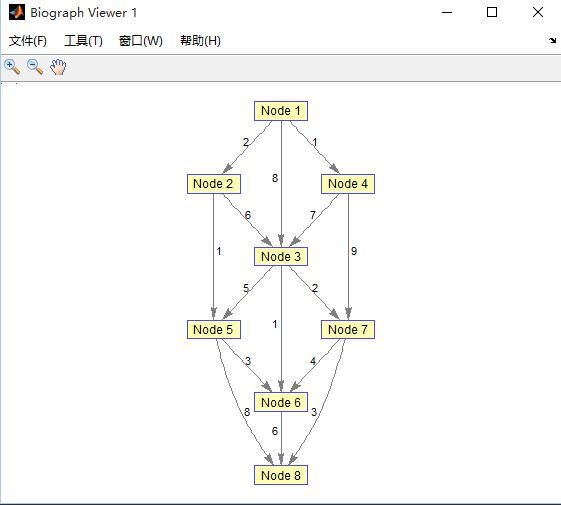
(2)結構圖
>> view(biograph(G2,[],'ShowW','ON'))
(3)任意點之間的最短距離
>> graphallshortestpaths(G2)
ans =
0 2 8 1 3 6 10 11
Inf 0 6 Inf 1 4 8 9
Inf Inf 0 Inf 5 1 2 5
Inf Inf 7 0 12 8 9 12
Inf Inf Inf Inf 0 3 Inf 8
Inf Inf Inf Inf Inf 0 Inf 6
Inf Inf Inf Inf Inf 4 0 3
Inf Inf Inf Inf Inf Inf Inf 0
說明:第1行為點V1到其他點的距離,到v2為2,v3為8……v8為11。第i行為vi到其他點的距離向量。
(4)求v1到v8的最短距離和路徑並畫圖顯示。
[dist path]=graphshortestpath(G2,1,8)
dist =
11
path =
1 2 5 8
即最短距離為11,路徑為1->2->5->8.
>> h=view(biograph(G2,[],'showW','on'));
>> edges=getedgesbynodeid(h,get(h.Nodes(path),'ID'));
>> set(h.Nodes(path),'color',[1 0 0])
>> set(edges,'LineColor',[1 0 0])
>> set(edges,'LineWidth',1.5)
%則圖片更改為:
(5)最大流
>> [M,F,C]=graphmaxflow(G2,1,8)
M =
10
F =
(1,2) 2
(1,3) 7
(2,3) 1
(1,4) 1
(2,5) 1
(3,5) 5
(3,6) 1
(3,7) 2
(4,7) 1
(5,8) 6
(6,8) 1
(7,8) 3
C =
1 1 1 0 0 0 0 0
>> m=view(biograph(F,[],'showW','ON'))
即最大流為10,方案如上圖。最小割為1 2 3,如下圖.